文章目录
- 前言
- 一、矩阵连乘问题
- 1、问题描述
- 2、完全加括号
- 3、问题分析
- 4、最优子结构性质
- 5、状态表示和递推方程
- 6、自问题个数和求解顺序
- 二、计算最优值示例
- 1、问题描述
- 2、计算最优值示例*****
- 3、构造最优解
- 4、算法实现
- 三、基本要素-最优子结构
- 四、基本要素-重叠子问题
- 五、递归方法
- 六、备忘录方法
- 七、动态规划算法设计的步骤
前言
- 三部曲如下三步:
- 基本原则:“空间换时间” 存储重复子问题的解,减少运算时间
- 底层运算:“表格操作” 用表格存储子问题的解
- 实现路线:“子问题划分、自底向上求解” 利用表格中存储的子问题的解,求上一层子问题的解。
一、矩阵连乘问题
1、问题描述


2、完全加括号
矩阵连乘计算次序 可以用 加括号的方式 来确定。特别的,完全加括号的矩阵连乘积可递归地定义为:
- 单个矩阵是完全加括号的
- 矩阵连乘积 A 是完全加括号的,则 A 可示为2个完全加括号的矩阵连乘积 B 和 C 的乘积并加括号,即 A=(BC)

3、问题分析
给定n个矩阵𝐴1,⋯, 𝐴𝑛,其中第i个矩阵的维度为𝑝(𝑖−1)×𝑝𝑖,以及它们的一个完全加括号方案:
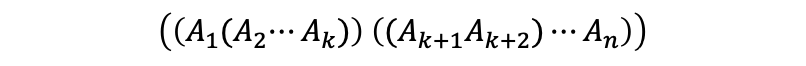


4、最优子结构性质
构建原问题最优解 与 子问题最优解之间的关系:

5、状态表示和递推方程

6、自问题个数和求解顺序

二、计算最优值示例
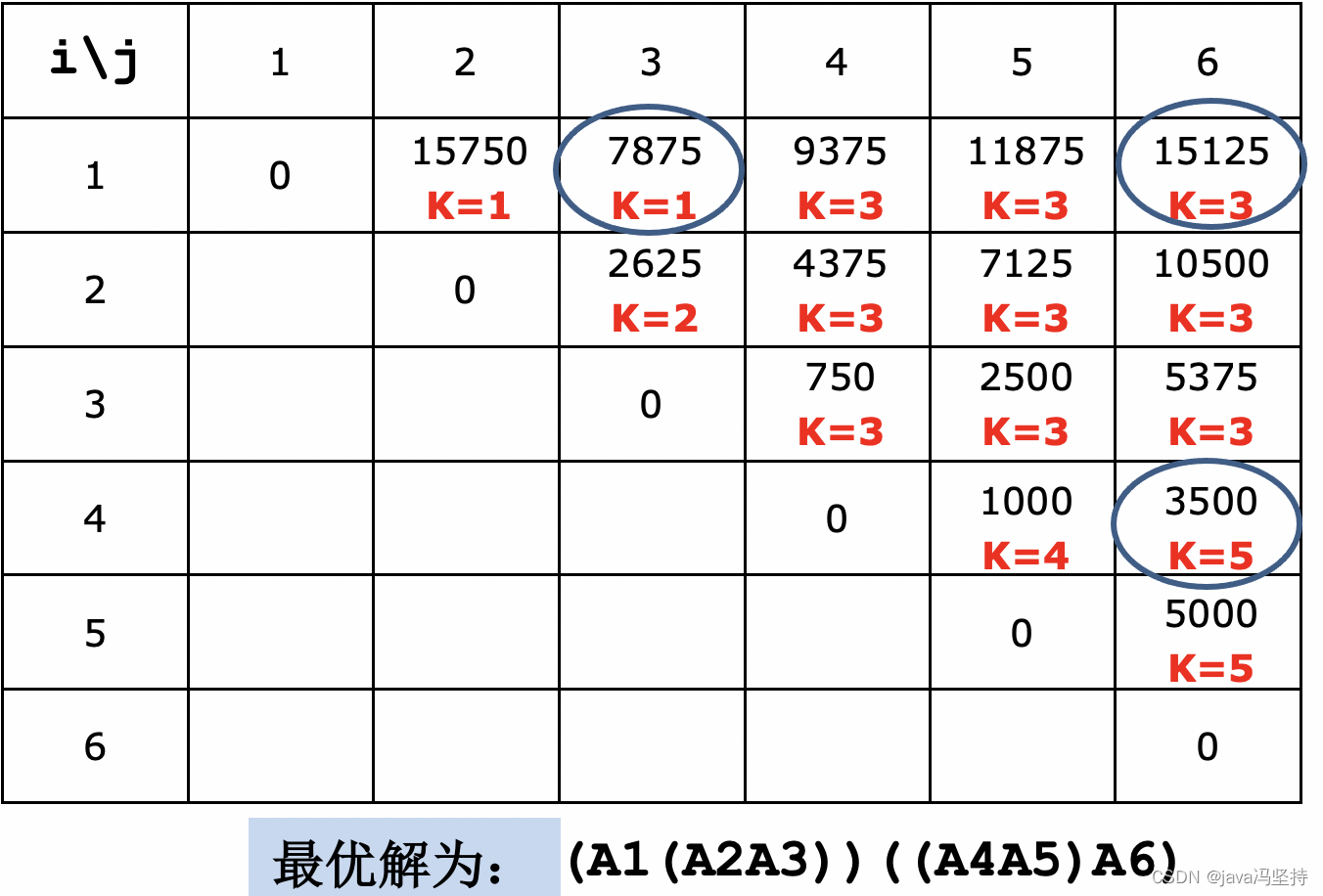
1、问题描述
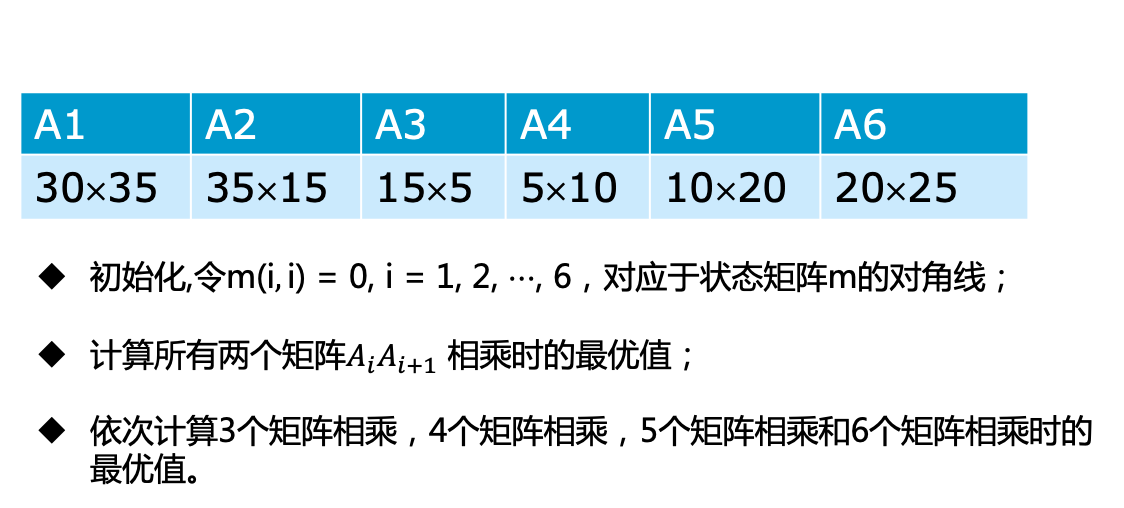
2、计算最优值示例*****

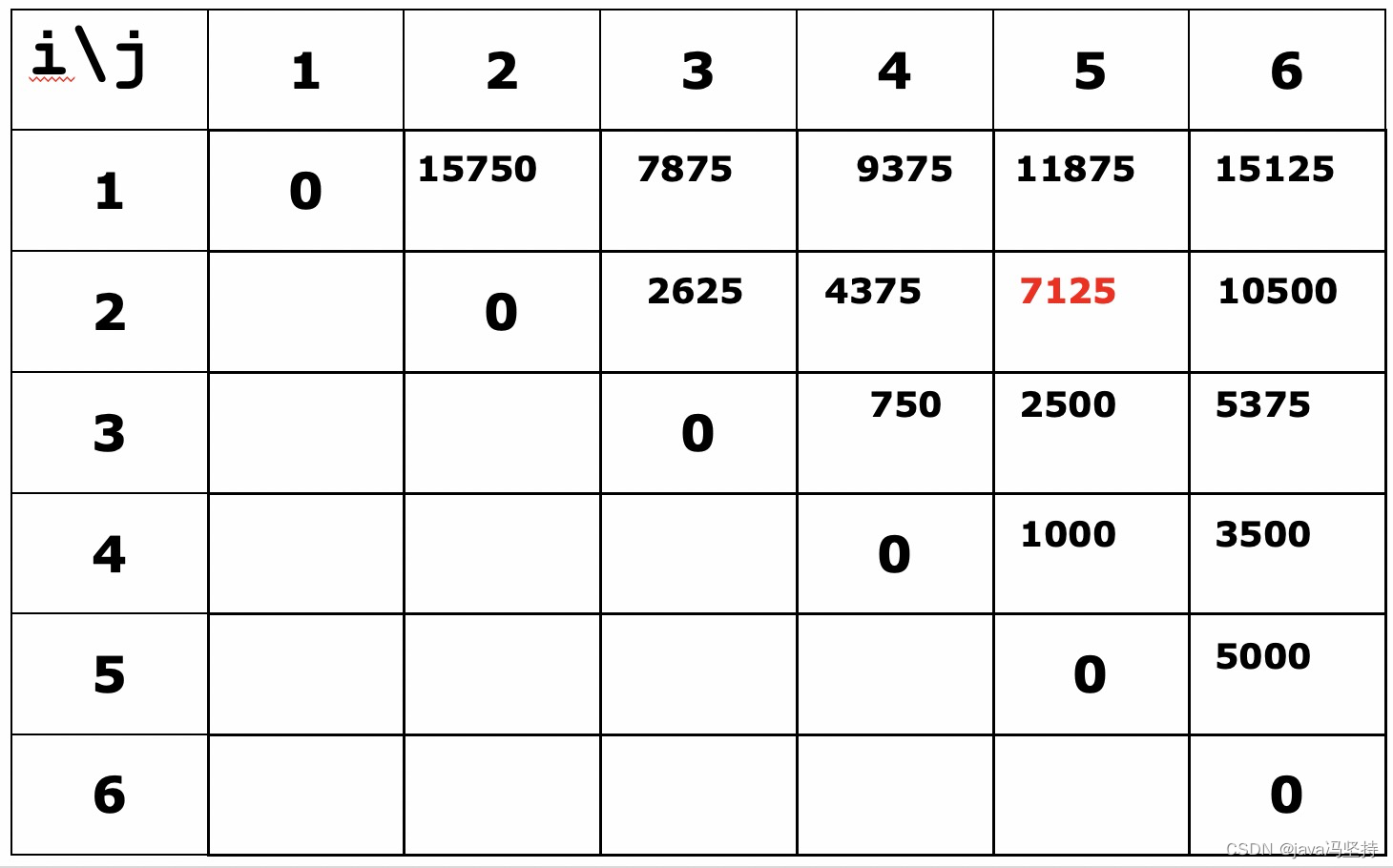
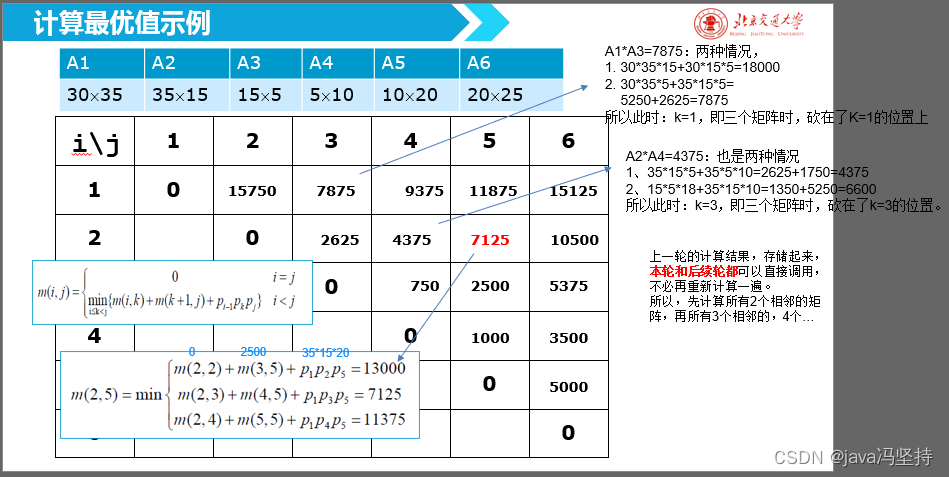
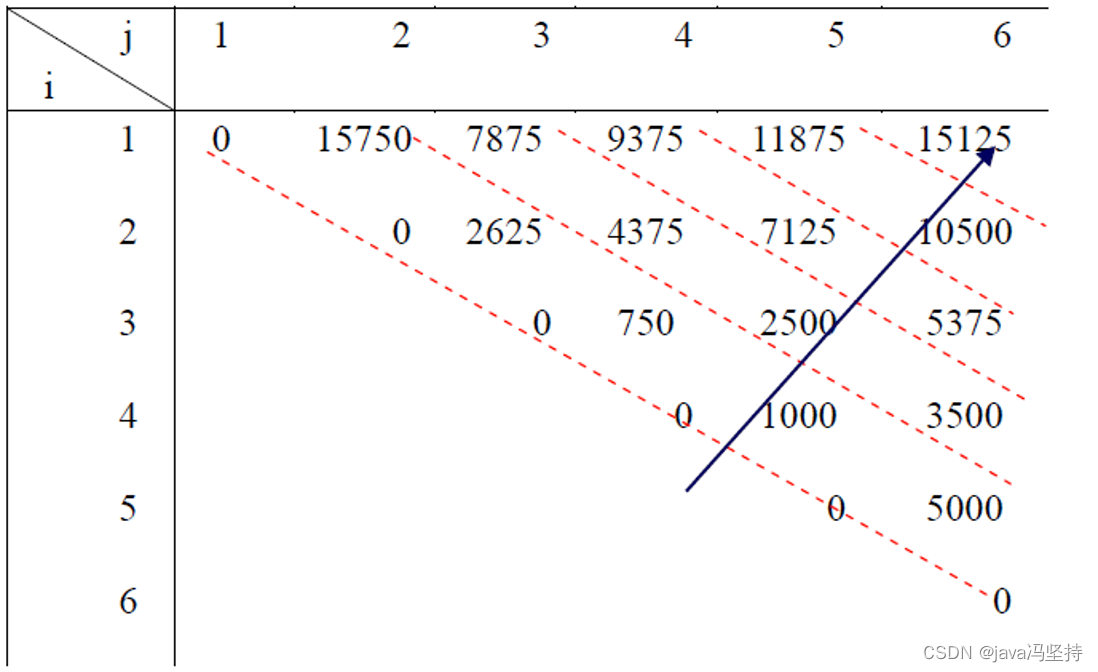
按以下顺序计算:
- 第一次计算(遍历):
m(1,2)=30 * 35 * 15 = 15750
m(2,3)=35 * 15 * 5 = 2625
m(3,4)=15 * 5 * 10 = 750
m(4,5)=5 * 10 * 20 = 1000
m(5,6)=10 * 20 * 25 = 5000 - 第二次计算(遍历)
m(1,3)=7875时,有两种情况,k = 1 或者 k =2 时,(下面的数据就可以使用上面算法的,这就是自底向上)
k=1时,m(1,1)+m(2,3)+30 * 35 * 5= 7875
k=2时,m(1,2)+m(3,3)+30 * 15 * 5= 23000
最小的值为7875,m(2,4)=4375时,有两种情况,k = 2 或者k =3 时,(同上)
k = 2时,m(2,2)+m(3,4)+35 * 15 * 10 = 6000
k = 3时,m(2,3)+m(3,3)+35 * 5 * 10 = 4375
最小的值为 4375- 后面同上计算,依次是:
m(3,5)=2500,k=3 或者 k=4m(4,6)=3500,k=4 或者 k=5
- 第三次计算(遍历)
m(1,4)=9375时,k 有三次情况,k=1,k=2,k=3,(同上)
k=1时,m(1,1)+m(2,4)+30 * 35 * 10 = 14875
k=2时,m(1,2)+m(3,4)+30 * 15 * 10 = 21000
k=3时,m(1,3)+m(4,4)+30 * 5 * 10 = 9375m(2,5)=7125时,k 有三次情况,k=2,k=3,k=4
k = 2,m(2,2)+m(3,5)+35 * 15 * 20 = 13000
k = 3,m(2,3)+m(4,5)+35 * 5 * 20 = 7125
k = 4,m(2,4)+m(5,5)+35 * 10 * 20 = 11375m(3,6)=5375
- 第四次计算(遍历)
m(1,5)=11875时,k 有四次情况,k=1,k=2,k=3,k=4,(同上)
k=1时,m(1,1)+m(2,5)+30 * 35 * 20 = 28125
k=2时,m(1,2)+m(3,5)+30 * 15 * 20 = 27250
k=3时,m(1,3)+m(4,5)+30 * 5 * 20 = 11875
k=4时,m(1,4)+m(5,5)+30 * 10 * 20 = 15375m(2,6)=10500
- 第五次计算(遍历)
m(1,6)= 15125时,k 有五次情况,k=12345,(同上)
k = 1时,m(1,1)+m(2,6)+30 * 35 * 25 = 36750
k = 2时,m(1,2)+m(3,6)+30 * 15 * 25 = 34250
k = 3时,m(1,3)+m(4,6)+30 * 5 * 25 = 15125
k = 4时,m(1,4)+m(5,6)+30 * 10 * 25 = 21875
k = 5时,m(1,5)+m(5,5)+30 * 20 * 25 = 26875
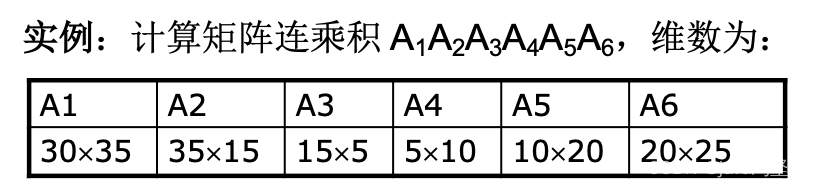
3、构造最优解

4、算法实现
import java.util.Scanner;
/**
* DP 算法之 矩阵连乘
*/
public class Main {
public static long[][] memoTable; // 存放局部最优值
public static int[][] bestK ; // 存放 划括号k 的位置
public static int[] dim ; // 存放矩阵的值
public static int matrixNum; // 二位矩阵 的维度
/**
* 自底向上地计算最优值,结果保存在全局变量memoTable和bestK中
* @param matrixNum
* @return
*/
static long MatrixChain(int matrixNum) {
int i,j,len,k;
for(i=1; i<=matrixNum; i++) //单个矩阵的情形,定义数乘次数为0
memoTable[i][i] = 0;
for(len=2; len<=matrixNum; len++){ //计算长度为len的矩阵链最优值
for(i=1; i<=matrixNum-len+1; i++) { //矩阵链的开始矩阵下标
j = i+len-1; //矩阵链的结束矩阵下标
memoTable[i][j] = 100000000; //预定义的一个充分大数
for(k=i; k<j; k++) { //枚举划分位置
long ans = memoTable[i][k] + memoTable[k+1][j] +
dim[i-1]*dim[k]*dim[j];
if (ans < memoTable[i][j]){ //更新最优信息
bestK[i][j] = k;
memoTable[i][j] = ans;
}
}//end of for k
}//end of for i
}//end of for len
return memoTable[1][matrixNum];
}
/**
* 递归构造最优解
* @param i
* @param j
* @param bestK
* @return
*/
public static String traceback(int i,int j,int[][] bestK) {
if(i==j) {
return String.format("A%s", i);
}
if(i==j-1){
return String.format("A%sA%s", i, j);
}
int position = bestK[i][j];
StringBuilder sb = new StringBuilder();
if(i!=position) {
sb.append("(");
}
sb.append(traceback(i, position, bestK));
if(i!=position) {
sb.append(")");
}
if(position+1!=j) {
sb.append("(");
}
sb.append(traceback(position+1, j, bestK));
if(position+1!=j) {
sb.append(")");
}
return sb.toString();
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
System.out.println("请输入矩阵的个数:");
matrixNum = in.nextInt();
System.out.println("请输入矩阵的行数和列数:");
dim = new int[matrixNum+1];
for(int i = 0;i <= matrixNum;i++) {
dim[i] = in.nextInt();
}
memoTable = new long[matrixNum+1][matrixNum+1];
bestK = new int[matrixNum+1][matrixNum+1];
long min = MatrixChain(matrixNum);
System.out.println("矩阵连乘的最小次数是:" + min);
System.out.println(String.format("矩阵的连乘次序:%s", traceback(1, matrixNum, bestK)));
}
}
三、基本要素-最优子结构
- 最优子结构性质,通俗地讲就是问题的最优解包含其子问题的最优解。也就是说,如果把问题的最优解分解(比如划分为两个或者多个部分,或者删除第一个或者最后一个分量),得到一个子解,那么这个
子解是其相应子问题的最优解。

- 最优子结构性质隐含了问题最优解和子问题最优解之间的一种递推关系。它是动态规划的基础,递推方程是最优子结构性质的体现。
- 在分析问题的最优子结构性质时,人们一般采用
反证法:首先假设由问题最优解S导出的子问题的解不是最优的,然后再推导在这个假设下可构造出比S更好的解 S’,从而得到矛盾。
四、基本要素-重叠子问题
- 递归算法求解问题时,每次产生的子问题并不总是新问题,有些子问题被反复计算多次。这种性质称为
子问题的重叠性质。 - 动态规划算法,
对每一个子问题只解一次,而后将其解保存在一个表格中,当再次需要解此子问题时,只是简单地用常数时间查看一下结果。 - 通常不同的子问题个数随问题的大小呈
多项式增长。因此用动态规划算法只需要多项式时间,从而获得较高的解题效率。 【降低复杂度不是本章的目标了!!】
五、递归方法
long MatrixChain(int i, int j){
if (i == j) {//单个矩阵的情形
memoTable[i][j] = 0;
return 0;
}
long ans, min = 100000000;//预定义的一个充分大数
for (int k=i; k<j; k++) {
ans = MatrixChain(i,k) + MatrixChain(k+1,j)
+ dim[i-1]*dim[k]*dim[j]; //递归计算
if (ans < min) {
min = ans;
}
}
return min; }
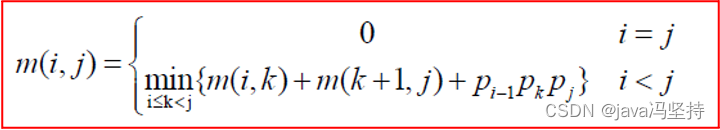
六、备忘录方法

//递归调用前用 memset(memoTable,-1,sizeof(memoTable))初始化备忘录表为-1
long MatrixChainMemo(int i,int j){
if (memoTable[i][j] != -1)
return memoTable[i][j]; //备忘录表中有答案,则跳出递归调用过程
if (i == j) {//单个矩阵的情形
memoTable[i][j] = 0;
return 0;
}
long ans,max = 100000000;//预定义的一个充分大数
for (int k=i; k<j; k++) {
ans = MatrixChainMemo(i,k)+MatrixChainMemo(k+1,j)
+dim[i-1]*dim[k]*dim[j]; //递归计算
if (ans < max) {
bestK[i][j]=k;
max = ans;
}
}
memoTable[i][j] = max; //用递归执行结果更新备忘录表
return max;
}
七、动态规划算法设计的步骤
- 分析最优解的性质,并刻划其
最优子结构特征; - 确定
状态表示S(x~1~,x~2~,…)和状态递推方程,递归地定义最优值; - 确定
状态转移顺序,以自底向上的方式计算出最优值;(从最小问题计算起,保存最优子结果,在计算更大的问题时就可以调用之) - 根据计算最优值时得到的信息,
构造最优解。






![[附源码]java毕业设计小型医院药品及门诊管理](https://img-blog.csdnimg.cn/22827a1459114e5b82245c8415b7f4a4.png)
