目录
一.队列.栈顺序表总结
二.猫狗问题
三.股票价格跨度
四.二叉树的初始化
1.获取树中节点的个数
1.遍历思路
2.子问题思路
2.叶子节点个数
3.获取第K层节点的个数
4.获取二叉树的高度
6.判断一棵树是不是完全二叉树
一.队列.栈顺序表总结
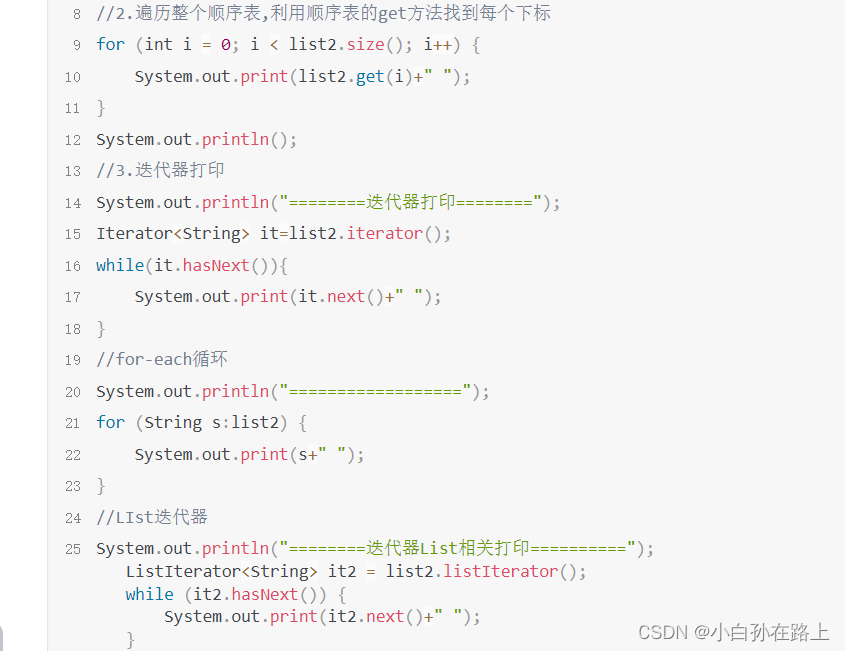


1.顺序表和栈的底层都是动态数组
2.队列的底层是链表,如果继承Queue就是普通队列.如果继承Dueue就是双端链表
队列一般使用offer添加,,poll弹出.peek查看top
3.循环队列的底层也是数组
二.猫狗问题

这道题的思路就是构建两个队列
一个放进入收容所的动物队列
一个是放收养动物的队列.

然后因为这是二维数组,直接构建循环对每一组进行遍历
![]()
构建Switchcase语句对二维数组的每一组的第一个元素进行判断根据题意
如果是1,就把这一组的第二个元素放进list.
如果是2
那么就进入收养程序
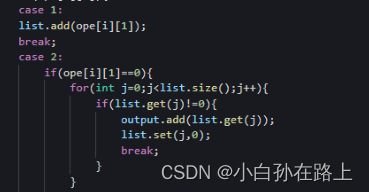
如果是数组第二个元素是0 根据题意就是第一个元素,那么就开始遍历收养的队列,碰到不是0的就放入收养的队列,再把这个下标的元素设为0表示已经被收养然后就可以跳出循环
因为题目只要首次收养的
如果第二个元素不是0.那么就表示是有条件的,要么是大于0的狗要么是大于0的猫.那就还要建立两种判断条件,根据上面的一样,找到一个满足条件的并设置为0
直到数组遍历完.就可以返回收养的队列了
import java.util.*;
public class CatDogAsylum {
public ArrayList<Integer> asylum(int[][] ope) {
// write code here
ArrayList<Integer> input=new ArrayList<>();
ArrayList<Integer> onput=new ArrayList<>();
for(int i=0;i<ope.length;i++){
switch(ope[i][0]){
case 1:
input.add(ope[i][1]);
break;
case 2:
if(ope[i][1]==0){
for(int j=0;j<input.size();j++){
if(input.get(j)!=0){
onput.add(input.get(j));
input.set(j,0);
break;
}
}
}else if(ope[i][1]>0){
for(int j=0;j<input.size();j++){
if(input.get(j)>0){
onput.add(input.get(j));
input.set(j,0);
break;
}
}
}else{
for(int j=0;j<input.size();j++){
if(input.get(j)<0){
onput.add(input.get(j));
input.set(j,0);
break;
}
}
}
break;
}
}
return onput;
}
}三.股票价格跨度

构建两个栈
一个正常放入数值
还有一个放入跨度的大小
设w为1
因为根据题意就算是第一天也是1
看放入的值有没有比栈顶元素大.如果大就让w+w栈弹出的元素.并让价格栈也弹出,构建循环,直到价格栈的栈顶大于放入的值,
然后把循环后的w放入w栈
最后返回w
class StockSpanner {
Stack<Integer> prices;
Stack<Integer> weight;
public StockSpanner() {
prices=new Stack<>();
weight=new Stack<>();
}
public int next(int price) {
int w=1;
while(!prices.isEmpty()&&price>=prices.peek()){
prices.pop();
w+=weight.pop();
}
prices.push(price);
weight.push(w);
return weight.peek();
}
}四.二叉树的初始化
1.获取树中节点的个数
1.遍历思路
遍历二叉树,如果是节点,看是否是空的,不是就让计数器++
int size(TreeNode root){
int count=0;
if(root!=null){
count++;
count+=size(root.left);
count+=size(root.right);
}
return count;
}2.子问题思路
树中节点个数是左子树的个数+右子树个数+1(就是根节点)综合

int sizeSun(TreeNode root){
if(root==null){
return 0;
}
return sizeSun(root.left)+sizeSun(root.right)+1;
}2.叶子节点个数
int getLeafNodeCount(TreeNode root){
if(root==null){
return 0;
}
if(root.left==null&&root.right==null){
return 1;
}
return getLeafNodeCount(root.left)+getLeafNodeCount(root.right);
}
我刚开始没有考虑到递归的结束条件,就造成了空指针异常
应该加一条root==null
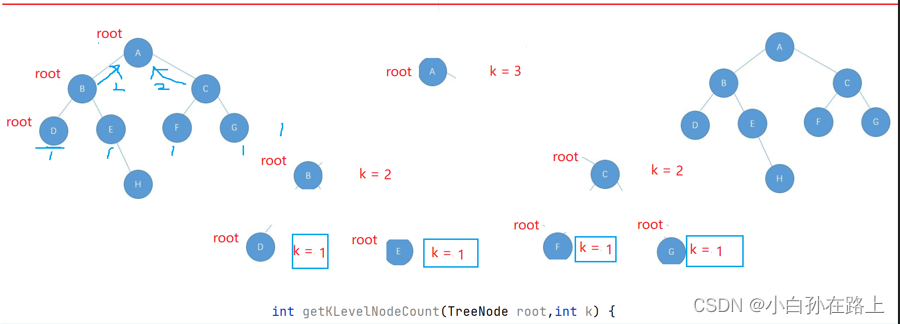
3.获取第K层节点的个数
这里的思路我觉得就是左子树层数和右子树层数节点总数,还是子问题思路
// 获取第K层节点的个数
int getKLevelNodeCount(TreeNode root,int k){
if(root==null||k<=0){
return 0;
}
if(k==1){
return 1;
}
return getKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);
}
4.获取二叉树的高度
思路
左子树高度和右子树高度的最大值.

这道题还是有一个注意点
就是在牛客计算中

如果这样算.会发现会超出时间限制

我们要注意不要重读计算

这道题的时间复杂度因为没有循环 就是递归的次数,有多少节点那就递归多少次也就是O(n)
空间复杂度.就要看左子树和右子树的最大高度选一个
因为这个题会不停的像一边开辟空间.那么空间复杂度也就是最大高度log2n.
5. 检测值为value的元素是否存在
这还是一样的思路/检验左子树和右子树是否有

这里跟之前的子问题遍历是一样的思路,
那就需要调用左边的然后接收这个左子树的节点值,来找,如果左边还没有
再调用右边的再右边找,如果右边还没有
就说明这棵树没有
// 检测值为value的元素是否存在
TreeNode find(TreeNode root, char val){
if(root==null) {
return null;
}
if(root.val==val){
return root;
}
TreeNode ret=find(root.left,val);
if(ret!=null){
return ret;
}
ret=find(root.right,val);
if(ret !=null){
return ret;
}
return null;
}
因为可能是空的 ,所以处理一下异常
6.判断一棵树是不是完全二叉树
就构建两个队列,这道题最好用非递归的思路去做
构建循环,r
遍历一个节点就放入队列中,
然后弹出判断是否为空
不为空就弹入左节点右节点
然后再按顺序弹出判断
如果是非完全二叉树,他放入的顺序不是按左右左右放的,所以会出现null.节点这种情况

boolean isCo(TreeNode root){
if(root == null) return true;
Queue<TreeNode> queue=new LinkedList<>();
queue.offer(root);
while(true){
TreeNode ret=queue.poll();
if(ret!=null){
queue.offer(ret.left);
queue.offer(ret.right);
}else{
break;
}
}
while(!queue.isEmpty()){
if(queue.peek()!=null){
return false;
}
queue.poll();
}
return true;
}