[NOIP2002 普及组] 过河卒

一、题目描述

棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 $(0,0)$、$B$ 点 $(n,m)$，同样马的位置坐标是需要给出的。

现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

二、输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

三、输出格式

一个整数，表示所有的路径条数。

四、样例输入

6 6 3 3

五、样例输出

6

六、提示

对于 $100\%$ 的数据，$1\le n,m\le 20$，$0\le$ 马的坐标 $\le 20$。

七、代码

#include <stdio.h>
long long f1[40][40];
long long f2[40][40];
int n, m, a, b;
void sign(int x, int y) {
	f2[x][y] = 1;
	f2[x - 1][y - 2] = 1;
	f2[x - 1][y + 2] = 1;
	f2[x - 2][y - 1] = 1;
	f2[x - 2][y + 1] = 1;
	f2[x + 1][y + 2] = 1;
	f2[x + 1][y - 2] = 1;
	f2[x + 2][y + 1] = 1;
	f2[x + 2][y - 1] = 1;
}

int main() {
	scanf_s("%d%d%d%d", &n, &m, &a, &b);
	//标记一下马的位置
	sign(a , b);
	f1[1][0] = 1;
	for (int i = 1; i <= n+1; i++)
	{
		for (int j = 1; j <= m+1; j++)
		{
			f1[i][j] = f1[i - 1][j] + f1[i][j - 1];
			if (f2[i - 1][j - 1]) //如果被标记过，则赋值为0
			{
				f1[i][j] = 0;
			}
		}
	}
	printf("%ld",f1[n + 1][m + 1]);
}

八、思路

• 首先我们将整个棋盘记作一个二维数组，注意二维数组的类型应当为长整型long long，否则可能会超出！

long long f1[40][40];
long long f2[40][40];

• 由题意我们可以知道，马所在的点和马所有跳跃一步可达的点都是卒不可以走的点
• 对此我们可以定义一个方法，利用已知的马走日的规律，将马所在的位置以及马可到达的位置，标记为1，方便后续操作
  

void sign(int x, int y) {
	f2[x][y] = 1;
	f2[x - 1][y - 2] = 1;
	f2[x - 1][y + 2] = 1;
	f2[x - 2][y - 1] = 1;
	f2[x - 2][y + 1] = 1;
	f2[x + 1][y + 2] = 1;
	f2[x + 1][y - 2] = 1;
	f2[x + 2][y + 1] = 1;
	f2[x + 2][y - 1] = 1;
}

• 准备工作做好了之后，就可以进入本题的核心部分啦，如何计算路径的条数呢？我们已经知道了要到达的B点的坐标，以及卒开始的位置（0，0），本题带有一点小学奥数题的味道了
• 就以下图为例，假设只能向下向右走，计算节点A到达节点B有多少条路径，很显然有两条路径

• 再以下图为例，假设只能向下向右走，计算节点1到达节点9有多少条路径，只需从节点2开始，依次计算并累加上一个节点到此节点的路径（图中红色数字就是到对应节点的路径条数；例如：节点1到5的路径条数=节点1到2的路径条数+节点1到3的路径条数）

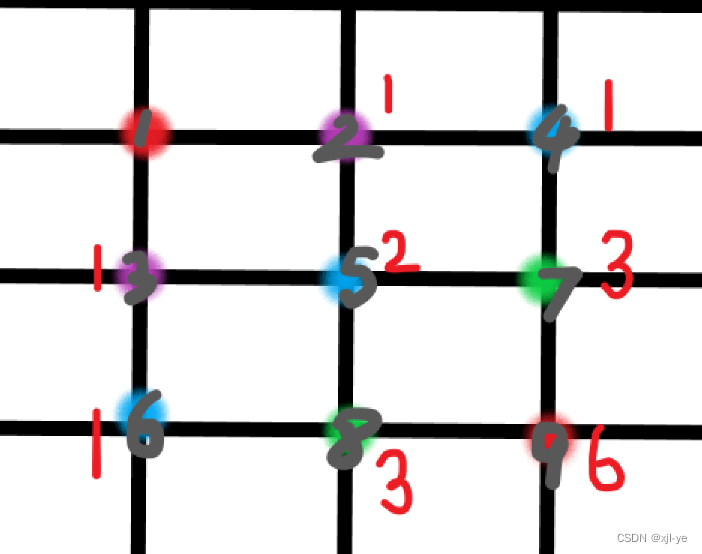
• 本题的思路与此思路相似，想知道到节点9的路径数，就需要知道到节点7和8的路径数，一步一步向前推，但注意：与此不同的是要去掉马所在的点和马所有跳跃一步可达的点，即将这些点标记出来，不去遍历这些点。

int main() {
	scanf_s("%d%d%d%d", &n, &m, &a, &b);
	//标记一下马的位置
	sign(a , b);
	f1[1][0] = 1;//表示初始的点,未被标记过
	for (int i = 1; i <= n+1; i++)//i从1开始，对应图的X坐标，X坐标最大为n+1
	{
		for (int j = 1; j <= m+1; j++)//j从1开始，对应图的Y坐标，Y坐标最大为m+1
		{
			f1[i][j] = f1[i - 1][j] + f1[i][j - 1];//当前遍历到的节点的路径数 = 此节点的左边节点路与上边节点的径数之和
			if (f2[i - 1][j - 1]) //如果被标记过，则赋值为0
			{
				f1[i][j] = 0;
			}
		}
	}
	printf("%ld",f1[n + 1][m + 1]);
}