1 三角函数合成

函数正交（数字信号处理-3-函数的正交），那它们相互之间无法通过组合得出对方的表达式，如：sinx 与 cosx 正交，acosnx 是无法表示 sinx 的。相互正交的各类三角函数是制作许多波形的基本单位。

1.1 同周期函数合成

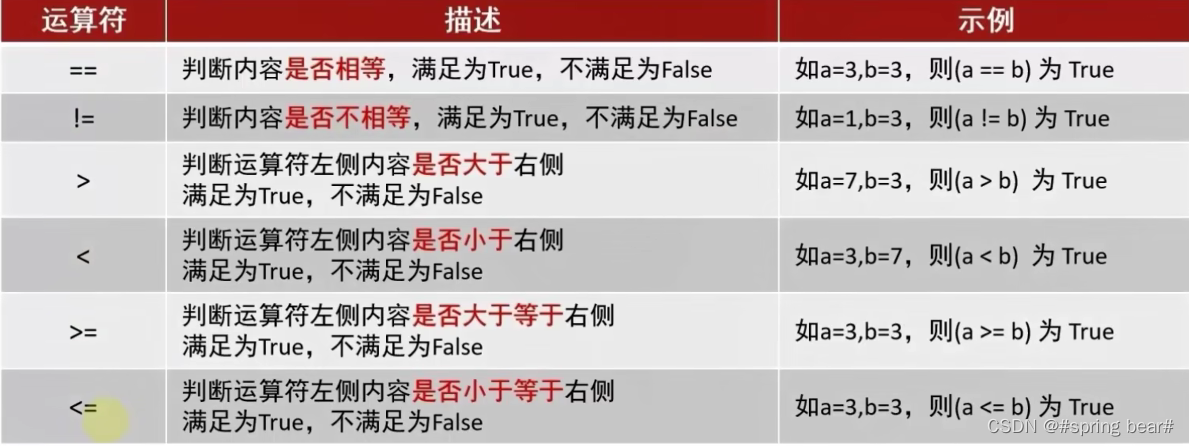
acosx 与 bsinx 同周期，不同振幅。将两个函数画在分别以 a 和 b 为半径的圆周上。cosx 与 sinx 两者相差 π/2（90度）（数字信号处理-2-三角函数与谱），两者呈正交关系，使用矢量的合成。合成向量表示为 acosx + bsinx 。

合成后的半径为 $r=\sqrt{a^2+b^2}$

2cosx+2sinx 的波形的振幅是 $r=\sqrt{2^2+2^2}=\sqrt{8}=2.828$

将 a 与 b 进行恰当的组合，虽然不能改变周期，但能自由组合成各种振幅和相位。sinnx 与 cosnx 合成时是 n 个周期，也即对应角频率 ω。这个 n 周期与 r 组合就能得到频谱图。

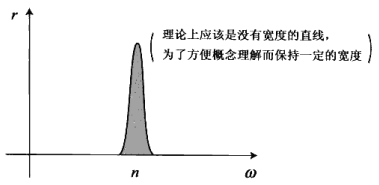
1.2 周期不同三角函数合成

同样，可以对不同周期三角函数合成
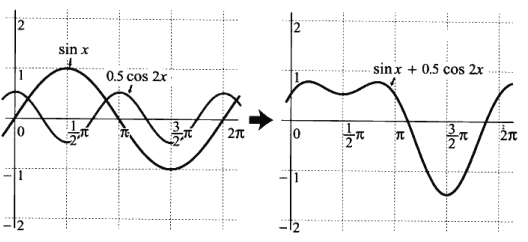
如 sinx + sin2x :

sinx+0.5cos2x :

2 傅里叶级数

如果将多个 sin 与 cos 函数进行合成，就能得到更加复杂的函数。

傅里叶级数用公式表示，如下：

常数项 1/2a₀ 能使三角函数合成的波形全体上下移动

在 Σ 中的第 n 项，这个 n 既决定了第 n 项振幅大小的数值，也是第 n 项三角函数的周期

傅里叶级数展开要求 F(x) 有某个周期特性，也就是以利用周期函数的合成为前提。对于非周期函数，取某个区间，以这个区间内的波形为周期波形而重复出现，形成周期函数，然后就能对波形进行展开了。

a₁、a₂、a₃…b₁、b₂、b₃叫做傅里叶系数，这些系数的值能决定 F(x)波形的形状。

看一个波形合成的例子， a_nsinnx，这里的 n 从1、2…到 40。a_n为 n 的倒数，a_n=1、1/2、1/3…。

3 时间函数与频率谱

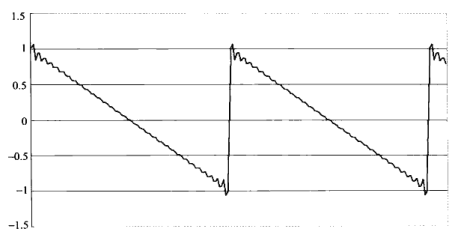
在半径为 3 的圆周上，以角速度(角频率) ω 旋转的点可以用 y =3sinωt = 3sinx 表示, x 表示为 ωt，其中 ω 固定，x 表示 t 的函数 。同理，在半径为 4 的圆周上，以 2ωt 旋转的点可以用 y = 4sin2x 表示。在半径为 2 的圆周上，以 3ωt 旋转的点可以用 y = 2sin3x 表示。将这些函数加起来，得到如下结果。

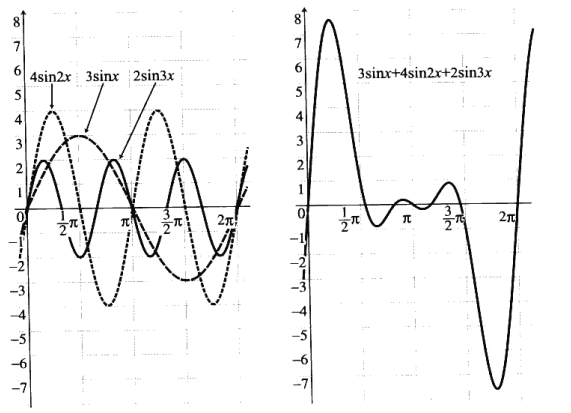
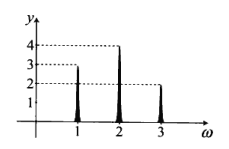
这种随时间变化的函数叫做时间函数。接下来，以 ω 为横轴，纵轴为各个角频率的振幅，将上图转换为频率谱的图像，这样就完成了从时间函数到频率谱转换的流程。

参考

漫画傅里叶解析
Python数字信号处理应用