• 参考视频 MIT 微积分课程

两个函数相乘的导数

• $(f(x)g(x){)}^{{}^{\prime }}=f^{{}^{\prime }}(x)g(x)+g^{{}^{\prime }}(x)f(x)$ 这是我们都非常熟悉的公式，熟悉到根本不知道是咋推出来的
• 其实推导这个公式有两种方法，一种就是靠定义 $f^{{}^{\prime }}(x)=\frac{f(x+\Delta x)-f(x)}{\Delta x}$，另一种推导的方式是一个很简单的作图法
• 对于第一种方法的证明，可以参考这篇文章
• 本文主要是通过第二种思路进行证明

几何法证明导数相乘

• $f(x)$

• $g(x)$

• $p(x)=f(x)g(x)$

• 首先我们简写一下方便表示，将 $p=f\cdot g$

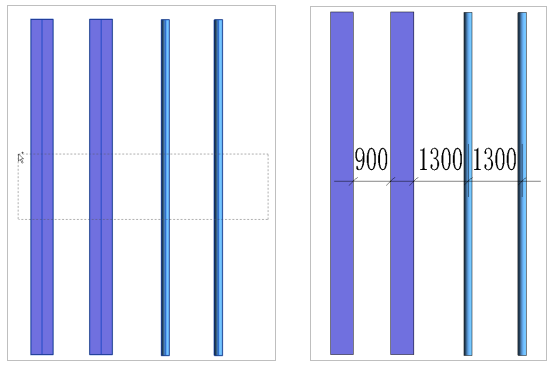
• 然后我们把这个面积画一下
  

• 现在 $x$ 发生了一点点改变，这个改变是 $\Delta x$

• 那么面积图相应的也就变了：
  

• 根据这个图：
  $$\Delta p=f\cdot \Delta g+g\cdot \Delta f+\Delta f\Delta g$$
  $$\frac{\Delta p}{\Delta x}=\frac{f\cdot \Delta g+g\cdot \Delta f+\Delta f\Delta g}{\Delta x}$$

• 当对 $\Delta x$ 取极限的时候 ${\lim }_{\Delta x\to 0}$ 公式就变成了

$$\frac{dp}{dx}=f\frac{dg}{dx}+g\frac{df}{dx}+\frac{\Delta f\Delta g}{\Delta x}$$

• 而很显然 $\frac{\Delta f\Delta g}{\Delta x}$ 是个二阶项，通俗来说也就是说他小的可以忽略，因为如果我们按照常规对他取极限你会发现 $$\underset{\Delta x\to 0}{\lim }\frac{\Delta f\Delta g}{\Delta x}=\frac{df}{dx}\cdot \Delta g$$
• 而由于 $\Delta x\to 0$ 所以 $\Delta g\to 0$ 所以这一项的结果就是 $0$，所以就只剩下前面两项。
• 所以，这个相乘项的导数证明完成

两个函数相除的导数

$$q(x)=\frac{f(x)}{g(x)}$$

• 现在对 $q(x)$ 求导公式进行推导，首先把除法转换成乘法公式：
  $$f(x)=q(x)g(x)$$
  $$f(x{)}^{{}^{\prime }}=\frac{df}{dx}=q\frac{dg}{dx}+g\frac{dq}{dx}$$

• 现在要组合出 $\frac{dq}{dx}$ 单独一项

$$\frac{df}{dx}-q\frac{dg}{dx}=g\frac{dq}{dx}$$

$$\frac{df}{dx}=\frac{f}{g}\cdot \frac{dg}{dx}+g\frac{dq}{dx}$$

• 两边同乘 $g$

$$g\frac{df}{dx}=f\frac{dg}{dx}+g^2\frac{dq}{dx}$$

• 而 $q=\frac{f}{g}$ 所以式子最终等于得证：

$$\frac{dq}{dx}=\frac{g\frac{df}{dx}-f\frac{dg}{dx}}{g^2}$$