目录
1. 理解刚体的“自由度”(Degrees of Freedom, DOF)
1.1 平面运动 (2D)
1.2 空间运动 (3D)
2. 统一描述:引入“体坐标系”(Body Frame)
3. 从“状态”到“运动”:引入微分
3.1 补充:如何理解微分
4. 移动状态 - 位置向量 (Position Vector)
4.1 关于向量的两种含义
5. 转动姿态 - 旋转矩阵 (Rotation Matrix)
5.1 旋转矩阵与投影 (Direct Cosines)
5.1.1 点积 “⋅” (内积) 得到投影
5.1.2 一句话概括 (旋转矩阵)
5.2 计算旋转矩阵实例
5.2.1 例1 (简单情况) :
5.2.2 例2 (需要投影计算) :
6. 随堂测试 (姿态->世界坐标)
- 台大公开课链接:機器人學一 (Robotics (1)) - 物體在空間運動之描述 (一) - 第 1 周 | Coursera
- 视频链接:1-1 导论_哔哩哔哩_bilibili
- 上回书说到:机器人学入门 (从机械手臂开始的智能世界) 笔记 0.1 (台大机器人学-林沛群)-CSDN博客
- 以下是视频课程的详细笔记(后续会持续更新)
本系列课程将深入探讨机械手臂的运动学与操作。在正式进入机械手臂的具体内容之前,我们需要补充一些必备的数学基础,核心在于如何精确地描述一个“刚体”(Rigid Body)的运动状态。这是因为在后续分析中,我们通常将机械手臂的各个部件视为刚体来处理。
补充:
- 刚体是一个理想化的固体,其大小和形状在受到力的作用时保持不变,用于牛顿力学中对真实物体进行建模
1. 理解刚体的“自由度”(Degrees of Freedom, DOF)
我们先从最简单的情况入手:如何描述一个刚体的运动?
1.1 平面运动 (2D)
想象一个在平面上运动的物体,例如PPT上展示的那个绿色椭圆 。我们可以在平面上定义一个“世界坐标系”(World Frame),通常用 {W} 或 {A} 表示,它有X和Y两个轴 。
要描述这个物体在平面上的运动,需要多少个参数呢?
- 移动 (Translation):物体可以在平面上沿X轴(水平)和Y轴(竖直)移动 。因此,需要两个参数来确定其位置。这对应两个移动自由度 (3 DOFs)。
- 转动 (Rotation):物体还可以在平面内绕着某个点旋转(顺时针或逆时针)。这需要一个参数来描述其朝向 。这对应一个转动自由度 (1 DOF)。
总结来说,描述一个平面刚体的运动状态,总共需要 3个自由度(2个移动 + 1个转动)。
1.2 空间运动 (3D)
现在考虑空间中的刚体。世界坐标系相应地增加一个Z轴,变为三维坐标系 {W} (或 {A}) 。
- 移动 (Translation):物体的质心可以在空间中沿X轴(左右)、Y轴(上下)和Z轴(前后)移动 。因此,需要三个参数来描述其位置。对应三个移动自由度 (3 DOFs)。
- 转动 (Rotation):物体可以分别绕着X轴、Y轴和Z轴进行旋转 。这需要三个参数来描述其姿态。对应三个转动自由度 (3 DOFs)。
因此,描述一个空间刚体的运动状态,总共需要 6个自由度(3个移动 + 3个转动)。
2. 统一描述:引入“体坐标系”(Body Frame)
既然刚体运动包含移动和转动两部分,有没有一种简洁的方法能将它们统一起来表达呢?
答案是在 刚体本身 上建立一个坐标系,我们称之为“体坐标系”(Body Frame),通常用 {B} 表示 。这个坐标系是固定在刚体上的,会随着刚体一起运动。通常,我们会将体坐标系的原点建立在刚体的一个固定点上,比如质心 (被视为质量的中心) 。如上图所示,在绿色刚体上画上了一个橘色的坐标系统 {B} 。
通过引入体坐标系 {B},我们可以这样描述刚体的状态 :
- 移动状态:通过追踪体坐标系 {B} 的原点 (质心) 相对于世界坐标系 {A} (或称为{W}) 的位置来确定。
- 转动状态(姿态):通过观察体坐标系 {B} 的三个坐标轴(
,
,
)相对于世界坐标系 {A} (或称为{W}) 的朝向或姿态来确定 。
这样,借助体坐标系的原点位置和三个轴的姿态,我们就能同时描述刚体的移动和转动状态了 。
3. 从“状态”到“运动”:引入微分
前面讨论的是某个瞬间的几何状态(位置和姿态)。而“运动”是状态随时间的变化。如何描述这种变化呢 ?
- 速度与加速度:记录下刚体质心(即体坐标系原点)在不同时间点的位置,形成一条运动轨迹(如PPT中的红色曲线)。对这条轨迹(位置向量)关于时间进行一次微分,得到质心的速度;进行二次微分,得到质心的加速度 。
- 角速度与角加速度:类似地,通过对描述姿态的参数(我们稍后会详细介绍,如旋转矩阵)进行一次和二次微分,可以得到刚体的角速度和角加速度 。
3.1 补充:如何理解微分
- 图中曲线 f(x) 在 x0 处有一条切线,微分 dy 就基于这条切线来近似表示函数的变化
- 当 x 产生微小变化 △x 时,切线上对应的变化量就是 dy,它是对函数实际变化 △y 的近似
- 这种用切线的线性变化(微分 dy)“以直代曲” 来描述微小变化,正是微分的本质
因此,只要能精确描述刚体在任意时刻的几何状态(6个自由度),通过微分运算,就能掌握其完整的运动状态(速度、加速度、角速度、角加速度)。
4. 移动状态 - 位置向量 (Position Vector)
我们来更具体地量化描述移动。如前所述,我们在刚体(绿色椭圆)上建立了体坐标系 {B}(橘色),并在旁边设置了世界坐标系 {A} 。要描述移动,关键是追踪体坐标系 {B} 原点(通常设在质心)的位置 。
在三维空间中,这个向量有三个分量:,
和 Pz。例如,上图中的例子 向量 P = [10,3,3]
,意味着体坐标系原点在世界坐标系 X轴 上的投影距离是10,Y轴上是3,Z轴上也是3 。只要我们知道在任何时刻这三个分量的值,就能精确掌握刚体重心在空间中的位置 。
4.1 关于向量的两种含义
- 表示空间中的一个点 (Position):如我们刚才使用的位置向量
,它定义了体坐标系原点(或质心)在世界坐标系中的绝对位置 。
- 表示一个方向和大小 (Vector/Displacement):向量也可以仅表示一个方向和大小,例如体坐标系 {B} 的三个主轴
各自指向一个方向 。描述这些方向是理解刚体转动的关键,我们将在下一部分详细讨论 。
5. 转动姿态 - 旋转矩阵 (Rotation Matrix)
接下来,我们深入探讨如何描述转动,也就是刚体的姿态。我们利用体坐标系 {B} 的三个主轴  来代表刚体在空间中的姿态 。这三个轴向量都是从世界坐标系 {A} 的角度观察和描述的 。
来代表刚体在空间中的姿态 。这三个轴向量都是从世界坐标系 {A} 的角度观察和描述的 。
我们可以将这三个单位向量(表示方向)作为列向量,排列起来形成一个3x3的矩阵。这个矩阵被称为旋转矩阵 (Rotation Matrix),记作  (表示{B}(体坐标系)相对于{A}(世界坐标系) 的旋转):
(表示{B}(体坐标系)相对于{A}(世界坐标系) 的旋转):

这里, 表示 {B} 的X轴单位向量在 {A} 坐标系下的三个分量,
表示 {B} 的X轴单位向量在 {A} 坐标系下的三个分量, 和
和  同理 。左上角的 'A' 明确了参考坐标系 。
同理 。左上角的 'A' 明确了参考坐标系 。
这个旋转矩阵  包含了 {B} 相对于 {A} 的完整姿态信息 。
包含了 {B} 相对于 {A} 的完整姿态信息 。
5.1 旋转矩阵与投影 (Direct Cosines)
如何确定  这三个列向量呢?可以通过投影的方式 。例如,
这三个列向量呢?可以通过投影的方式 。例如, 的三个分量分别是
的三个分量分别是  向量在 {A} 的
向量在 {A} 的  三个轴上的投影长度 。其中,“⋅” 代表向量点积。
三个轴上的投影长度 。其中,“⋅” 代表向量点积。

5.1.1 点积 “⋅” (内积) 得到投影
5.1.2 一句话概括 (旋转矩阵)
- 用 {B}(体坐标系) 在 {A}(世界坐标系) 上的 (点积) 投影,来实现 体坐标系 (体姿态) 到 世界坐标系 的转换

其他两列  也是如此计算 。将所有九个点积(投影)结果组合起来,就得到了完整的旋转矩阵 :
也是如此计算 。将所有九个点积(投影)结果组合起来,就得到了完整的旋转矩阵 :

这种用 (体姿态) 向量在 (世界) 坐标轴上投影长度(方向余弦)来表示姿态的方法,也称为 Direct Cosines (直接余弦)。
5.2 计算旋转矩阵实例
5.2.1 例1 (简单情况) :
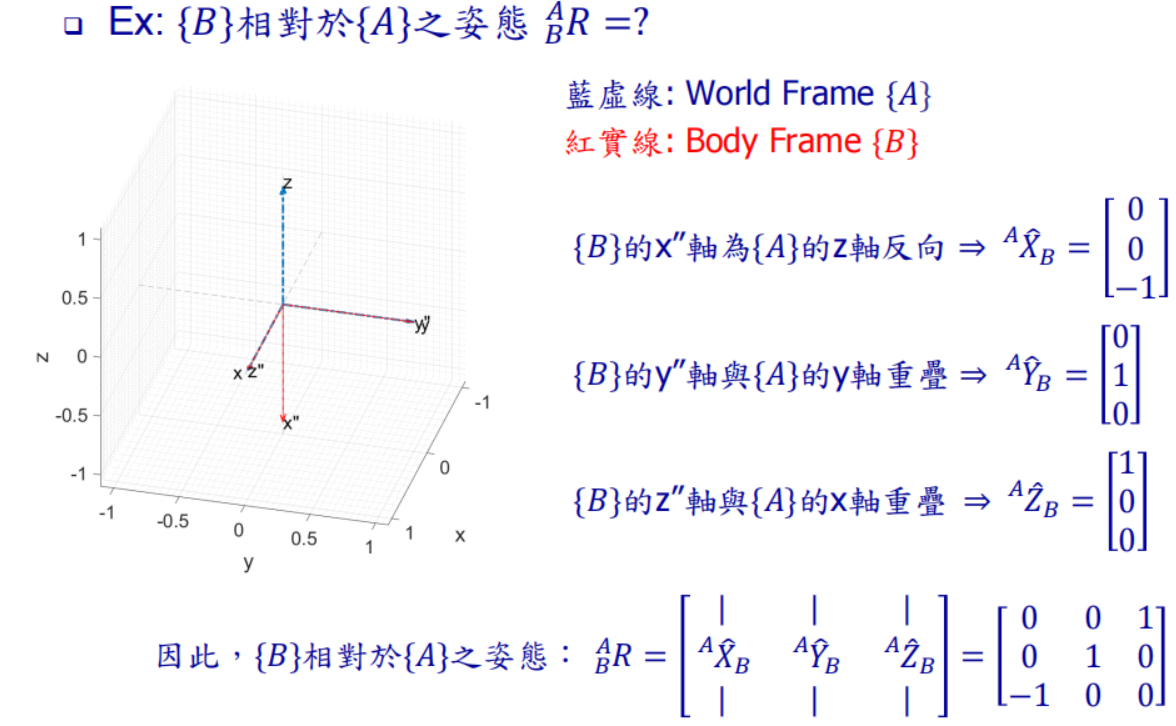

5.2.2 例2 (需要投影计算) :



6. 随堂测试 (姿态->世界坐标)

- 结合三视图,不难看出姿态的x''向量与世界坐标系的z轴重合,大小为-1,因此排除C和D
- 又因为姿态y''在y上的投影是负方向的,因此可以排除A
- 因此答案是B