摘要

        恒虚警率（CFAR）技术在雷达自动检测过程中起着关键作用。单元平均（CA）CFAR算法在几乎所有的多目标情况下都会受到掩蔽效应的影响。最小单元平均（SOCA）CFAR算法仅当干扰目标位于参考窗口的前后方时才具有较好的性能。有序统计（OS）CFAR算法在多目标情况下具有较好的鲁棒性，但计算复杂度较高。然而，当一个大目标连续占据多个单元时，无论是SOCA-CFAR还是OS-CFAR都无法避免掩蔽效应。为此，针对这些问题，提出了一种基于SOCA-CFAR的改进CFAR算法。仿真结果表明，改进的CFAR算法能够以较低的计算复杂度减轻掩蔽效应。所提出的CFAR算法的二维（2D）扩展也适用于距离多普勒矩阵（RDM），仿真结果证明了其性能优势。

        

引言

        雷达信号检测的目的是确定杂波或噪声背景中是否存在目标。先前的目标检测研究始于1943年至11世纪，经典的固定阈值检测基于具有定义统计特性和截面的噪声背景，其中有五种Swerling统计模型。最大的挑战是固定阈值无法适应由于温度变化或其他物理效应而变化的背景，导致较高的虚警率。杂波噪声包括接收机热噪声、地面物体、电子对抗等，被认为是高斯或非高斯的。在高斯模型中，高斯、瑞利和指数分布是最常见的概率密度函数（PDF）模型。在非高斯情况下，流行的PDF选择是对数正态分布和威布尔分布。因此，存在不同的检测器，例如线性、平方律或贝塞尔检测器，它们具有不同的检测性能和计算成本，其中，线性律和平方律检测器对于高斯噪声提供几乎相同的性能。为了在雷达自动检测系统中计算检测阈值，同时最小化杂波和噪声对虚警概率的影响，人们开发了恒虚警率（CFAR）算法。现有的CFAR检测程序通常使用滑动窗口来执行，通过滑动窗口估计假设模型的参数，并利用参考窗口中可用的数据来计算判决阈值。CFAR算法主要有两种：均值水平CFAR（ML-CFAR）和有序统计CFAR（OS-CFAR）。ML-CFAR基于两个邻域区域的算术平均值来估计背景噪声的功率，而OS-CFAR首先对数据序列按幅度排序，然后从有序序列中选择某个值作为估计值。

        ML-CFAR 可能是 CFAR 程序中最受欢迎的选择，它可以细分为单元平均 (CA) CFAR、最大单元平均 (GOCA) CFAR 和最小单元平均 (SOCA) CFAR。但是发现当参考窗口内存在一个或多个目标时，它的性能不佳。SOCA-CFAR 用于改善多目标情况下的性能。上述 CFAR 程序的局部噪声功率估计（用 Z 表示）可以分别描述为 Z = mean(x,y)、Z = min(mean(x), mean(y)) 和 Z= max(mean(x), mean(y))，其中 x 和 y 指的是两个邻域参考单元中的数据向量。 Rohling提出了一种基于顺序统计量的CFAR技术，在多个近距离目标的情况下，该技术优于SOCA-CFAR 。从参考窗口采集的样本首先进行排序，得到的序列称为有序统计量。可以通过以下公式实现：

其中下标表示排序序号，即索引K表示序列的第k个最小值，因此，x(1)和x(R)分别表示最小值和最大值，R是参考窗口的长度。与ML-CFAR方法不同，OS-CFAR选择一个确定的值x(K)作为局部噪声功率Z，因此，Z = x(k)，从而可以计算虚警概率Pfa，其表达式为:

其中 T 是缩放因子。OS-CFAR 程序在噪声边缘模型和双目标模型中表现出优于传统的 CA、GOCA 和 SOCA-CFAR 程序的性能。

        遗憾的是，几乎所有 ML-CFAR 程序在多目标和大目标情况下都会在一定程度上受到掩蔽效应的影响。尽管 OS-CFAR 在这两种情况下都表现良好，但它需要相当大量的序列排序和缩放因子计算。当目标足够大到跨越多个谱单元时，两者都会受到掩蔽效应的影响，导致决策不准确。为此，我们首先提出了一种改进的CFAR算法，该算法可以减轻多目标和大目标情况下的掩蔽效应。此外，我们还开发了一种基于二维滑动窗口技术的二维扩展CFAR算法，并将其应用于序列发射信号的连续波雷达系统的距离-多普勒矩阵（RDM）内的数据。本文的其余部分安排如下：第一节描述了信号模型、掩蔽效应和改进的CFAR算法。第二节给出了用于RDM的二维CFAR算法。第四节介绍了仿真结果，第五节得出结论。

改进的CFAR算法

        本节简要讨论了距离CFAR方案的数学信号模型，解释了掩蔽效应现象，并提出了一种改进的CFAR算法。

A. 距离CFAR方案的信号建模型

        CFAR算法通常应用于雷达探测系统。如图1所示，雷达系统发射啁啾信号，随后接收回波信号。回波信号经混频和下变频后，获得差拍信号，对其进行采样，然后通过快速傅里叶变换(FF'T)运算将其分解到不同的距离门中。图2以框图形式展示了信号处理和目标检测方案。首先对FFT运算后的样本进行幅度平方，然后根据不同的原理估计局部噪声功率，最终判断是否存在目标。在平方律检测器中，差拍信号的幅度平方记为Sm，其中m是目标距离下标，通常被认为是随机的。如图3所示，测试单元中的平方幅度序列记为D，其在测试单元两侧参考窗口内的对应序列分别记为xi和yi，其中i= 1,2,...,n。参考窗口的长度为R=2n。通过将局部噪声功率Z乘以缩放因子T，我们得到检测阈值S，其中S=T*Z，决策准则为：

其中，H0 为噪声环境下的假设，H1 为存在目标环境下的假设。假设背景噪声服从高斯白噪声，且服从独立同分布, 其包络服从瑞利分布。这样，序列 D 服从指数分布，其概率密度函数（PDF）为：

        其中，λ'是在假设H0下的平均噪声功率u，而在假设H1下 λ'=（1 + λ）其中是目标信号与噪声的平均功率比。

B 掩蔽效应

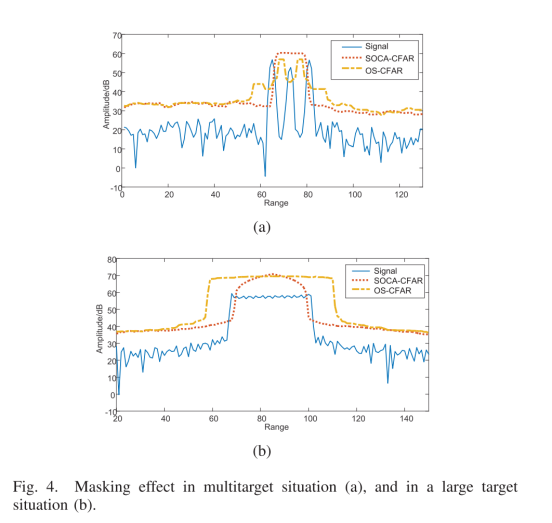
        在传统的ML CFAR算法中，目标被认为是独立的，并且它们之间的距离至少是参考窗口的一半，因此目标功率对局部平均噪声功率没有影响。但在实际应用中，这一假设很可能被违背。例如，当参考窗口内有两个或多个目标时，干扰目标的存在会增加估计的噪声功率以及阈值，从而产生掩蔽效应。图4(a)提供了一个示例，其中第二个目标被SOCA-CFAR算法掩蔽。

        与掩蔽效应类似，目标自掩蔽效应是指噪声功率估计值被目标自身的功率抬高的情况。当目标足够大，即其频谱跨越多个单元时，当其中一个谱单元被检测到时，其中一些目标会滑入参考窗口。如图 4(b) 所示，SOCA-CFAR 和 OS-CFAR 检测算法均会将大目标全部或部分掩盖。

C 改进的SOCA-CFAR算法

        CFAR检测的掩蔽效应实际上是由于参考窗口中存在目标引起的，这会增加局部噪声功率估计Z，从而增加虚警的可能性。

        为了减轻掩蔽效应，理想的检测算法应该在多目标和大目标情况下都具有鲁棒性。由于SOCA-CFAR检测算法采用的参考窗口从左向右滑动，因此可以提出一种改进方案来减轻参考窗口右半部分产生的目标掩蔽效应。如图5所示，关键在于进行加性反馈运算，当存在目标时，用噪声功率估计Z代替目标单元的值。

同时，在估计噪声功率时忽略与待测单元直接相邻的保卫单元。这样，参考窗口中的目标对噪声功率估计几乎没有影响。假设现在目标 A 位于第 k 个距离门，其局部噪声功率估计为 Zk，将目标功率 Dk 替换为 Zk，则测试单元的噪声功率估计 Dm（其中 m > k）可表示为：

        由于在同质噪声背景下，参考窗口中的样本是独立同分布的，因此改进的 SOCA-CFAR 具有与对话估计相同的估计 Z，如下所示：

因此，所提算法具有与SOCA-CFAR 相同的误报概率Pfa，Z和Pfa的PDF分别为：

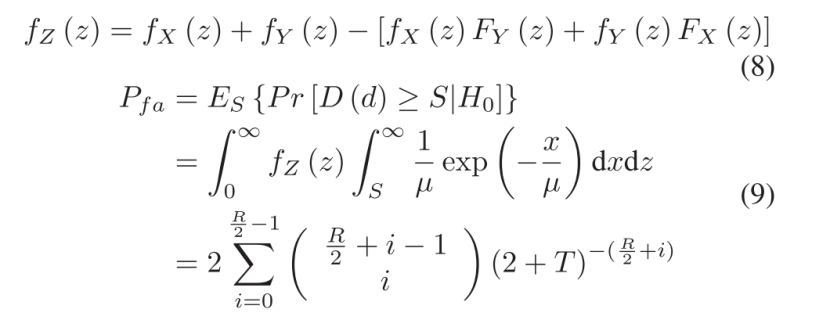
其中，fx(z)和fy(z)分别是X和Y的概率密度函数（PDF），Fx(z)和Fy(z)分别是相应的累积分布函数（CDF），μ是噪声功率。虚警概率Pfa与μ无关，因此改进的SOCA-CFAR算法具有恒定虚警率的特征。表1总结了该算法的具体步骤。

一种改进的二维CFAR算法

        上述CFAR方法适用于从一个chirp信号采样的一维数据。对于连续波雷达系统，它会发射一系列chirp信号，如图6所示。接收回波信号并将其与发射信号混合，然后进行下变频以获得周期性的差拍信号。每个差拍信号并行采样，并在此基础上进行FFT运算。得到的频谱按列存储在一个二维矩阵中，其差拍频率为fB=-2RB/T，其中B和T分别为chirp信号的带宽和持续时间，c表示光速，R表示目标与雷达系统之间的距离。在第二阶段，对上述矩阵的每一行进行FFT运算，测量当fD=-2v/λ时的多普勒频率，其中v表示径向速度，λ表示chirp信号的波长。这样，2DFFT 运算将差拍信号分解到不同的距离和多普勒门中，从而构建距离-多普勒矩阵 (RDM)，如图 6 所示。

        为了提高处理效率，本文进一步提出了一种 2D CFAR 算法。对于 RDM，参考窗口可以是矩形或十字形，本文选择十字形窗口进行演示，如图 7 所示。参数 M 和 N 分别为参考窗口在距离和多普勒方向上的长度。保护单元也相应地设置。对于本文提出的 2D CA-CFAR 算法，局部噪声功率 Z 是根据十字形参考窗口内观测值的算术平均值来估计的，其公式如下：

        其中, xi和yi分别是沿距离和多普勒方向样本幅值的平方。文献指出，CA-CFAR算法对掩蔽效应敏感，这一缺陷会传递到二维参考窗方法中。与二维CA-CFAR算法相比，二维SOCA-CFAR算法通过估计局部噪声功率Z：

        式中,Z1和Z2是基于SOCA原理的距离和多普勒参考窗噪声估计,实现了一定的性能提升。同理，二维OS-CFAR检测算法可以通过执行局部噪声功率估计来实现，式中：

        其中 x(k1) 和 y(k2) 分别是两个参考窗口内的噪声功率估计。根据上一节的分析，本文方法与SOCA-CFAR方法的区别在于增加了一个加法反馈操作，用局部噪声功率估计代替目标功率。同样，改进的二维SOCA-CFAR算法如图7所示。为了进一步减少计算负担，检测谱峰并将其存储在向量Dp = [Dp1,Dp2,..,DpL,]中，其中L是谱峰的数量。然后对每个谱峰进行CFAR检测。表2总结了二维改进SOCACFAR算法的所有步骤。

仿真

        为了说明基于平方律检测器及其二维扩展的SOCA-CFAR算法的性能优势，在Matlab编程环境中对雷达检测系统进行了仿真。在多目标情况下，考虑三个目标，它们与雷达系统的距离分别为40、45和50 m。所有目标均受高斯分布背景噪声污染，信噪比分别为15.56、12.04和15.56 dB。在大型目标情况下，其径向范围为4l至6l m，信噪比为10 dB。在两种情况下，虚警概率Pfa均设置为1e-6。

        图8示出了三种CFAR算法在多目标情况下的检测性能。改进的SOCA-CFAR算法消除了掩蔽效应，正确检测出了三个目标，而传统的SOCA-CFAR和OS-CFAR算法对掩蔽效应比较敏感，虽然可以通过增加窗口长度R来改善这一不足。例如，在图8(a)中，第二个目标在R=16时被掩蔽，而在R=32时OS-CFAR可以检测到，而SOCA-CFAR仍然将其掩蔽。通过比较图8(a)和图8(b)，我们观察到当K=R/2时OSCFAR的检测精度高于K=3R/4时。

        图9展示了当考虑跨越多个谱单元的大型目标时，所有考虑的CFAR算法的仿真结果。所提出的改进SOCA-CFAR算法也能正确检测出大目标，而另外两个算法在一定程度上受到了掩蔽效应的影响。

        为了验证增强型CFAR算法的鲁棒性，进一步考察了三种CFAR算法在不同信噪比（SNR）下的检测概率Pd。初始虚警概率Pfa和参考窗口长度R分别设为Pfa=1e-6和R= 32，仿真结果通过对500次独立试验取平均值获得。在多目标情况下，三个目标距离雷达系统分别为40、45、50 m；在大型目标情况下，其径向范围为42.24至48.06 m。如图10和图11所示，可以看出改进的SOCA-CFAR算法优于传统的SOCA-CFAR算法和OS-CFAR算法。同时需要注意的是，OS-CFAR算法的性能略逊于提出的算法，且计算复杂度更高。

 

        此外，还对四种CFAR算法的二维扩展在不同信噪比下的性能进行了仿真研究。距离和多普勒方向上的参考窗口长度分别设置为M=32和N=16，在二维OS-CFAR算法中，参数K1和K2分别为3M/4和3N/4。采用两个观测值作为守卫单元，虚警概率Pfa为1e-6。目标随机生成，距离为50至60米，速度为-5至15米/秒，其中负号表示朝向雷达系统。

        图12给出了2D CFAR算法在不同情况下的检测概率Pa，其中目标数量分别为1、3、5、7、9和11。当只有一个目标时，所有2D CFAR算法都具有可接受的性能。当目标数量增加时，2DCA-CFAR的性能严重下降，在所有考虑的信噪比情况下，当目标数量为1l个时，它几乎丧失了检测能力。此外，2D OS-CFAR算法的性能与2D SOCA-CFAR算法相当。同样显而易见的是，改进的2D CFAR在四种2D CFAR算法中具有最佳性能。

结论

        针对雷达检测系统，提出了一种改进的SOCA-CFAR算法。该算法的关键在于通过降低目标功率对平均噪声估计功率的敏感性，来缓解多目标和大目标对检测算法造成的掩蔽效应。提出的CFAR算法具有恒定的虚警概率。蒙特卡洛仿真表明，与传统的CA-CFAR、SOCA-CFAR和OS-CFAR算法相比，改进的SOCACFAR算法获得了更高的检测概率，并且这一优良特性在二维检测系统中同样有效。