DeepSeek从2025年1月起开始火爆,成为全球最炙手可热的大模型,各大媒体争相报道。我们可以和文心一言一样去官网进行DeepSeek的使用,那如果有读者希望将大模型部署在本地应该怎么做呢?本篇文章将会教你如何在本地傻瓜式的部署我们的deepseek,即便你是文科生也可以做到,不会涉及代码编程,只需要一些命令。
我笔记本:2019款拯救者,windows 10;内存8G,CPU:intel 9th i5;GPU:NVIDIA 1650 4G,256G固态+1T机械硬盘。其实只要你电脑系统是在windows 10及以上,且具有8G内存和30GB可用空间就基本可以部署最小版本的DeepSeek R1大模型和LLama3.2大模型。
相关的资源可以从我的百度网盘下载,当然也可以从各官网去下载,只不过会慢一些。
链接: https://pan.baidu.com/s/15H48zFG394P23b7wM2nTXA
提取码: iipt
本地部署DeepSeek和llama
本节将详细介绍如果通过Ollama和Open WebUI在本地计算机环境中部署DeepSeek R1和LLama 3.2大模型。
1.安装Ollama
Ollama是一个开源的本地化大模型部署工具,旨在简化大型语言模型(LLM)的安装、运行和管理。它支持多种模型架构,并提供与OpenAI兼容的API接口,适合开发者和企业快速搭建私有化AI服务。
Ollama官方网址:https://ollama.com/
点进去以后界面如下,然后点击Download。
我们这里选择Windows版本,所以选择Windows,然后点击Download for Windows,这里有时候会让你登录注册后才可以下载,有些同学从这里下载会很慢,因此还是推荐从我的百度网盘下载。
下载完成以后,双击安装包文件“OllamaSetup.exe”完成安装。
注意:这里默认安装为C盘。
1.1更改大模型下载位置
这一步并不是必须的,如果你C盘位置足够可以不用管。如果你希望更改其他位置可以看这一部分。
安装完毕后,如何检验Ollama是否安装完毕呢?方法很简单,按键盘上的windows键+R键,然后输入cmd并确定,如下:
紧接着在跳出的窗口输入以下命令: ollama --version 当我们可以看到打印的ollama版本就说明安装成功了。
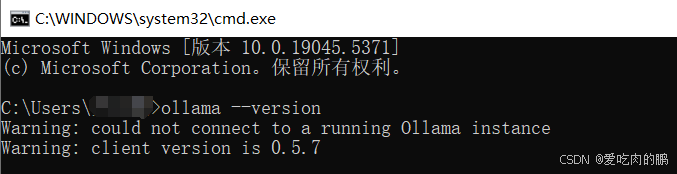
后续下载的各类大模型也均存储在C盘,因此如果你希望把大模型放在其他盘,例如我这里是F盘,操作如下:
我是在F盘新建了一个ollama的文件夹。如下:
![]()
下载的各类大模型一般默认位置为:C:/User/你的用户名/.ollama/models/
然后将上述models整个文件夹剪切到你自己新建的文件中,我这里是F:/ollama/models,如下:
![]()
到了这还没有完,我们还需要修改环境变量,便于让后续的Ollama自动找到我们的大模型。
右键“此电脑” :
:
然后点击属性,点击高级系统设置。
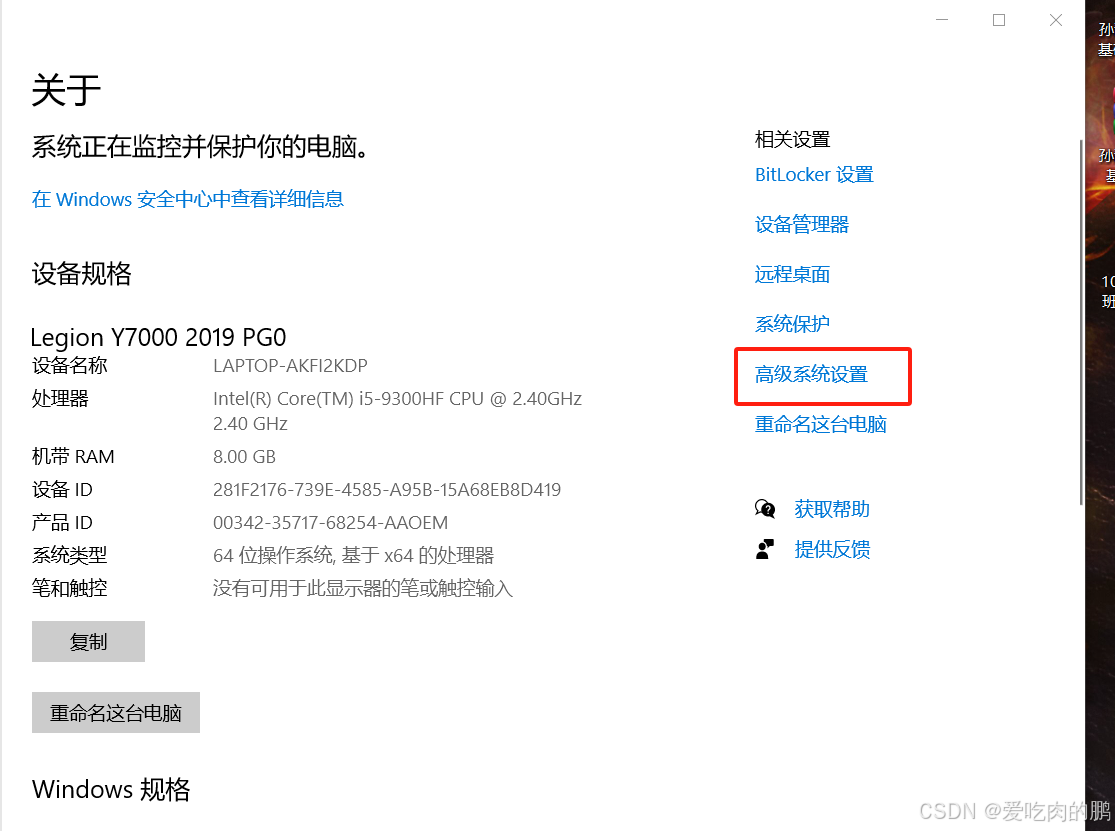
在系统属性窗口,点击高级-->环境变量。
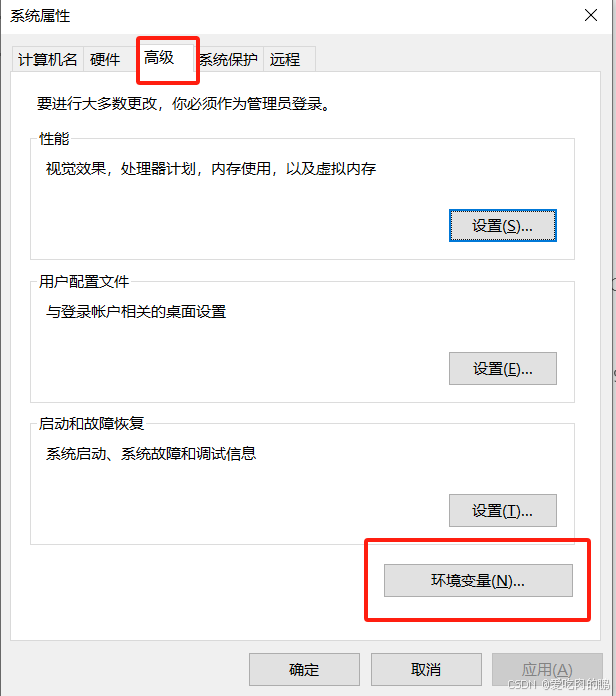
在跳出来的环境变量窗口用户变量中点击新建。
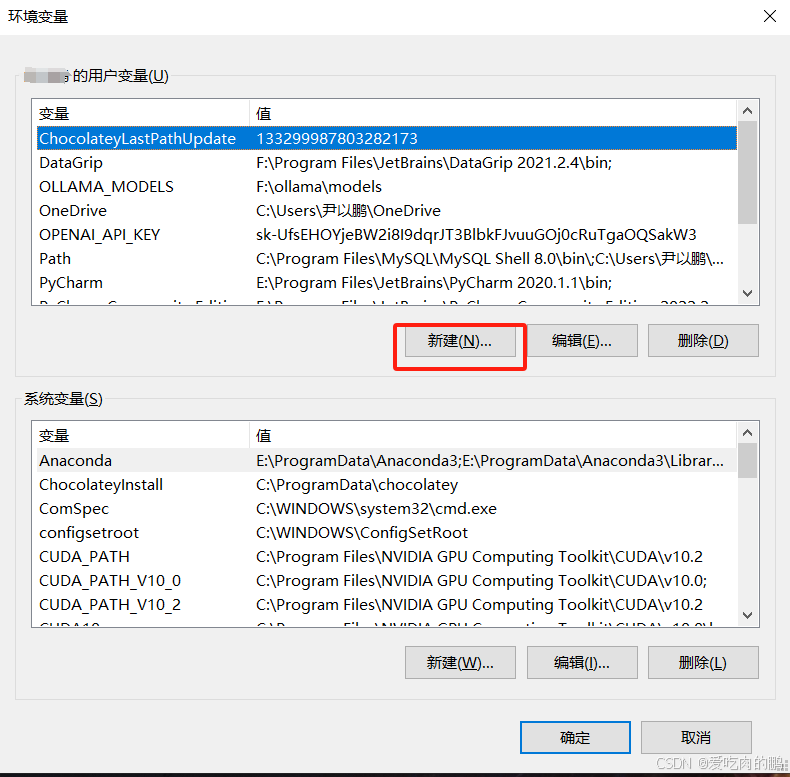
输入以下内容:
变量值为你存储大模型的位置,根据自己的实际位置进行修改。
2.下载DeepSeek R1大模型
我这里仅以DeepSeek R1大模型为例,其他大模型例如LLama也是一样的操作。
模型下载地址:https://ollama.com/library/,该地址进去后有各类大模型。
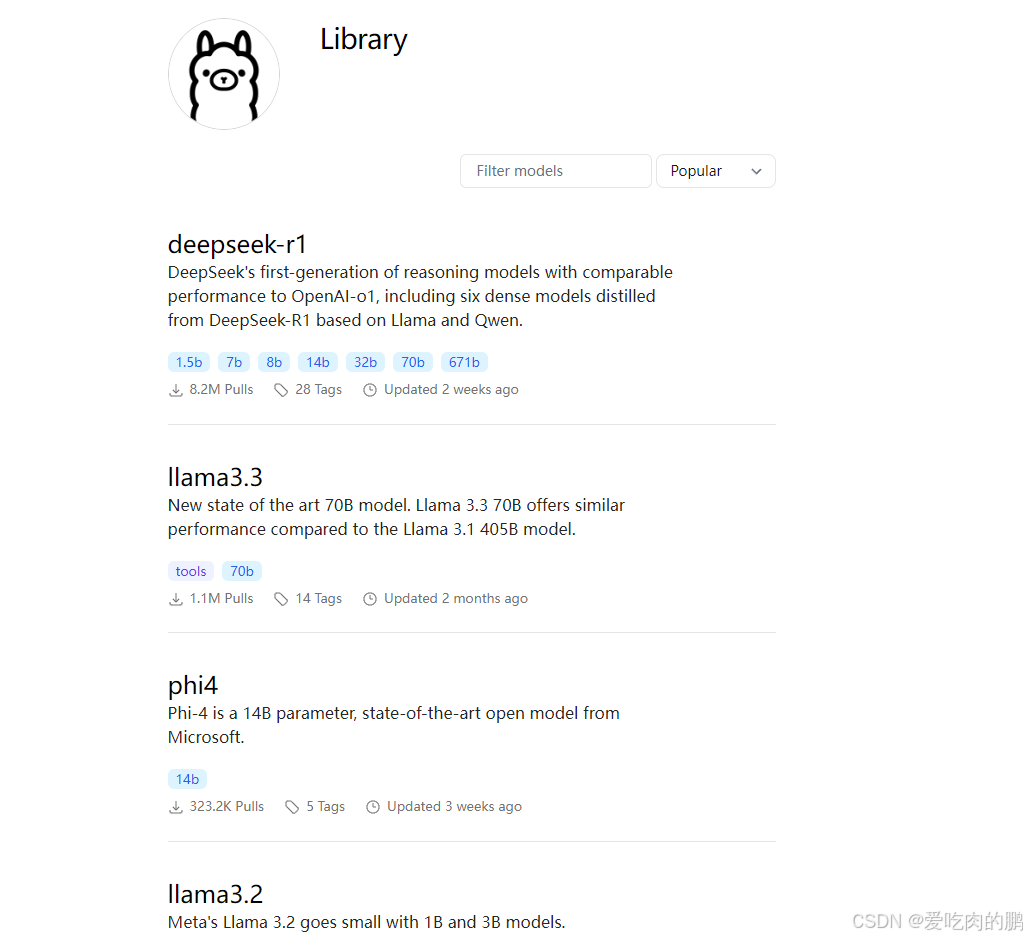
但这里给一个更方便的下载方法,让Ollama为我们自己下载。
因为我这里的显存比较小,因此我选择下载的是deepseel-R1,llama3.2也可以带起来。
只需要在cmd中输入ollama run deepseek-r1:1.5b命令即可下载或运行。(如果之前没有下载会自动下载,如果已经下载过了,输入该命令后会自动运行大模型),这里的下载速度取决你的网速的和模型大小。
安装成果后你就可以和deepseek对话了,如下,关闭窗口就退出模型了:
如果你要查看你下载了哪些大模型,命令如下:
ollama list

3.安装Open-WebUI
上述的方法使用大模型是不是感觉太Low了,不像GPT或者文心一言有一个网页的交互界面,因此也有前人为我们造好了轮子,我们直接拿来用就行,这个框架框架就是Open-WebUI。
但是安装此框架之前需要你电脑上安装好python3.12,注意要3.12版本!太低不兼容,也不建太新的,咱们就按官方推荐的来。
然后在cmd中输入以下命令:
pip install open-webui -i https://pypi.tuna.tsinghua.edu.cn/simple
注意:这里的安装的时间可能会比较长,如果长时间不动或者卡住,可尝试按一下回车键。
安装完成后,同样在cmd中输入open-webui serve命令开启我们的UI界面,看到下面界面并不意味着已经完全启动成功,咱们还需要继续等待。
直到出现以下类似的信息后,才说明启动成功。

接下来就是见证奇迹的时刻!!!打开你的浏览器,输入网址:
http:/localhost:8080
注意:第一次登录的时候,需要你自己先注册到本地一个管理员账户。
如果你想切换大模型,可以点击下面的选项。
接下来你就可以实现对话啦~~~

注意:默认大模型是离线的,也就是不接入互联网。如果你希望联网,那么你可以进行如下设置:
点击左下角的账户,然后点击设置,找到如下设置,也可以用其他的搜索引擎,但需要API。
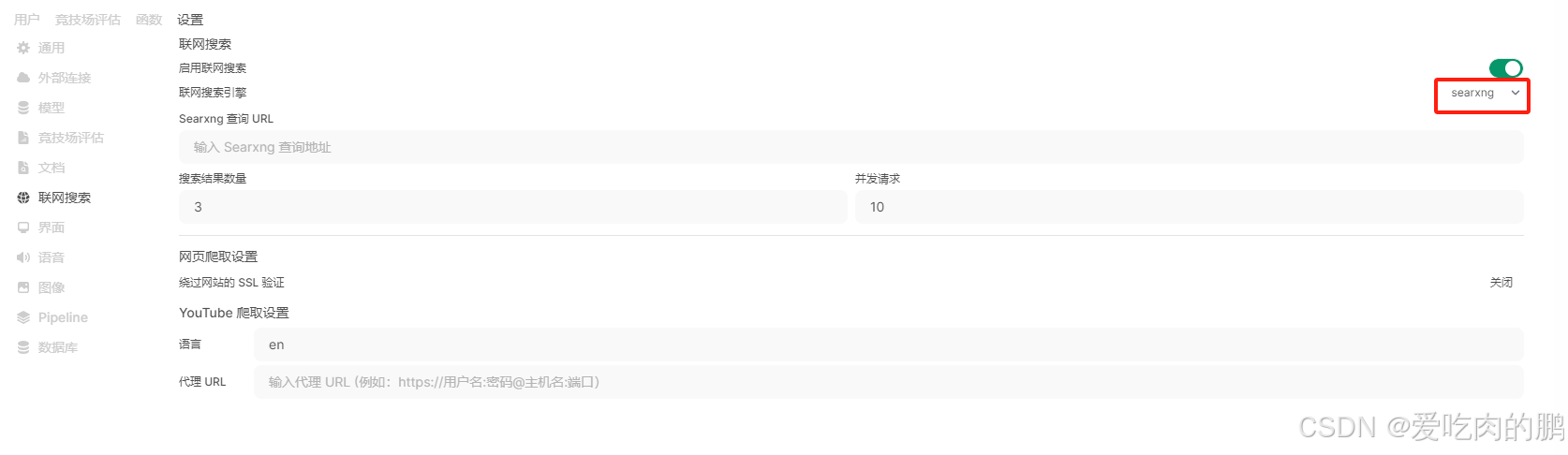
但是尝试了一下deepseek r1,感觉效果很一般,更大参数的模型效果会好一些。