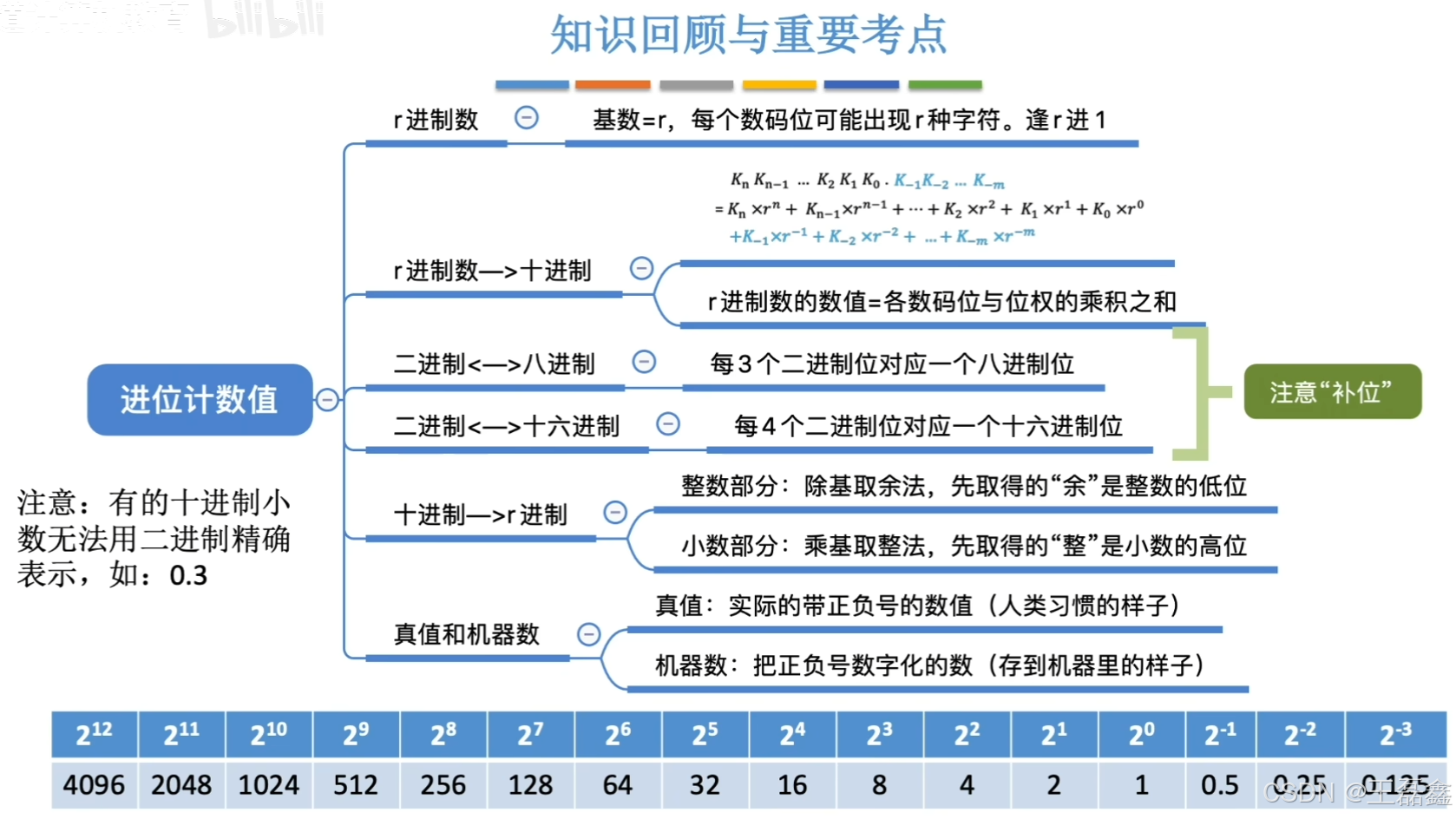
数据的表示和运算
提问:1.数据如何在计算机中表示?
2.运算器如何实现数据的算术、逻辑运算?

十进制计数法
古印度人发明了阿拉伯数字:0,1,2,3,4,5,6,7,8,9(符号反映权重)
十进制:975=9x100+7x10+5x1 (符号所在的位置也反映权重)
进位计数制:有0~9,共十种符号。逢十进一

以此类推,十进制的这种计数方式,我们会用每一个数码位乘以这个数码位所对应的一个实际的权值。这些权值都是十的某次方,因此我们才把它叫做十进制。
其实呢,十进制能推广到 r 进制。r 进制里,基数就是 r,每个数码位能用 r 种符号。像古巴比伦人用的 60 进制,每个数码位就有 60 种符号,现在咱们算时间,1 小时 60 分钟,就是 60 进制的应用呢。不过在计算机世界里,常用的是二进制、八进制和十六进制。
r进制计数法

1. 二进制:计算机中最常用基数为2的计数制即二进制。它仅有0和1两种数码,计数规则是“逢二进一”,任意数位的权为
,i是所在位数。
2. 八进制:基数是8,有0 - 7共8个不同数码,计数“逢八进一”。由于r = 8=
,所以把二进制中的3位数码编为一组就是1位八进制数码,二者转换很方便。
3. 十六进制:基数为16,有0 - 9、A - F共16个不同数码,其中A - F分别表示10 - 15,计数“逢十六进一”。因为r = 16 =
,所以4位二进制数码与1位十六进制数码相对应。可以用后缀字母标识数的进制,用B表示二进制数,用D表示十进制数(通常直接省略),用H表示十六进制数,有时也用前缀0x表示十六进制数。
在计算机中,有二进制、八进制、十进制、十六进制
计算机喜欢二进制,一是因为能用两个稳定状态的物理器件表示 0 和 1,像高电平低电平、电容电荷正负。二是 0 和 1 对应逻辑的假和真,方便做逻辑算。三是能用逻辑门电路做算术运算。不过二进制给人看不太方便,所以也常用八进制和十六进制。

二进制数转换为八进制数和十六进制数
对于一个二进制小数(既包含整数部分,又包含小数部分),在转换时应以小数点为界。其整数部分,从小数点开始往左数,将一串二进制数分为3位(八进制)一组或4位(十六进制)一组,在数的最左边可根据需要加“0”补齐;对于小数部分,从小数点开始往右数,也将一串二进制数分为3位一组或4位一组,在数的最右边也可根据需要加“0”补齐。最终使总的位数为3或4的整数倍,然后分别用对应的八进制数或十六进制数取代。
如果我们想要将二进制转换为八进制,那么只需要三个二进制为一组,然后将每组转换为对应的八进制符号即可。
各进制的常见书写方式
| 进制 | 书写方式 1 | 书写方式 2 | 书写方式 3 |
|---|---|---|---|
| 二进制 | 1010001010010B | - | |
| 八进制 | - | - | |
| 十六进制 | 1652H | 0x1652 | |
| 十进制 | 1652D | - |
十进制转换成任意进制数
一个十进制数转换为任意进制数,通常采用基数乘除法(注意,基数的值与进制相关)。这种转换方法对十进制数的整数部分和小数部分将分别进行处理,对整数部分采用除基取余法,对小数部分采用乘基取整法,最后将整数部分与小数部分的转换结果拼接起来。
除基取余法(用于整数部分):对整数部分进行除基取余操作,最先获取的余数是数的最低位,最后获取的余数是数的最高位(即“除基取余,先余为低,后余为高” ),当商为0时操作结束。
乘积取整法(小数部分):小数部分乘基取整,最先取得的整数为数的最高位,最后取得的整数为数的最低位(乘基取整,先整为高,后整为低),乘积为1.0(或满足精度要求)时结束。

注意:
- 十进制数转换为任意进制数时,对于除基取余法和乘基取整法,以及所取之数放置位置的原理,应结合 r 进制数的数值表示公式思考,避免死记硬背。
- 在计算机中,整数和小数有区别,整数可连续表示,小数是离散的,不是每个十进制小数都能用二进制小数精确表示(如 0.3 乘二取整无法得到精确结果),但任意二进制小数都可用十进制小数精确表示,需引起重视。
真值和机器数
真值:符合人类习惯的数字
机器数:数字实际存到机器里的形式,正负号需要被“数字化”。
| 类型 | 定义 | 正数示例(以 + 15 为例) | 负数示例(以 - 8 为例) |
|---|---|---|---|
| 原码 | 最高位为符号位,0 表示正数,1 表示负数,其余位为数值位的二进制表示 | 01111(假设用 5 位二进制表示,下同) | 11000 |
| 反码 | 正数的反码与原码相同;负数的反码是在原码的基础上,符号位不变,其余各位取反 | 01111 | 10111 |
| 补码 | 正数的补码与原码相同;负数的补码是在反码的基础上 + 1 | 01111 | 11000 |
| 移码 | 在补码的基础上,将符号位取反(一般用于浮点数的阶码表示) | 11111 | 01000 |