树的模拟实现

news2025/1/12 11:19:56

一.链式前向星

所谓链式前向星，就是用链表的方式实现树。其中的链表是用数组模拟实现的链表。

首先我们需要创建一个足够大的数组h，作为所有结点的哨兵位。创建两个足够大的数组e和ne，一个作为数据域，一个作为指针域。创建一个变量id，标记新来结点存储的位置。

接下来是模拟实现，当x有一个孩子y的时候，就把y头插到x的链表中。

首先id++，e[id] = y,为y结点开辟一块位置存储；接着我们用 ne[id] = h[x] 通过指针的思想，在y的指针域内存储上x的信息，最后将h[x] = id，将y的信息给x，为其他元素提供指针域信息。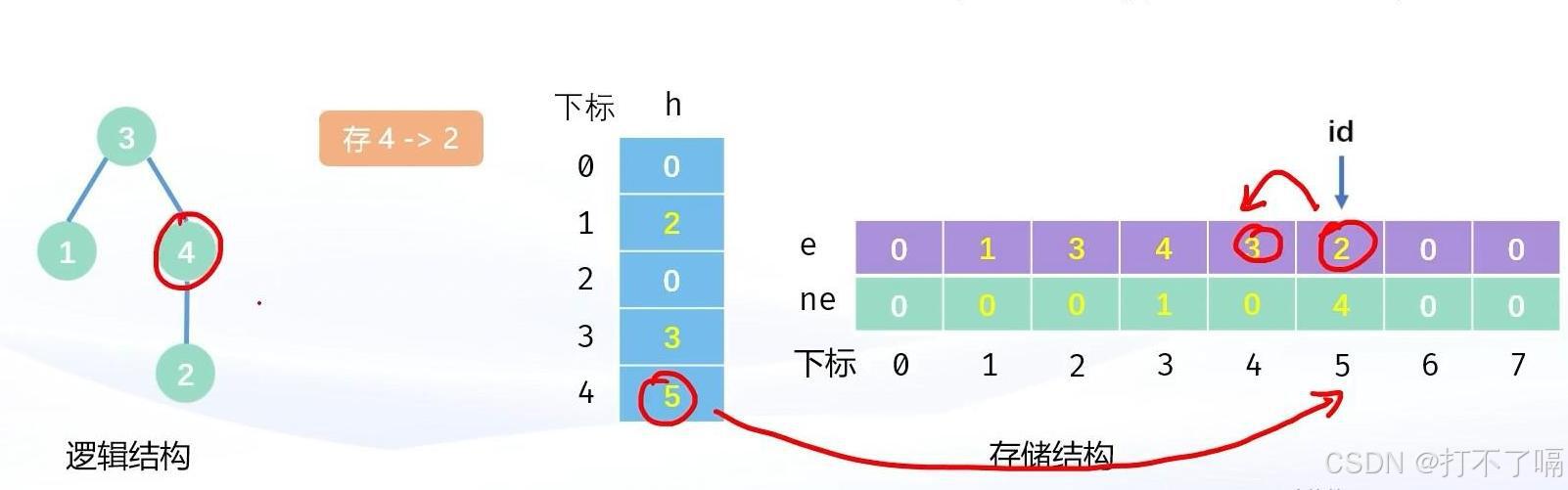

例如我们要在4上存2，先id++将2存储到数组中，令e[id] = 2，接着我们将ne[id] = h[4]，（先前的下标4中存储的是4），最后h[4] = id 存储指针域信息。那么这就相当于下标4中的h指向id = 5，e[5] 中存储的是结点2，2结点的指针域指向id = 4的下标，id = 4的下标中e[4] ，存储的是结点3。所以4结点就与2结点和3结点相连接。树就被模拟实现出来了。

下面是代码实现：

#include <iostream>
using namespace std;

int n;
const int N = 10;
int e[2 * N], ne[2 * N], h[N];//因为每个点都包含自己和其他，所以需要开辟结点大约2倍的空间
int id;

void add(int x, int y)
{
	id++;
	e[id] = y;
	ne[id] = h[x];
	h[x] = id;
}

int main()
{
	cin >> n;
	for (int i = 1; i < n; i++)//n个元素n-1条边
	{
		int a, b; cin >> a >> b;
		add(a, b); add(b, a);//将每一个结点都单独分开计算，所以需要调用两次函数
	}
	return 0;
}

二.顺序表实现树

我们的思想是，为每一个结点开辟一个数组，用map的思想，将数据的实际值与其下标进行对应减少复杂度，在对应的数组下标下存储其结点的值。

需要注意的是，此方法适合在算法竞赛中使用，使用的都是静态数组，需要人为的进行判断数组实际需要的大小。

接下来是代码实现：

#include <iostream>
#include <vector>
using namespace std;

const int N = 1e5 + 10;
int n;
vector<int> edges[N]; // 存储树

int main()
{
	cin >> n;
	for (int i = 1; i < n; i++)
	{
		int a, b; cin >> a >> b;
		// a 和 b 之间有⼀条边
		edges[a].push_back(b);
		edges[b].push_back(a);
	}
	return 0;
}