day12

今天是第12天，昨天主要是针对信号处理算法，可以提取出设备时序数据的时频特征为主，今日主要针对之前提到的8种算法中的时序分解、时序分割、时序再表征进行阐述

时序分解

工业上大多数设备通常都是呈现多尺度的效应，不同时间颗粒度上的规律和驱动因素各不相同，有些变化只在部分尺度上有所体现，比如常见的电力负荷预测，多半会将其分解为：趋势项（宏观经济和市场相关）、周期项（日历周期相关）、残余项（可以用天气、自回归项去拟合）。常见的时序分解的算法又：STL、奇异谱分析（SSA）、经验模态分解（EMD）、小波分析分解、SuperSmooth、传统的线性滤波等

STL（季节性趋势分解法）

核心功能：STL方法通过分解时间序列为 趋势（Trend）、季节性（Seasonal） 和 残差（Remainder），帮助我们理解数据的长期变化趋势、周期性波动以及随机噪声部分。这个方法特别适合季节性变化明显的时间序列。

算法流程：

1. 平滑趋势成分：使用局部加权回归（Loess）方法平滑时间序列，得到数据的 长期趋势。
2. 提取季节性：将趋势成分从原始数据中去除，然后通过计算季节性成分的平均值来提取 周期性的季节性波动。
3. 计算残差：将趋势和季节性成分从原始数据中减去，剩下的部分是 残差，通常是一些随机噪声或其他未捕捉到的模式。

举例：假设你在分析一年中每日的温度数据。STL可以帮助你分解出：

• 一年内温度的 长期上升或下降趋势（如全球变暖趋势），
• 每年季节性波动的 周期性波动（例如，夏季高温、冬季低温），
• 余下的 异常波动和噪声（如某些天气突变）。

奇异谱分析（SSA）

核心功能：奇异谱分析（SSA）通过将时间序列转换为矩阵，利用矩阵的 奇异值分解（SVD） 技术，提取出时间序列中的趋势和周期成分。SSA适合从复杂的信号中提取出周期性成分，广泛应用于信号处理、降噪等领域。

算法流程：

1. 构造轨迹矩阵：将时间序列切分为多个重叠的小窗口，每个窗口包含一段时间的数据。将这些窗口按列组成一个矩阵。
   • 比如，你有一个长度为10的时间序列，你选择一个长度为5的窗口，构造一个包含5列的矩阵。
2. 奇异值分解（SVD）：对矩阵进行奇异值分解（SVD），得到奇异值和奇异向量。
   • 奇异值代表了不同时间成分的重要性，奇异向量代表了这些成分的模式。
3. 重构信号：选择主要的奇异值和对应的奇异向量，重构出信号的 趋势 和 周期性成分
   • 例如，提取出信号的 低频成分（长期趋势）和 高频成分（周期波动）。
4. 选择有用成分：根据需要，选择最能反映数据特征的成分，去除无关噪声。

举例：假设你在分析股票价格的波动。SSA可以帮助你从复杂的股市波动中提取出：

• 长期趋势（例如股市上涨或下跌的趋势），
• 周期性波动（例如股市在某个周期内的涨跌波动），
• 以及 随机噪声（例如股市的突发性变化）。

经验模态分解（EMD）

核心功能：EMD是一种 自适应 的时序分解方法，通过不断提取时间序列中的 本征模态函数（IMF） 和 趋势项，分解出多尺度的信号成分。EMD特别适用于非线性和非平稳的数据，能够动态适应数据的频率变化。

算法流程：

1. 局部极值提取：首先从时间序列中提取局部的极大值和极小值，然后通过这两个极值拟合出上下包络线。
2. 计算局部均值：上下包络线的平均值即为当前信号的局部均值。
3. 去除均值：将当前信号减去局部均值，得到 本征模态函数（IMF），这部分信号是频率较高的成分。
4. 迭代过程：从原始数据中去除该IMF后，剩下的部分继续进行同样的过程，直到剩余部分为一个趋势项，即频率较低的成分。
5. 分解完成：最终会得到若干个本征模态函数（IMF）和一个趋势项。

举例：假设你正在分析海洋波浪的数据。EMD能够帮助你将波浪信号分解成多个 频率不同的成分，其中：

• 高频部分可能代表了快速波动（例如海面的小波动），
• 低频部分代表了较大的趋势变化（如潮汐的变化）。

方法	核心功能	适用场景	优点	缺点
STL	基于Loess回归分解为趋势、季节性、残差。	季节性明显的时间序列（如气温、销售数据）。	对非线性趋势和季节性变化自适应，灵活。	对噪声敏感，可能导致过拟合。
SSA	通过奇异值分解提取周期性和趋势成分。	存在周期性波动的时间序列。	对周期性信号提取强大，有较好去噪效果。	对窗口选择敏感，计算复杂度高。
EMD	自适应分解为多个本征模态函数（IMF）和趋势项。	非线性、非平稳信号（如复杂的自然现象）。	可以处理复杂的非线性信号，灵活。	计算复杂，可能存在伪模态和端点效应。

时序分割

一般就常识而言，每个设备都有好几种运行的工况，在不同工况下，其数据特点可能是明显不同的，有的时候是存在明确的划分规则的，但是有的却没有细分或者就是自然运行产生的，为此希望通过数据中找到一定的规律，自动挖掘其阶段变化的分割点，这里会阐述3种经典的分割方式：Changpoint、TreeSplit、Autoplait

Changpoint

核心功能：Changpoint 方法主要用于时间序列数据的变化点检测。它的目标是找出时间序列中存在的结构变化点（例如数据分布、趋势或周期的变化），这些变化点通常表示系统运行状态的改变。在许多工程和物理系统中，不同的运行工况可能导致数据的统计特性发生变化，Changpoint 就是帮助识别这些变化点。

实现流程：

• 数据预处理：首先对原始时间序列进行预处理，包括去噪、平滑等操作。
• 变化点检测：通过统计方法检测序列中潜在的变化点。常见的方法包括：
  • AMOC (Adaptive Monitoring of Change): AMOC 基于滑动窗口和统计检验来检测数据中的突变点，适用于实时监控。
  • SegNeigh：基于邻域分割的策略，通过对时间序列数据进行分段，找出变化点的位置。
• 优化与验证：通常通过最小化误差或通过交叉验证来优化模型，确保所找到的变化点能够有效分割不同工况阶段。

举例：假设有一个生产设备的振动数据，随着工况的变化，振动频率会发生明显的改变。使用 Changpoint 方法，系统可以自动识别出不同的运行工况变化点。例如，在设备启动时，振动数据波动较大，而当设备稳定运行时，波动幅度明显减小，系统会通过 AMOC 方法发现这些变化，并自动划分为不同的阶段。

TreeSplit

核心功能：TreeSplit 方法通过对数据进行符号化处理，将连续的时间序列数据转化为离散的符号序列，然后利用特征提取和聚类算法识别不同的阶段。其主要优势是能够在数据具有复杂变化模式的情况下，自动从中提取出潜在的阶段性结构。

实现流程：

• 数据符号化：首先通过 HOG（Histogram of Oriented Gradients，方向梯度直方图）方法将时间序列的每个时间点转换为一个符号或类别。这一过程将连续的信号转换为离散的特征符号，简化数据的表示。
• 窗口特征提取：然后，将时间序列按窗口划分，提取每个窗口中的特征。例如，可以提取每个窗口内的统计量，如均值、方差等。
• 聚类：基于窗口特征，使用聚类算法（如GMM）对窗口进行聚类，从而确定时间序列中的不同阶段。聚类结果将帮助标定不同的运行阶段或工况。

举例：假设有一个电机的电流信号，电流信号在不同工况下会呈现不同的变化模式。通过 TreeSplit 方法，首先将电流信号的每个数据点用 HOG 方法转化为一个符号，然后按时间窗口提取出每个窗口内的特征（如均值、最大值等），再通过聚类算法发现电流信号的不同模式。最终，系统将自动将整个电流信号分割为多个阶段，例如启动阶段、稳态阶段和关停阶段。

Autoplait

核心功能：Autoplait 方法通过隐马尔可夫模型（HMM） 和 最小描述长度（MDL） 准则自动分割时间序列数据。它的核心思想是使用隐马尔可夫模型建模时间序列的不同阶段，并通过最小描述长度原则选择最优的分割点，使得模型在描述数据时的复杂度最小。

实现流程：

• HMM 建模：首先使用隐马尔可夫模型（HMM）对时间序列进行建模。HMM 可以用来描述不同阶段之间的转移关系，每个隐状态代表时间序列的一个阶段。
• 最小描述长度（MDL）：在模型训练过程中，Autoplait 通过最小描述长度原则来选择合适的模型参数。MDL 旨在寻找能够有效描述数据的模型，同时避免过拟合。通过对比不同分割方案的描述长度，选择最能描述数据结构的分割点。
• 自动分割：根据 HMM 模型和 MDL 原则，系统自动识别并分割时间序列中的不同阶段。

举例：假设我们有一个设备的温度监测数据，目标是根据这些数据自动分割出设备的不同工作阶段（例如启动、运行、关停等）。数据如下：

时间	温度
0	25
1	30
2	50
3	60
4	58
5	40
6	30

在这个例子中，设备温度在时间 t=2 时发生了变化，假设在 t=0-2 是启动阶段，t=3-5 是运行阶段，t=6 是关停阶段。

步骤 1：HMM 建模：

• Autoplait 会基于温度数据，假设有三个隐状态：S1（启动），S2（运行），S3（关停）。
• 对于每个状态，HMM 会估计对应的温度分布（例如，高斯分布），并且会估计隐状态之间的转移概率。

步骤 2：MDL 评估分割点

• Autoplait 会尝试不同的分割点，假设试验以下两种分割：
  • 方案 1：将数据分为两个阶段，分别是：S1（启动阶段）和 S2（运行阶段）。从 S2 到 S3 的转移发生在 t=5。
  • 方案 2：将数据分为三个阶段，分别是：S1（启动阶段），S2（运行阶段），S3（关停阶段）。从 S1 到 S2 的转移发生在 t=2，从 S2 到 S3 的转移发生在 t=5。
• Autoplait 会为每种分割方案计算其 模型复杂度和 数据拟合误差：
  • 方案 1：模型较简单，只有两个阶段，转移较少，但拟合误差可能较大。
  • 方案 2：模型较复杂，有三个阶段，拟合误差可能较小，但模型复杂度较高。

步骤 3：选择最佳分割点

• 计算每种分割方案的 描述长度（包含模型复杂度和拟合误差）。
• 描述长度较小的方案会被选为最终的分割方案。

最终，Autoplait 会选择 描述长度最小的分割点，假设是方案 2（即在 t=2 和 t=5 进行分割），那么它就会将时间序列分为 启动、运行、关停 三个阶段。

有价值的辅助

时序分割实则属于无监督学习，聚类结果依赖于样本分布和距离函数定义，若产生有意义的结果一般会有以下5种方法

• 提供手工标记：针对一个典型数据集合，人工打标模式
• 典型模式样本库：算法根据其匹配相似度进行发掘
• 改变样本分布：多提供感兴趣的区域样本
• 业务知识粗分区：在每个分区进行细分聚类
• 信号分解算法：将原始的时序数据进行分解，对主要成分进行模式聚类

时序再表征

对于高维数据，中间混杂着噪声和无关紧要的数据，为数据挖掘算法带来了一定的干扰，因此需要将原始数据进行再表征并降低维度。下图是一些时序再表征的方法，最上面第一个曲线是原始曲线，第二个曲线是时序再表征后的曲线，而下面陈列的是不同特征组成的曲线。

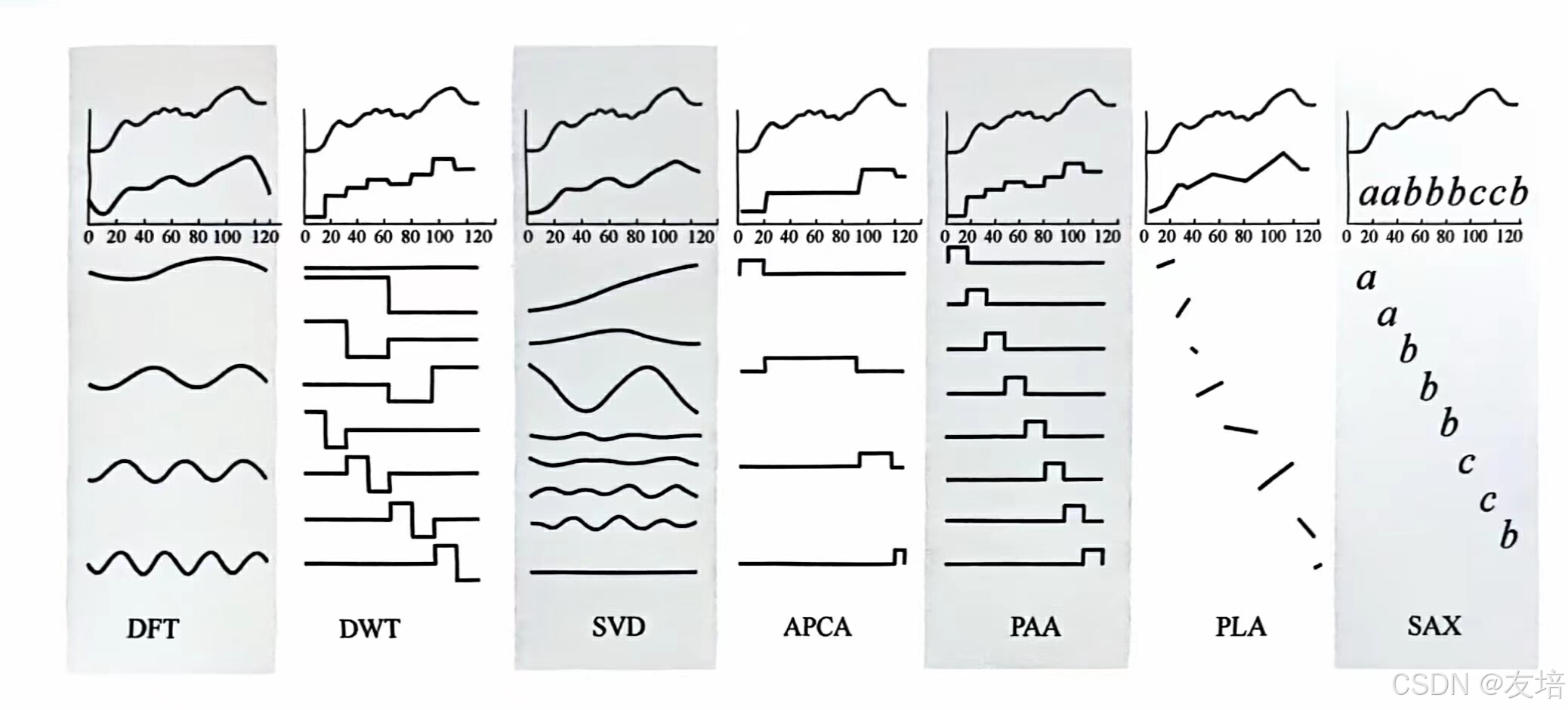
再表征算法的介绍和示例

算法	核心功能	示例
PAA (Piecewise Aggregate Approximation)	PAA通过将时间序列划分为若干等长段，每段取该段的平均值来简化序列，达到数据降维的效果。这种方法可以有效减少数据点的数量，从而降低计算复杂度，适用于大规模数据分析和快速处理。	将温度传感器数据每5分钟取一次温度，按每小时的数据段取平均值表示，得到简化后的时间序列。
PLA (Piecewise Linear Approximation)	PLA通过将时间序列分成若干段，并用线性段来逼近每段数据，保留数据的趋势变化。相比PAA，PLA能够更好地近似数据的变化模式，但计算复杂度较高。	用直线段拟合股票价格的波动趋势，每个线段对应价格变化的一部分，捕捉价格波动的走向。
PIP (Piecewise Information Preserving)	PIP方法通过分段，每段选择具有代表性的信息点，从而最大限度地保留时间序列中的关键信息。它能更精确地保留数据的特征，适用于对数据精度有较高要求的任务。	对心电图(ECG)信号进行分段，每段选取最具代表性的数据点，以保留信号的关键信息。
SMA (Simple Moving Average)	SMA通过滑动窗口计算时间序列中每个数据点及其周围点的平均值，起到平滑波动的作用。它主要用于去除噪声并突出长期趋势，适用于稳定的数据。	对每日气温数据使用3天滑动平均进行平滑，去除短期波动，显示长期趋势。
Auto Encoder	Auto Encoder是基于神经网络的模型，通过编码器将输入数据压缩到低维空间，再通过解码器重建原始数据。它能够学习数据中的潜在特征，广泛用于复杂数据的降维和异常检测。	对手写数字图像数据进行降维，通过自编码器提取低维特征并重建图像，进行数字识别。