序列模型的使用示例
- 1 RNN原理
- 1.1 序列模型的输入输出
- 1.2 循环神经网络(RNN)
- 1.3 RNN的公式表示
- 2 数据的尺寸
- 3 PyTorch中查看RNN的参数
- 4 PyTorch中实现RNN
- (1)RNN实例化
- (2)forward函数
- (3)多层RNN的参数尺寸
- 5 实战
1 RNN原理
1.1 序列模型的输入输出
假如你想要建立一个序列模型,它的输入语句是这样的: “Harry Potter and Herminoe Granger invented a new spell.”,(句中的人名都是出自于 J.K.Rowling 笔下的系列小说 Harry Potter)。假如你想要建立一个能够自动识别句中人名的序列模型,那么这就是一个命名实体识别问题。命名实体识别系统可以用来查找不同类型的文本中的人名、公司名、时间、地点、国家名和货币名等等。
将输入的句子定义为x,上述的输入语句中共有9个单词,可以对输入进行编号,用
x
<
t
>
x^{<t>}
x<t> 来索引句子中第t个单词的位置。假如这个序列模型有一个输出序列,使得输入的每个单词都对应一个输出值,这个值为1表示对应的输入单词是人名的一部分,为0表示不是人名的一部分,同时用
y
<
t
>
y^{<t>}
y<t> 对输出进行编号,如下图所示:

同时我们用 T x T_x Tx 来表示输入序列的长度,这个例子中输入是9个单词,所以 T x = 9 T_x= 9 Tx=9 ,同样,可用 T y T_y Ty 来表示输出序列的长度。输出序列的长度可以和输入序列的相同,也可以不同。
之前我们在DNN中用
x
(
i
)
x^{(i)}
x(i) 表示第i个训练样本,这里我们可以用
x
(
i
)
<
t
>
x^{(i)<t>}
x(i)<t> 来表示第i个样本的第t个元素,
T
x
(
i
)
T{x}^{(i)}
Tx(i) 代表第i个训练样本的输入序列长度。同样的,用
y
(
i
)
<
t
>
y^{(i)<t>}
y(i)<t> 来表示第i个样本的第t个元素对应的输出值,
T
y
(
i
)
T{y}^{(i)}
Ty(i) 代表第i个训练样本的输出序列长度。
我们该怎样表示序列中的一个单词呢,比如Harry这个单词,对应的索引
x
(
1
)
x^{(1)}
x(1) 是什么?自然语言处理(Natural Language Process,简称NLP)中,想要表示一个句子里的单词,第一件事是做一张词表,有时也称为词典,我们这里用10000个单词的词典举例。

当词典构建好之后,遍历数据集,给数据集中的每一个单词匹配一个one-hot编码,即用一个10000维的向量表示,例如单词a出现在词典中的第一个位置,那么当输入a时,就生成一个10000维的向量,该向量的第一个元素是1,其他都是0。
因此,给定上述输入语句,可以生成如下的向量:

图中其实就是One-hot向量,因为向量中只有一个位置是1,其余都是0。
如果遇到不在词典中的单词,那么就创建一个叫做 Unknow Word 的伪单词,用<UNK>作为标记,来表示不在词表中的单词。
这里我们用的词典只有一万个单词,正常商业应用的词典,词汇量3万至5万比较常见,10万的也有,某些大型互联网公司用的词典,其单词数量甚至超过百万。
1.2 循环神经网络(RNN)
这节我们来谈一谈怎样建立模型,来实现从X到Y的映射。
我们先尝试一下标准神经网络。前面的例子,“Harry Potter and Herminoe Granger invented a new spell.”有9个单词,因此需要把这9个单词一次性输入网络,如图所示:

为了方便输入,可以将单词索引成一个整数,但使用标准神经网络有以下两个问题:
- 上述例子是9个单词,所以输入单元是9个,但如果另一条句子有10个单词,那么这张网络将不再适用。
- 这种网络并不共享从文本的不同位置上学到的特征。具体来说,经过训练后的神经网络,当Harry出现在位置 x < 1 > x^{<1>} x<1> 时,会将其判定为人名的一部分,那么如果Harry 出现在其他位置,比如 x < 8 > x^{<8>} x<8> 时,很有可能因为位置不同,权重参数不同,神经网络不会将其认为是人名的组成部分。
为了解决上述问题,这里引入循环神经网络的概念。
还是“Harry Potter and Herminoe Granger invented a new spell.”这句话,如果从左往右逐个读取单词,当读到第一个单词Harry时,将其对应的One-hot向量 x < 1 > x^{<1>} x<1> 输入到神经网络,输出 y ^ < 1 > \hat{y} ^{<1>} y^<1>,并判断其是否为人名的一部分,用下面的图表示:

这里只有两层神经网络,一个隐藏层(图中的小圆圈可以认为是神经元),一个输出层。设隐藏层的激活值为 a < 1 > a^{<1>} a<1> ,输入第一个单词的过程称为时间步1。
接着读取第二个单词,将 x < 2 > x^{<2>} x<2> 输入神经网络, x < 2 > x^{<2>} x<2> 乘以权重之后,并不是马上激活,而是要先加上来自时间步1的激活值 a < 1 > a^{<1>} a<1>,然后再将相加后的结果激活,获得激活值 a < 2 > a^{<2>} a<2> ,最后计算输出层,获得预测值 y ^ < 2 > \hat{y} ^{<2>} y^<2>。(这样说不太准确,但这样说方便理解,后面会详细讲解)
依此类推,在计算激活值的时候,加入上一时步的激活值,直至整条语句读取结束,这就是循环神经网络,结构如下:

为了使各个部分结构一致,在零时刻,需要构造一个激活值
a
<
0
>
a^{<0>}
a<0> ,这通常是个零向量,加上激活值
a
<
0
>
a^{<0>}
a<0> 后的结构如下图所示:

在某些文献中,你看到的循环神经网络有可能是下面这种形式:

在每一个时间步中,输入 x < t > x ^{<t>} x<t> 输出 y < t > y ^{<t>} y<t> ,用一个带箭头的圆圈,表示把激活值重新输入网络,圆圈上面加上一个方块,表示激活值输回网络会延迟一个时间步。
循环神经网络每个时间步的参数也是一致的,也就是说,第一次输入时的网络和第二次、第三次、第t次输入时,网络的参数完全一致。
因为只有一个隐藏层,因此我们设隐藏层的权重参数为Wax,各个时步的Wax相同。我们设水平联系的权重参数为Waa,在计算本时步激活值的时候,把上一层的激活值乘以Waa,然后再加到本时步,各个时步的Waa相同。本时步的激活值算出来之后,需要计算输出值,这时需要乘以一个输出权重Wya,再将结果激活作为输出值。Wax、Waa、Wya这些参数,第一个下标表示用来计算什么,第二个下标表示这个参数该乘什么。
将以上参数标在图片中,则是下面这个结果:

标在简化循环图中,则是下面的结果:

1.3 RNN的公式表示
如果把上面的过程用公式表达,则如下所示:
a
<
1
>
=
g
(
W
a
a
a
<
0
>
+
W
a
x
x
<
1
>
+
b
a
)
y
<
1
>
=
g
(
W
y
a
a
<
1
>
+
b
y
)
\begin{array}{l} a^{<1>}=g\left(W_{a a} a^{<0>}+W_{a x} x^{<1>}+b_{a}\right) \\ y^{<1>}=g\left(W_{y a} a^{<1>}+b_{y}\right) \end{array}
a<1>=g(Waaa<0>+Waxx<1>+ba)y<1>=g(Wyaa<1>+by)
这里面g表示激活函数,一般情况下,隐藏层使用tanh作为激活函数,有时也用Relu,输出层看网络要解决的问题,如果是二分类问题,就用sigmoid,如果是k分类问题,就用softmax。如果想区分隐藏层和输出层的激活函数,那么可以对g标号,如下所示:
a
<
t
>
=
g
1
(
W
a
a
a
<
t
−
1
>
+
W
a
x
x
<
t
>
+
b
a
)
y
<
t
>
=
g
2
(
W
y
a
a
<
t
>
+
b
y
)
\begin{array}{l} a^{<t>}=g_1\left(W_{a a} a^{<t-1>}+W_{a x} x^{<t>}+b_{a}\right) \\ y^{<t>}=g_2\left(W_{y a} a^{<t>}+b_{y}\right) \end{array}
a<t>=g1(Waaa<t−1>+Waxx<t>+ba)y<t>=g2(Wyaa<t>+by)
其中,计算激活值的公式可以简化表示如下:
a
⟨
t
⟩
=
g
1
(
W
a
[
a
⟨
t
−
1
⟩
,
x
⟨
t
⟩
]
T
+
b
a
)
a^{\langle t\rangle}=g_{1}\left(W_{a}\left[a^{\langle t-1\rangle}, x^{\langle t\rangle}\right]^{T}+b_{a}\right)
a⟨t⟩=g1(Wa[a⟨t−1⟩,x⟨t⟩]T+ba)
这里
W
a
=
[
W
a
a
,
W
a
x
]
W_{a}=\left[W_{a a}, W_{a \mathrm{x}}\right]
Wa=[Waa,Wax]。
假设单词库里有一万个单词,那么 x < t > x^{<t>} x<t> 的维度为(10000, 1),若隐藏层有100个神经元,那么 a < t > a^{<t>} a<t> 的维度为(100, 1), [ a < t − 1 > , x < t > ] T \left[a^{<t-1>}, x^{<t>}\right]^{T} [a<t−1>,x<t>]T 的维度为(10100, 1)。Waa的维度就是(100,100),Wax的维度就是(100,10000),把这两个矩阵整合之后,Wa就是(100,10100)。
同样对于输出层的公式,也可以使用更简单的方式重写:
y
<
t
>
=
g
2
(
W
y
a
<
t
>
+
b
y
)
y^{<t>}=g_{2}\left(W_{y} a^{<t>}+b_{y}\right)
y<t>=g2(Wya<t>+by)
现在
W
y
W_y
Wy 和
b
y
b_y
by、
W
a
W_a
Wa 和
b
a
b_a
ba,下标表示的是分别会输出什么类型的量。
使用上述记法,当我们建立更复杂模型时就能够简化我们要用到的符号。
如果将循环神经网络的结果画得更工整一点,将是下面的图形:

这种结构的循环神经网络有一个缺点,就是在计算t时步时,仅仅使用了t时步以前的计算结果,没有使用t时步之后的结果。比如,现在有两个句子,“Teddy Roosevelt was a great President.”(中文意思是 西奥多罗斯福是一位伟大的总统,因为他的小名也叫泰迪,因此也经常被称为“Teddy Roosevel”),“Teddy bears are on sale!”(正在销售泰迪熊),如果使用相同的循环神经网络从左往右扫描句子,那么获得的第一个单词都是Teddy,因为是第一个,都没有从上一层传过来的激活值,那么会获得相同的输出,前者Teddy是人名,后者是熊,因此两者的输出,必有一个有错。
针对这个问题,可以使用双向循环神经网络。不过本文的重点是RNN的原理和过程,以及在PyTorch中的数据处理,目的是了解这一类模型的调用的和数据处理方式,讲原理只是为了后面讲接口时能更直观。
2 数据的尺寸
这里先说明一下,本节的资料来源和上节不一样,因此符号定义和上面的有所不同,了解原理即可。
RNN每次输入一个单词,那么
x
t
x_t
xt 就是该单词对应的One-hot向量,尺寸为[vector_length]或[1,vector_length],向量长度也是特征长度,因此也可以用[feature len]或者[1, feature len]来表示。
使用PyTorch的并行技术,给模型喂数据的时候,每次都喂一个batch。假设每个batch由5个句子各出一个单词组成,则batch_size=5,那么就相当于有5条生产线(这5条生产线共享参数),每次喂数据的时候,都是给这5条生产线各喂一个单词,所以
x
t
x_t
xt 的尺寸为[batch_size, vector_length]。
如果觉得每次输入一个单词太慢,那么可以一次输入, 假如每条句子都是8个单词,那么x的尺寸是[8, 5, feature len],如果每次输入的单词个数是seq len,那么x的尺寸是[batch_size, seq len, feature len],seq len表示句子长度。
为了便于探讨RNN中参数的尺寸,下面我们不对输出层加激活函数,假设第t时步的计算过程如下图所示:

这里 W x h W_{xh} Wxh 、 W h h W_{hh} Whh 、 W h y W_{hy} Why ,第一个下标表示这个参数该乘什么,第二个下标表示这个参数用来计算什么,和前面介绍原理时刚好相反。
上图中
x
t
x_t
xt 是每个时步输入的数据,它的尺寸是[batch_size, feature len],假设隐藏层的神经元个数为hidden length,那么隐藏层的输出
h
t
h_t
ht 的尺寸就是[batch_size, hidden len]。
那么
W
x
h
W_{xh}
Wxh 参数的尺寸为[feature len, hidden len],它的意义是压缩数据的维度,将
x
t
x_t
xt 的特征长度由feature len压缩为hidden len。
因为循环神经网络每个时间步的参数一致,所以
h
t
−
1
h_{t-1}
ht−1 的尺寸也为[batch_size, hidden len],
h
t
−
1
W
h
h
h_{t-1} W_{h h}
ht−1Whh 的尺寸要和
x
t
W
x
h
+
b
h
x_{t} W_{x h}+b_{h}
xtWxh+bh 的一致,因此
W
h
h
W_{hh}
Whh 的尺寸为[hidden len, hidden len]。
一般情况下,
y
t
y_t
yt 的特征长度为1,因此其尺寸为[batch_size, 1],那么
W
h
h
W_{h h}
Whh 的尺寸为[hidden len, 1]。
3 PyTorch中查看RNN的参数
import torch
import torch.nn as nn
model = nn.RNN(input_size=10, hidden_size=5, num_layers=1)
'''循环层的输入是10,即表示输入数据对应的One-hot向量长度是10,
隐藏层里有5个元素,循环层有1层'''
print(model) # 打印网络的结构
print(model._parameters.keys()) # 打印参数结构
'''打印参数的尺寸'''
print('----------------------------------------')
print(model.weight_ih_l0.size()) # W_xh.T
print(model.weight_hh_l0.size()) # W_hh.T
print(model.bias_hh_l0.size())
print(model.bias_ih_l0.size())
'''参数名的末尾l0表示第0层,0 layer'''
'''如果RNN有3层,那么会有l0,l1,l2'''
输出
RNN(10, 5)
odict_keys(['weight_ih_l0', 'weight_hh_l0', 'bias_ih_l0', 'bias_hh_l0'])
----------------------------------------
torch.Size([5, 10])
torch.Size([5, 5])
torch.Size([5])
torch.Size([5])
上面这段程序有几点需要注意:
1 model.weight_ih_l0并不是
W
x
h
W_{xh}
Wxh,而是
W
x
h
T
W_{xh}{ }^{T}
WxhT,即是转置后的结果。
2 隐藏层使用的结构是这样的:
h
t
=
tanh
(
x
t
W
x
h
+
b
x
h
+
h
t
−
1
W
h
h
+
b
h
h
)
h_{t}=\tanh \left(x_{t} W_{x h}+b_{x h}+h_{t-1} W_{h h}+b_{h h}\right)
ht=tanh(xtWxh+bxh+ht−1Whh+bhh),我们一般写式子的时候,常常把
b
x
h
b_{x h}
bxh 和
b
h
h
b_{h h}
bhh 合并成
b
h
b_{h}
bh 。
3 上面的model中,没有计算
y
t
y_t
yt 的模块,如果需要计算
y
t
y_t
yt 的模块,需要增加一个线性层模块(见实战环节)。
4 PyTorch中实现RNN
(1)RNN实例化
调用nn.RNN可以创建RNN模型,它的__init__有四个参数:
input_size,单词的编码长度
hidden_size,隐藏层的单元个数
num_layer,RNN的层数,默认为1
batch_first,表示batch_size这个维度是否在最前面,默认为False,False表示输入数据的结构是[seq len,batch_size,feature],为True则表示输入数据的结构是[batch_size,seq len,feature]
通过nn.RNN创建的RNN模型,没有线性层,需要自己手动添加。
因为我们习惯将batch_size维度放到最前面,下面的关于输入输出尺寸的讨论,都是在batch_first=True的情形下。
(2)forward函数
输入输出分别为
out, ht = forward(self, x, h0)
假如有3句话(三条生产线),每句话都有5个单词,单词用长度为100的向量来编码,那么x的尺寸为[3, 5, 100],RNN中,可以使用并行化技术,一次性把所有的x输入到RNN中,不需要一个单词一个单词地喂。
out是每个时间步的最后一个隐藏层的输出,尺寸为[batch_size, Seq len, hidden],其中Seq len是每句话的单词数量,比如可以是5。
无论RNN有多少层,out的尺寸都是[batch_size, Seq len, hidden],也就是说,RNN中各个隐藏层的神经元数量都是hidden。
ht是最后一个时间步的每一层的输出,尺寸为[batch_size, num_layers, hidden len],而第一个时间步由于没有上一轮的输入,因此第一时步使用h0,h0的尺寸也为[batch_size, num_layers, hidden len]。
(3)多层RNN的参数尺寸
rnn = nn.RNN(100, 10, 2, batch_first=True)实例化一个2层的RNN,2层指的是隐藏层数量,这个两层的模型,输入样本的特征长度为100,输出长度为10,那么第一层的输出数据的特征长度是多少?
每个时步第一层的输出的长度就是10,也就是说,多层RNN,在第一层就完成了数据的维度压缩。
5 实战
房价预测模型:已知某地区连续50个月的房价,根据已有数据,预测第51个月的房价。
使用RNN来预测,代码如下:
import numpy as np
import torch
from matplotlib import pyplot as plt
import torch.nn as nn
import torch.optim as optim
import torch.functional as F
'''房价预测模型'''
'''超参数'''
num_time_steps = 50 # 50个时步
input_size = 1 # 数据编码长度是1
hidden_size = 16 # 隐藏层有16个单元
output_size = 1 # 输出层只有1个单元
lr = 0.01 # 学习率是0.01
class Net(nn.Module):
def __init__(self, ):
super(Net, self).__init__()
'''循环层'''
self.rnn = nn.RNN(
input_size=input_size,
hidden_size=hidden_size,
num_layers=1,
batch_first=True,
)
'''batch_first默认为False,False表示输入数据的结构是[seq len,batch_size,feature],
为True表示输入数据的结构是[batch_size,seq len,feature]'''
'''参数初始化'''
# for p in self.rnn.parameters():
# nn.init.normal_(p, mean=0.0, std=0.001)
'''线性层'''
self.linear = nn.Linear(hidden_size, output_size)
def forward(self, x, hidden_prev):
out, hidden_prev = self.rnn(x, hidden_prev)
'''x的尺寸为[batch_size, seq len, feature len],
out的尺寸为[batch_size, seq len, hidden_size]'''
out = out.view(-1, hidden_size) # 打平的目的是为了送到线性层
'''这里假设标签是二维的,其尺寸为[50, 16]
为了让标签值和预测值能够进行比较,因此将out打平,打平后,50等效于“batch_size维度为50”'''
out = self.linear(out)
out = out.unsqueeze(dim=0) # 插入真正的batch_size维度
'''如果不插入一个新的维度,那么out的输出将变成[50, 1],
而在定义数据时,y被定义成了[1, 50, 1],因此需要插入一个新的维度'''
'''其实上面的步骤可以先不打平,而是先输入到线性层,输出的结果直接是[1,50,1]'''
return out, hidden_prev
'''需要注意的是,房价预测模型,其自变量不是月份,而是前面若干个月的房价,
也就是说,上述Net中的x,是房价,不是时间。
因此'''
model = Net()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr)
hidden_prev = torch.zeros(1, 1, hidden_size) # h0的初始值
# 训练
for iter in range(1000):
start = np.random.randint(3, size=1)[0]
'''从0,1,2里面随机抽取一个数,为什么要从3个数字里面抽一个?
因为如果每次都是从0开始,RNN很容易记住'''
time_steps = np.linspace(start, start + 10, num_time_steps)
data = np.sin(time_steps)
data = data.reshape(num_time_steps, 1)
x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)
'''由于前面实例化的时候,batch_first=True,这里将 x 和 y 重塑成[1, 49, 1]之后,
数据的batch_size = 1,但有49条生产线,房价可以有一个数来表征,因此feature len=1
'''
'''因为num_time_steps=50,因此有50个时步,所以data的下标是0-49,
data[:-1]表示从data[0]到data[48],
data[1:]表示从data[1]到data[49]
该算法的思路就是,根据第1天的房价(x[0])预测第2天的房价(output[0]),
再将其与第二天的真实房价y[0]进行对比,求出第一天的误差。
其他天的误差也是类似,最后根据前49天的房价x,求出从第2-50天的房价预测值,
利用第2-50天的房价真实值与预测值之间的误差,训练模型。
这就是为什么训练的时候 x 和 y 的长度是49的原因。
'''
output, hidden_prev = model(x, hidden_prev)
hidden_prev = hidden_prev.detach()
'''detach()的作用是脱离原来的计算图,使其不再需要梯度信息,这样参数反向传播
因为该算法每轮迭代都使用上一轮迭代的hidden_prev,如果hidden_prev不与原来的计算图脱钩,
那么求导的时候,会沿着hidden_prev进入上一轮迭代的计算图,这样就会报错,说视图在计算图上求两次导'''
loss = criterion(output, y)
model.zero_grad()
loss.backward()
# for p in model.parameters():
# print(p.grad.norm())
# torch.nn.utils.clip_grad_norm_(p, 10)
optimizer.step()
'''没迭代100次,输出一次'''
if iter % 100 == 0:
print("Iteration: {} loss {}".format(iter, loss.item()))
'''其实可以在每一轮循环的时候,都使用0作为hidden_prev,因为你不知道从什么位置开始,
所以无法估计出第-1时步的结果是多少,因此hiiden_prev选择什么值都是不完美的'''
# 预测房价的趋势
start = np.random.randint(3, size=1)[0]
time_steps = np.linspace(start, start + 10, num_time_steps)
data = np.sin(time_steps)
data = data.reshape(num_time_steps, 1)
x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)
predictions = []
input = x[:, 0, :]
hidden_prev = torch.zeros(1, 1, hidden_size)
'''只需要知道第一天的值,就能求得后面49天的房价'''
for _ in range(x.shape[1]):
'''循环49次,一个一个喂数据
将上一轮的输出(预测值)作为本轮的输入'''
input = input.view(1, 1, 1)
(pred, hidden_prev) = model(input, hidden_prev)
input = pred
'''将每一轮的输出存进列表'''
predictions.append(pred.detach().numpy().ravel()[0])
x = x.data.numpy().ravel()
y = y.data.numpy()
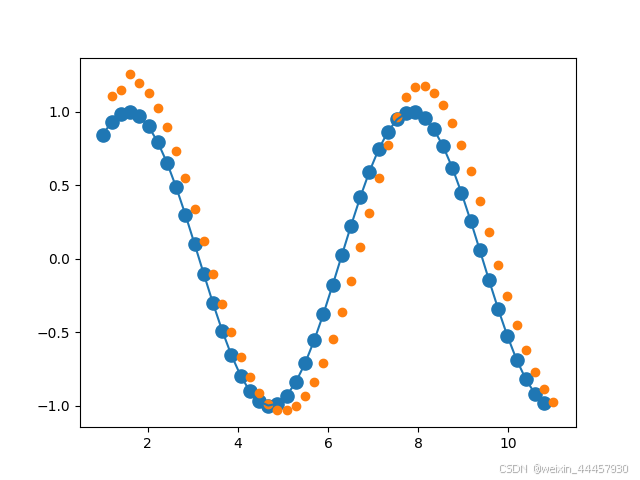
plt.scatter(time_steps[:-1], x.ravel(), s=90)
plt.plot(time_steps[:-1], x.ravel())
plt.scatter(time_steps[1:], predictions)
plt.show()
输出:
Iteration: 0 loss 0.8515104055404663
Iteration: 100 loss 0.0022286889143288136
Iteration: 200 loss 0.0038173357024788857
Iteration: 300 loss 0.004501968156546354
Iteration: 400 loss 0.0035968958400189877
Iteration: 500 loss 0.0017438693903386593
Iteration: 600 loss 0.002284669317305088
Iteration: 700 loss 0.0019050785340368748
Iteration: 800 loss 0.0011780565837398171
Iteration: 900 loss 0.00046253044274635613
显示