引言
分治思想是将问题分解为更小子问题,分别解决后再合并结果。二叉树中常用此思想,因其结构递归,易分解为左右子树问题,递归解决后合并结果。
这篇文章会讲解用分治的思想去解决二叉树的一些题目,顺便会强调在做二叉树的题过程中我容易出错的地方。
单值二叉树:力扣965
我们来看一个题目,这个题就用到了分治的思想:
题目链接:965. 单值二叉树 - 力扣(LeetCode)

要想检查一棵树里所有节点的值是否相等,最简单的方式是把每个节点挨个挨个遍历一遍,看看每个节点的值是否与孩子节点(孩子节点不为空的情况下)的值相等。但是这就没有用到分治的思想了。
如何通过分治的思想来解决问题呢?把大问题拆成很多个小问题。求一棵树里所有节点的值是否相等(大问题),就是求左右子树里节点的值是否与根节点的值相等(小问题)。
bool isUnivalTree(struct TreeNode* root) {
if(root==NULL){
return true;
}
if((root->left&&root->val!=root->left->val)||(root->right&&root->val!=root->right->val))
{
//检查左右孩子的值是否与根的值相等
return false;
}
return isUnivalTree(root->left)&&isUnivalTree(root->right);
}二叉树的前序遍历:力扣144
如果学过二叉树的基础知识掌握的比较好,那它的前序遍历对你来说就是小菜一碟。那为什么这里还要把它拿出来讲解呢?我们先来看一下这道题:144. 二叉树的前序遍历 - 力扣(LeetCode)
我们发现,这道题比我们平时实现的二叉树的前序遍历又额外提了一个要求:将节点的值按照前序遍历的顺序存放在数组中,并将这个数组作为返回值返回。
额外补充一句:在力扣中,如果要求我们返回数组,那我们需要记录它的数组大小。在这个题中,preOrderTraversal函数中的第二个参数returnSize记录的就是最后要返回数组的大小。
分析
其实,只要掌握了二叉树的前序遍历,就算是把里面节点的值按照前序遍历的顺序存放在数组中也不难,但是里面我们有些点需要注意:
首先,我们需要先计算出二叉树中有几个节点,这样我们才好根据节点个数来开辟数组。
附上代码:
int treeSize(struct TreeNode* root)
{
if (root == NULL) {
return 0;
}
return treeSize(root->left) + treeSize(root->right) + 1;
}需要注意的问题
然后,我们要再弄一个进行前序遍历的函数,每遍历到一个节点就把它存进数组。
易错代码:
void preOrder(struct TreeNode* root,int* a,int i)
{
if(root==NULL){
return;
}
a[i++]=root->val;
preOrder(root->left,a,i);
preOrder(root->right,a,i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
int size=treeSize(root),i=0;
int* a=(int*)malloc(sizeof(int)*size);
preOrder(root,a,i);
*returnSize=i;
return a;
}这段代码中存在一些问题,特别是在递归函数 preOrder 中对索引 i 的处理上。
问题分析:
1.索引传递问题: 在 preOrder 函数中,索引 i 是以值传递的方式传递的。这意味着每次递归调用 preOrder 时,都会创建一个新的 i 的副本,而这个副本在递归调用结束后就会被销毁。因此,递归调用中的 i++ 操作并不会影响到外层调用中的 i 值。
举个例子,当 preOrder 第一次被调用时,i 的值是 0。在将根节点的值存入数组后,i 被增加到 1,但这个增加的 i 只在当前函数栈帧中有效。当递归调用左子树或右子树时,i 又会重新从 0 开始,这显然是不正确的。
2.数组大小问题: 虽然数组 a 的大小是通过 treeSize 函数正确计算出来的,但由于索引传递的问题,最终可能并不会填满整个数组。实际上,由于每次递归调用都使用了一个新的 i 副本,所以可能只会在数组的第一个位置存储值。
3.返回大小问题: 由于索引 i 没有正确传递和更新,*returnSize 最终会被设置为一个错误的值。这意味着调用者无法知道实际存储了多少个节点值。
解决方案:
要解决这个问题,需要确保索引 i 在递归调用中能够正确传递和更新:
- 使用指针传递索引:将 i 的地址传递给 preOrder 函数,这样函数就可以直接修改 i 的值了。
有些人会想到用静态变量或全局变量的做法,但是这里不推荐,这种方法虽然可以工作,但会使函数变得不那么通用和可重用。
正确代码:
void preOrder(struct TreeNode* root,int* a,int* pi)
{
if(root==NULL){
return;
}
a[(*pi)++]=root->val;
preOrder(root->left,a,pi);
preOrder(root->right,a,pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
int size=treeSize(root),i=0;
int* a=(int*)malloc(sizeof(int)*size);
preOrder(root,a,&i);
*returnSize=i;
return a;
}二叉树遍历:牛客KY11
题目链接:二叉树遍历_牛客题霸_牛客网
这个题目要求我们根据一串二叉树先序遍历字符串建立链式存储的二叉树,其中#代表该节点为空节点。
分析
我们先根据题目中给出的示例1将二叉树还原出来:abc##de#g##f###
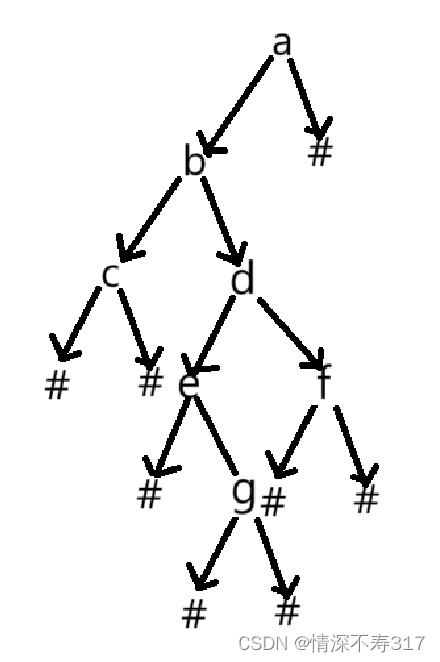
结合还原的过程,我们看一下如何通过遍历前序遍历字符串来还原二叉树:
先序遍历的特点是“根左右”,即先访问根节点,再访问左子树,最后访问右子树。
当我们遍历前序遍历字符串时,遇到 # 则返回 NULL,否则创建新节点并递归构建左右子树。
但这里有一个点需要注意,与上一道题中遍历数组时更新索引是一个问题。为了保证索引的正确传递和更新,我们需要往函数中传入索引的地址。
附上代码:
#include <stdio.h>
typedef struct binaryTreeNode{
struct binaryTreeNode* left,*right;
char val;
}BTNode;
BTNode* createTree(char* a,int* pi)
{
if(a[(*pi)]=='#'){
(*pi)++;
return NULL;
}
BTNode* node=(BTNode*)malloc(sizeof(node));
if(node==NULL){
perror("malloc fail");
return NULL;
}
node->val=a[(*pi)++];
node->left=createTree(a, pi);
node->right=createTree(a, pi);
return node;
}
void inOrder(BTNode* root)
{
if(root==NULL){
return;
}
inOrder(root->left);
printf("%c ",root->val);
inOrder(root->right);
}
int main() {
char a[100];
scanf("%s",a);
int i=0;
BTNode* tree=createTree(a, &i);
inOrder(tree);
return 0;
}



















