代码随想录day01--数组

两数之和

题目

地址：https://leetcode.cn/problems/two-sum/

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

示例:

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9

所以返回 [0, 1]

代码(核心代码模式)

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int res[] = new res[2];
        if(nums == null || nums.length == 0){
            return res;
        }
        Map<Integer,Integer> map = new HashMap<>();
        for(int i=0;i<nums.length;i++){
            int temp = target - nums[i];
            if(map.containsKey(temp)){
                res[0] = map.get(temp);
                res[1] = i;
                break;
            }
            map.put(nums[i],i);
        }
        return res;
    }
}

二分查找

题目

地址：https://leetcode.cn/problems/binary-search/

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

二分查找最关键的是要找到边界条件：即分为两种边界一种是左闭右闭区间，一种是左闭右开区间、

而针对第一种情况，left == right是有意义的，因此在定义right时，是right = nums.length - 1;并且在循环条件里要使用while(left<=right)

在这里插入图片描述

而第二种情况：left == right是每有意义的，因此在定义right时，是right = nums.length;并且在循环条件里要使用while(left<right)：即下一个目标值不会进行比较

在这里插入图片描述

代码

使用左闭右闭区间方法

class Solution {
    public int search(int[] nums, int target) {
        //先进行防御性编程
        if(target < nums[0] || target > nums[nums.length - 1]){
            return -1;
        }
        int left = nums[0],right = nums.length-1;
        while(left <= right){
            int mid = (left + (right-left >> 1));
            if(nums[mid] == target){
                return mid;
            }else if(nums[mid] > target){
                right = mid - 1 ;
            }else {
                left = mid + 1;
            }
        }
        return -1;
    }
}

2.使用左闭右开区间方法

class Solution {
    public int search(int[] nums, int target) {
        //先进行防御性编程
        if(target < nums[0] || target > nums[nums.length - 1]){
            return -1;
        }
        int left = nums[0],right = nums.length;
        while(left < right){
            int mid = (left + (right-left >> 1));
            if(nums[mid] == target){
                return mid;
            }else if(nums[mid] > target){
                right = mid;
            }else {
                left = mid + 1;
            }
        }
        return -1;
    }
}

移除元素

题目

地址：https://leetcode.cn/problems/remove-element/

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。

代码

使用双指针方法可以快速移除元素，在数组中内存空间是连续的，因此不是删除元素而是覆盖元素

使用双指针同向法

class Solution {
    public int removeElement(int[] nums, int val) {
        int slowIndex = 0;
        for(int fastIndex = 0; fastIndex<nums.length;fastIndex++){
            if(nums[fastIndex] != val){
                nums[slowIndex] = nums[fastIndex];
                slowIndex++;
            }
        }
        return slowIndex;
    }
}

使用双指针相向法

class Solution {
    public int removeElement(int[] nums, int val) {
        int leftIndex = 0,rightIndex = nums.length - 1;
        while(leftIndex <= rightIndex){
            if(nums[leftIndex] == val){
                nums[leftIndex] = nums[rightIndex];
                rightIndex--;
            }else{
                leftIndex++;
            }
        }
        return leftIndex;
    }
}

有序数组的平方

题目

地址：https://leetcode.cn/problems/squares-of-a-sorted-array/

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

最基本的排序就可以完成

双指针 也是很好的选择：

数组其实是有序的，只不过负数平方之后可能成为最大数了。

那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。

此时可以考虑双指针法了，i指向起始位置，j指向终止位置。

定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置。

如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。

如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。

如动画所示：

代码

使用最简单的排序算法就可以实现

class Solution {
    public int[] sortedSquares(int[] nums) {
        for(int i=0;i<nums.length;i++){
            nums[i] = nums[i] * nums[i];
        }
        Arrays.sort(nums);
        return nums;
    }
}

使用双指针算法也可以实现

class Solution {
    public int[] sortedSquares(int[] nums) {
        int left = 0,right = nums.length - 1;
        int[] Result = new int[nums.length];
        int index = Result.length - 1;
        while(left<=right){
            if(nums[left]*nums[left]<nums[right]*nums[right]){
                Result[index--] = nums[right]*nums[right];
                --right;
            }else{
                Result[index--] = nums[left]*nums[left];
                ++left;
            }
        }
        return Result;
    }
}

长度最小的子数组

题目

地址：https://leetcode.cn/problems/minimum-size-subarray-sum/

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

思路就是使用滑动窗口来解决

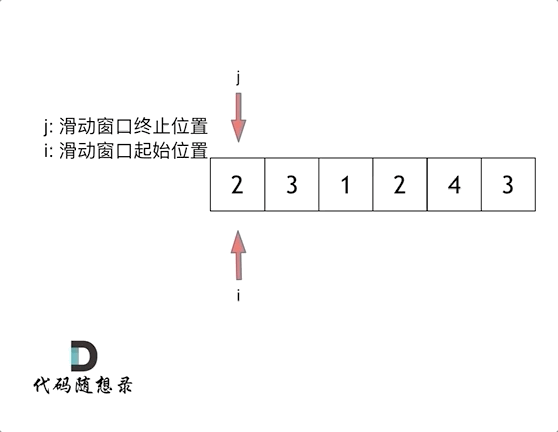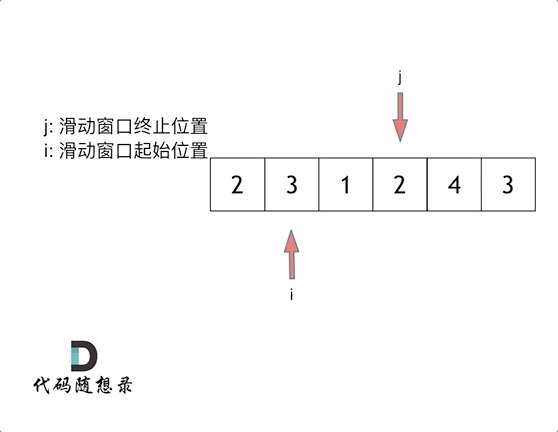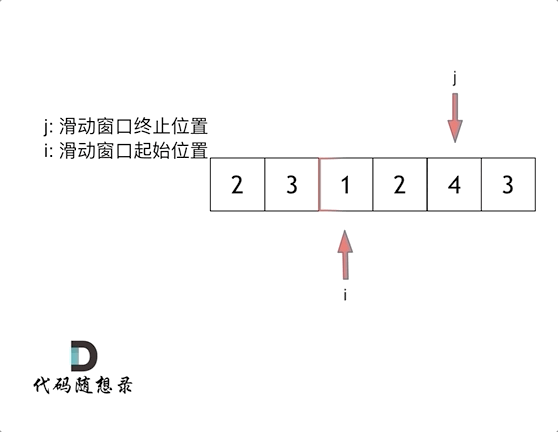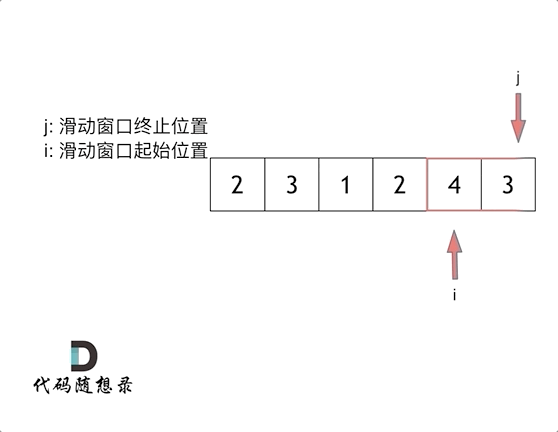
209.长度最小的子数组

代码

class Solution {
     public int minSubArrayLen(int target, int[] nums) {
         int left = 0,sum = 0;//窗口的左边界和总和值
         int result = Integer.MAX_VALUE;
         for(int right=0;right<nums.length;right++){
             sum+=nums[right];
             while(sum>=target){
                 result = Math.min(result,right-left+1);
                 sum = sum - nums[left++];
             }
         }
         return result == Integer.MAX_VALUE ? 0:result;
     }
}

螺旋矩阵II

题目

地址：https://leetcode.cn/problems/spiral-matrix-ii/

给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

示例:

输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]

模拟顺时针画矩阵的过程:

填充上行从左到右
填充右列从上到下
填充下行从右到左
填充左列从下到上

由外向内一圈一圈这么画下去。

这里一圈下来，我们要画每四条边，这四条边怎么画，每画一条边都要坚持一致的左闭右开，或者左开右闭的原则，这样这一圈才能按照统一的规则画下来。

那么我按照左闭右开的原则，来画一圈，大家看一下：

代码

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] nums = new int[n][n];
        int loop = 1;//记录当前的圈数
        int x=0,y=0;//记录起始位置
        int offset = 1;//处理边界情况
        int i,j,count = 1;//行和列
        while(loop <= n/2){
            //从顶部开始螺旋
            for(j=y;j<n-offset;j++){
                nums[x][j] = count++;
            }

            //从右侧开始螺旋
            for(i=x;i<n-offset;i++){
                nums[i][j] = count++;
            }

            //从底部开始螺旋
            for(;j>y;j--){
                nums[i][j] = count++;
            }

            //从左侧开始
            for(;i>x;i--){
                nums[i][j] = count++;
            }
            loop++;
            x++;
            offset++;
            y++;
        }

        if(n % 2 == 1){
            nums[x][y] = count;
        }
        
        return nums;
    }
}

区间和

题目

题目描述

给定一个整数数组 Array，请计算该数组在每个指定区间内元素的总和。

输入描述

第一行输入为整数数组 Array 的长度 n，接下来 n 行，每行一个整数，表示数组的元素。随后的输入为需要计算总和的区间，直至文件结束。

输出描述

输出每个指定区间内元素的总和。

输入案例：

输出案例：

3
9

思路：前缀和在涉及计算区间和的问题时非常有用！

前缀和的思路其实很简单，我给大家举个例子很容易就懂了。

例如，我们要统计 vec[i] 这个数组上的区间和。

我们先做累加，即 p[i] 表示下标 0 到 i 的 vec[i] 累加之和。

如图：

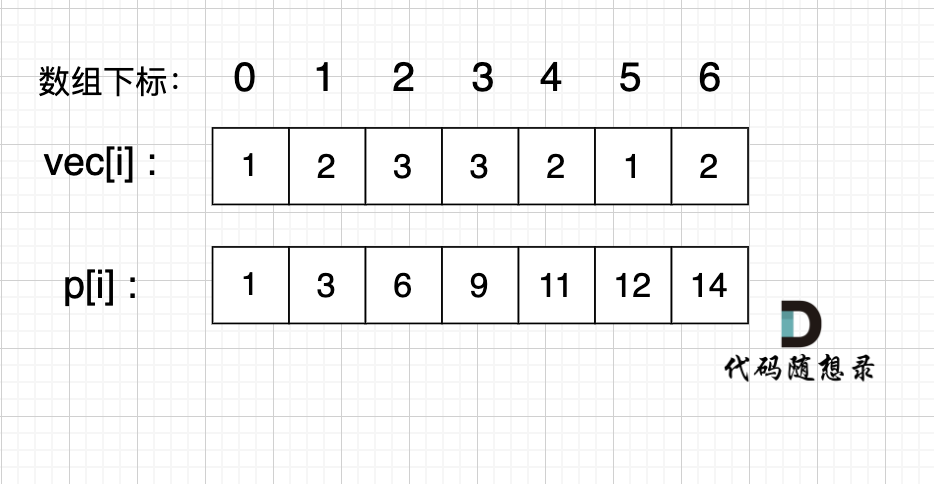
如果，我们想统计，在vec数组上下标 2 到下标 5 之间的累加和，那是不是就用 p[5] - p[1] 就可以了。

为什么呢？

p[1] = vec[0] + vec[1];
p[5] = vec[0] + vec[1] + vec[2] + vec[3] + vec[4] + vec[5];
p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];

这不就是我们要求的下标 2 到下标 5 之间的累加和吗。

如图所示：
在这里插入图片描述

p[5] - p[1] 就是红色部分的区间和。

而 p 数组是我们之前就计算好的累加和，所以后面每次求区间和的之后我们只需要 O(1) 的操作。

特别注意：在使用前缀和求解的时候，要特别注意求解区间。

如上图，如果我们要求区间下标 [2, 5] 的区间和，那么应该是 p[5] - p[1]，而不是 p[5] - p[2]。

代码

import java.util.Scanner;

/**
 * @author: dlwlrma
 * @data 2024年11月29日 19:39
 * @Description 区间和算法
 */
public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int n =sc.nextInt();
        int[] vec = new int[n];
        int[] p = new int[n];

        int presum = 0;
        for (int i = 0; i < n; i++) {
            vec[i] = sc.nextInt();
            presum += vec[i];
            p[i] = presum;
        }

        while(sc.hasNext()){
            int a = sc.nextInt();
            int b = sc.nextInt();

            int sum;
            if(a == 0){
                sum = p[b];
            }else{
                sum = p[b] - p[a-1];
            }
            System.out.println(sum);
        }
        sc.close();
    }
}