本文为学习笔记整理
参考书籍：《深度学习入门 : 基于Python的理论与实现 》/ (日) 斋藤康毅著 ; 陆宇杰译. – 北京 : 人民邮电出版社, 2018.7（2019.5重印）

文章中带编号的图片（如：图4-2）均来自书籍内容。

神经网络的学习

学习：神经网络可以从输入的训练数据中自动获取最优权重参数的过程。

损失函数：学习的指标，以损失函数为基准，找出能使它的值达到最小的权重参数。

从数据中学习

数据是机器学习的核心，机器学习的方法尝试从收集到的数据中发现答案（模式）。

从图像中提取特征量，再用机器学习技术学习这些特征量的模式。

图像的特征量通常表示为向量的形式。在计算机视觉领域，常用的特征量包括 SIFT、SURF和HOG（定向梯度直方图）等。使用这些特征量将图像数据转换为向量，然后对 转换后的向量使用机器学习中的SVM、KNN等分类器进行学习。

图像的特征量的设计需要根据不同的任务来设计专门的特征量，才能得到更好的结果。

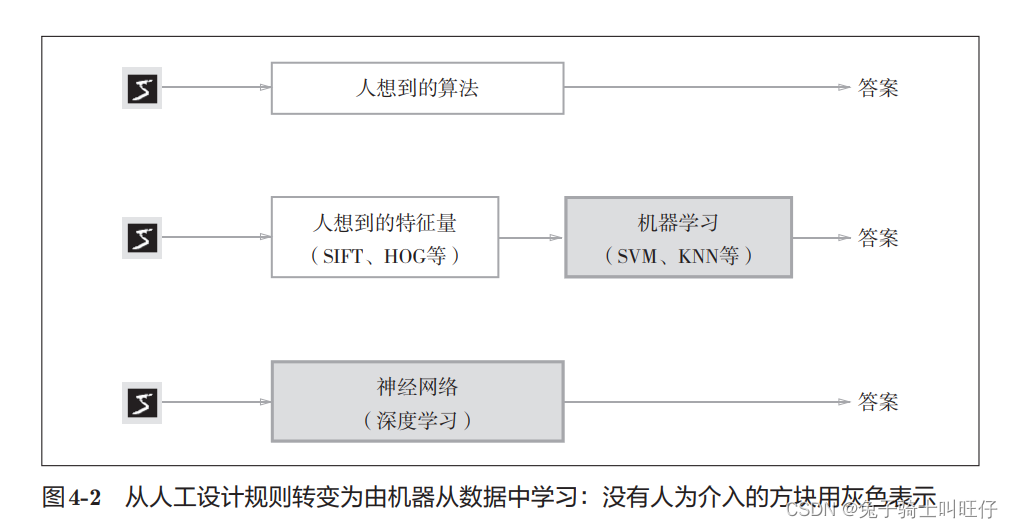
在神经网络中，也就是**深度学习中包含的重要特征量也都是由网络自己学习出来的**

深度学习：端到端机器学习（end-to-end machine learning）。从原始数据中直接获得目标结果。

神经网络对所有的问题都可以用同样的流程来解决，比如识别问题，无论是识别狗还是人脸还是其他，神经网络都是通过提供的数据，从中发现求解问题的模式。

数据区分

数据一般分为：

• 训练数据（监督数据）
  • 使用训练数据寻找最优的参数
• 测试数据
  • 使用测试数据评价训练得到的模型的实际能力

设置训练数据和测试数据是为了正确评价模型的泛化能力，也就是指在处理新的数据时的能力，不能只适用于训练和测试的数据

过拟合：只是对某个数据集过度拟合，就是说训练出来的模型只适用于某个数据集，无法在其他的数据上解决问题。要避免过拟合。

损失函数

损失函数就是一个对学习程度和效果的评价标准

书中定义：

损失函数：神经网络的学习中所用的指标称为损失函数，以这个指标为基准，寻找最优权重参数。损失函数可以使用任意函数，但一般用均方误差和交叉熵误差等。

均方误差

$$E=\frac{1}{2}\sum _k(y_k-t_k{)}^2\text{\hspace{1em}(4.1)}$$

$y_k$：神经网络的输出（实际的输出，如果使用softmax函数输出，就是实际的概率，而不是对应的结果）

$t_k$：监督数据（就是训练数据中的标签）

$k$：数据的维度（每个数据都需要参与运算）

举例：

手写数字识别中的一个输出y：

softmax的输出看作概率，那么推测这个输出对应的输入为“8”

对应的监督数据（实际标签）：

假设推理正确，实际的结果就是“8”，$t$的形状就是：
$$t=[0,0,0,0,0,0,0,0,1,0]$$
数组元素的索引从第一个开始依次对应数字0，1，2，…，9

one-hot表示：正确解标签表示为1，其他标签表示为0

那么对应的均方误差就是上面y和t对应元素相减再平方，然后求和，除以2，得出E。（也就是每一个元素的误差的平方和再除以2）

def mean_squared_error(y, t):
    return 0.5 * np.sum((y - t) ** 2)

交叉熵误差

$$E=-\sum _k{t}_{k}log{y}_k\text{\hspace{1em}(4.2)}$$

其中$log$为以e为底，即$ln$。

$y_k$：神经网络的输出

$t_k$ ：正确解标签，同样是one-hot表示

因此，式（4.2）中，正确解标签对应的输出越大，E的值越接近0，误差越小。比如：

还是手写数字

正确标签：[0, 0, 1, 0, 0, 0, 0, 0, 0, 0]，代表正确解为数字“2”

神经网络输出：[0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]，代表输出的识别结果也是数字"2"

因为0乘任何数都是0，所以最后的交叉熵误差计算就是:$E=-1\ast log0.6=0.5108$

如果神经网络的输出错误，比如是：[0.1, 0.05, 0.1, 0.0, 0.05, 0.6, 0.0, 0.1, 0.0, 0.0]

那么$E=-1\ast log0.1=2.3026$，所以交叉熵误差是基于正确解的一种损失函数的计算方式。

代码实现：

def cross_entropy_error(y, t):
    delta = 1e-7  # 加一个微小值是为了防止np.log(0)的情况，这样会无限大
    return -np.sum(t * np.log(y + delta))

mini-batch学习

机器学习使用训练数据进行学习，就是针对训练数据计算损失函数的值，找出使该值尽可能小的参数。

如果训练数据有100个，就要把这100个损失函数的总和作为学习的指标

那么，此时的交叉熵函数就是：
$$E=-\frac{1}{N}\sum _n\sum _k{t}_{nk}log{y}_{nk}\text{\hspace{1em}(4.3)}$$
$N$：数据个数

$t_{nk}$：第n个数据的第k个元素的值

式子(4.3)只是把求单个数据的损失函数的式子(4.2)扩大到N个数据然后除以N进行正规化（归一化）

通过除以N，可以求单个数据的“平均损失函数”。可以获得和训练数据的数量无关的统一指标。

但是，往往训练数据集的数据量很大，如果以全部数据为对象求损失函数的和，计算过程需要花费较长的时间。因此引出mini-batch学习。

mini-batch学习：从全部数据中选出一批数据（称为mini-batch），然后对每个mini-batch进行学习。

mini-batch的损失函数也是利用一部分样本数据来近似地计算整体。也就是说，用随机选择的小批 量数据（mini-batch）作为全体训练数据的近似值。我理解有点类似抽样调查的意思。

代码实现;

def cross_entropy_error_one_shot(y, t):
    """
    交叉熵误差
    y: 神经网络的输出
    t: 训练数据的标签(监督数据), one-shot表示
    """
    if y.ndim == 1:  # y为一个NumPy矩阵，y.ndim为行数
        # y的维度为1时，即求单个数据的交叉熵误差
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)

    batch_size = y.shape[0]
    # 此时传入的y为一个batch, y.shape[0]为行数，即结果的数量N
    delta = 1e-7  # 加一个微小值是为了防止np.log(0)的情况，这样会无限大
    return -np.sum(t * np.log(y + delta)) / batch_size


def cross_entropy_error_not_one_shot(y, t):
    """
    交叉熵误差
    y: 神经网络的输出
    t: 训练数据的标签(监督数据), 非one-shot表示
    """
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)

    batch_size = y.shape[0]
    delta = 1e-7
    return -np.sum(np.log(y[np.arange(batch_size), t] + delta)) / batch_size

对最后的return结果做一个梳理：

np.arange(batch_size)  # 生成一个从0~(batch_size-1)的数组
y[np.arange(batch_size), t]  
"""
因为t非one-shot表示，所以t就是存储的真正的输出结果，比如[2, 4, 7,...]
y的一行是一个softmax输出的下标0~9的数组,比如[0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
因为交叉熵误差是直接按照正确解来计算
那么这句代码会生成一个NumPY数组：[y[0, 2], y[1, 4], y[2, 7],...,y[batch_size - 1, t对应的结果]]
y[0, 2]: 第一个结果中对应正确解"2"的概率值
y[1, 4]: 第二个结果中对应正确解"4"的概率值
"""

发现个问题：公式(4.3)中有$t_{nk}$和$log{y}_{nk}$的乘积，为什么在$t$使用非one-shot表示时，返回值没有乘积操作呢？

思考：

如果$t$为one-shot表示，那么$t$为0的元素的交叉熵误差也为0，也就是说如果可以获得神经网络在正确解标签处的输出，就可以计算交叉熵误差，此时是输出的正确解标签是乘1，就可以理解为是取$y$在正确解的位置的输出值，所以在$t$为非one-shot表示时，也是要取对应的正确位置的输出值，所以就没有乘积操作了。

损失函数更新的思路

在寻找最优参数（权重和偏置时），为了找到使损失函数的值尽可能小的地方，需要计算参数的导数（也称“梯度”），然后以这个梯度为指引，逐步更新参数的值。

如果导数的值为负数，函数沿梯度方向递减，使该权重参数向正方向（顺梯度方向）改变

如果导数的值为正数，函数沿反梯度方向递减，使该权重参数向反方向改变

当导数的值为0，此时该权重参数的更新会停在此处

在进行神经网络的学习时，不能将识别精度作为指标。因为如果以 识别精度为指标，则参数的导数在绝大多数地方都会变为0。