浮点数的表示—IEEE754标准
引言
我们知道,在计算机中,数字以0和1组成的二进制序列来表示。但是,对于非常大的数字以及非常接近0的数字,简单的存储方式往往会造成精度的丢失。
为了解决这个问题,提供更高效的浮点数表示方法,各大厂商纷纷推出自己的浮点数表示标准。大约在1985年,IEEE(电气和电子工程师协会)推出了754标准,从此,江湖一统。
IEEE754标准浮点格式
IEEE754标准浮点格式由三部分组成: ( − 1 ) S ∗ M ∗ 2 E (-1)^S*M*2^E (−1)S∗M∗2E
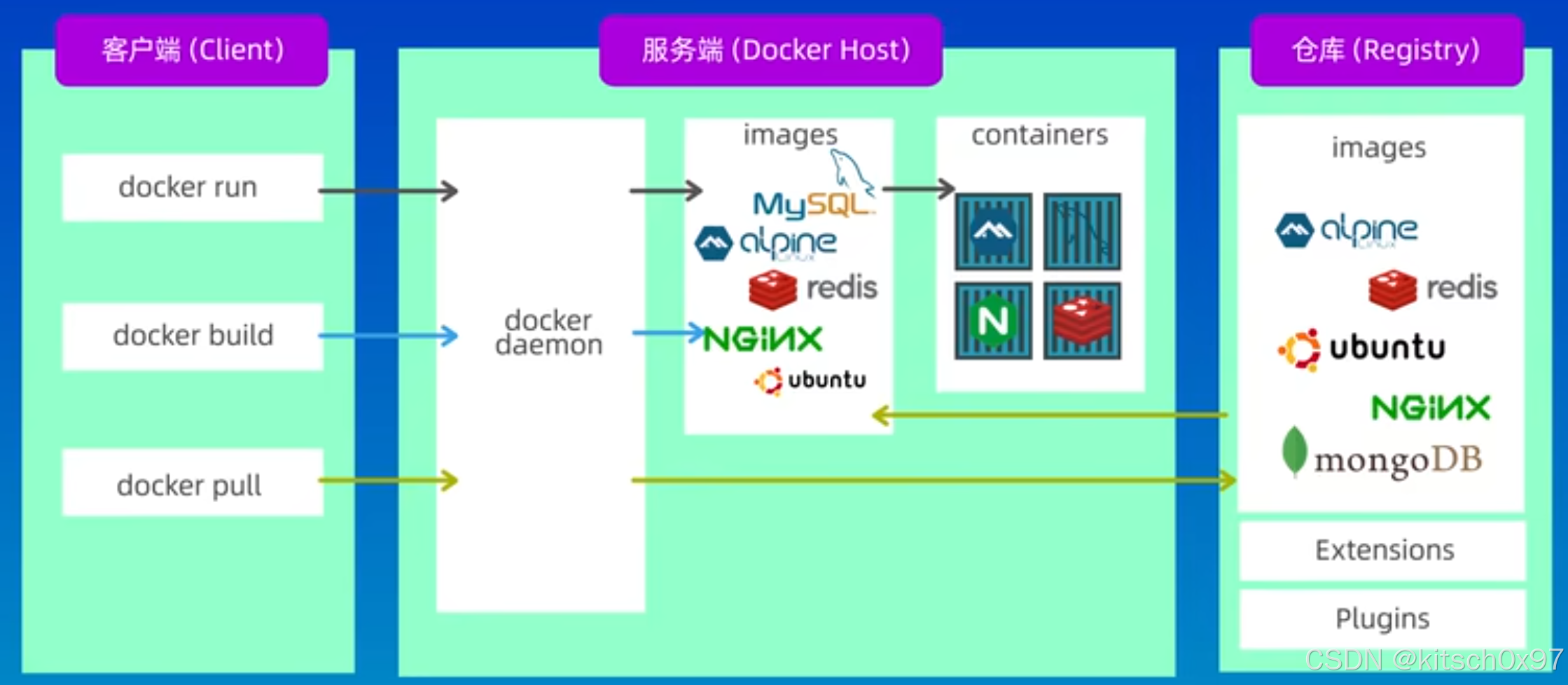
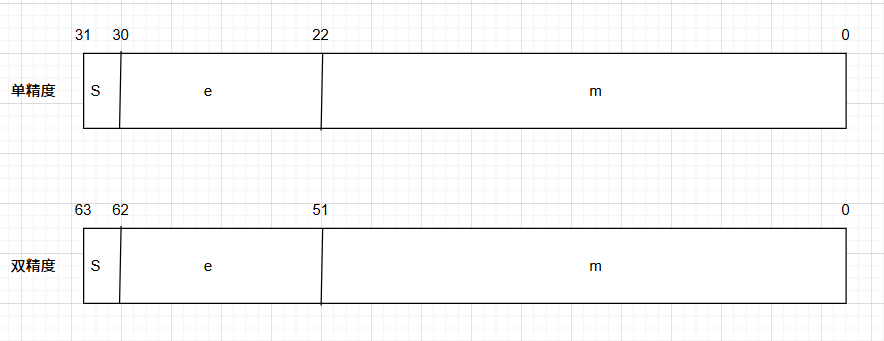
- S:符号,表示浮点数是正数(s=0)还是负数(s=1)
- E:阶码,对浮点数进行加权。阶码被解释为以偏置形式表示的有符号整数,偏置值(Bias)为 2 ( n − 1 ) − 1 2^{(n-1)}-1 2(n−1)−1,n为e所占的位数(Bias单精度为 2 ( 8 − 1 ) − 1 = 12 7 10 = 0111111 1 2 2^{(8-1)}-1=127_{10}=0111 1111_2 2(8−1)−1=12710=011111112,双精度为 2 ( 11 − 1 ) − 1 = 1023 2^{(11-1)}-1=1023 2(11−1)−1=1023)。
- M:尾数,用于表示小数
如下图所示,IEEE754标准浮点格式下的单精度浮点数占32位:符号占1位,阶码占8位,尾数占23位;双精度浮点数占64位。
规格化的值
当阶码位既不全为0也不全为1时,是规格化浮点数。此时E=e-Bias,M>=1。

例子:十进制的 ( − 0.75 ) 10 (-0.75)_{10} (−0.75)10,将其转化为IEEE754格式:
- 转化为二进制: ( − 0.75 ) 10 = ( − 3 / 4 ) 10 = − ( 2 − 1 + 2 − 2 ) 10 = ( − 0.11 ) 2 (-0.75)_{10}=(-3/4)_{10}=-(2^{-1}+2^{-2})_{10}=(-0.11)_2 (−0.75)10=(−3/4)10=−(2−1+2−2)10=(−0.11)2
- 写为 ( − 1 ) S ∗ M ∗ 2 E (-1)^S*M*2^E (−1)S∗M∗2E格式: ( − 1 ) 1 ∗ 1. 1 2 ∗ 2 − 1 2 (-1)^1*1.1_2*2^{-1_2} (−1)1∗1.12∗2−12
- S=1,E=-1,M=1.1, e = E + B i a s = − 1 10 + 12 7 10 = − 0000000 1 2 + 0111111 1 2 = 0111111 0 2 e=E+Bias=-1_{10}+127_{10}=-0000 0001_2 + 0111 1111_2 = 0111 1110_2 e=E+Bias=−110+12710=−000000012+011111112=011111102,将M去除包含的最高位1只留小数部分得到 m = 2 ( − 1 ) 2 = 1000000000000000000000 0 2 m=2^{(-1)_2}=100 0000 0000 0000 0000 0000_2 m=2(−1)2=100000000000000000000002
- 组合S、e、m即得IEEE754格式: 10111111010000000000000000000000 1 011 1111 0100 0000 0000 0000 0000 0000 10111111010000000000000000000000
非规格化的值
当阶码位全为0时,是非规格化浮点数。此时E=1-Bias。

因为M不需要>=1,所以提供了表示非常接近0值的方式。当尾数位也全为0时,表示0。
特殊值
当阶码位全为1时,是特殊浮点数。
此时,如果尾数位也全为1,当阶码位为1时代表负无穷,当阶码位为0时代表正无穷;

当尾数位不全为1时,代表NaN,(Not a Number)不是一个数。
242156)]
当尾数位不全为1时,代表NaN,(Not a Number)不是一个数。