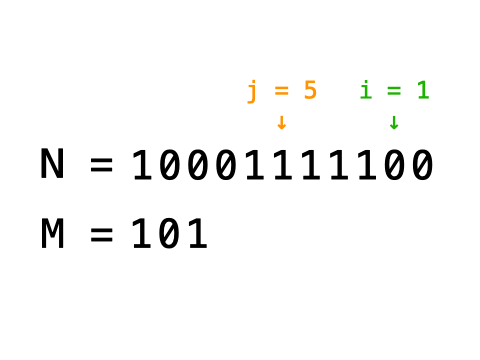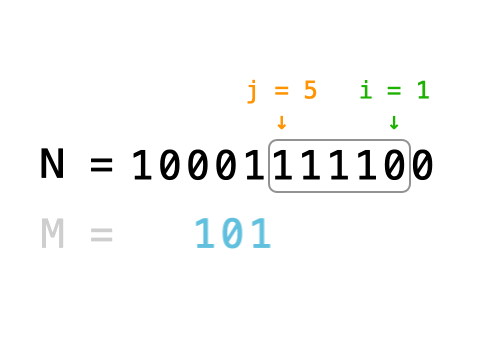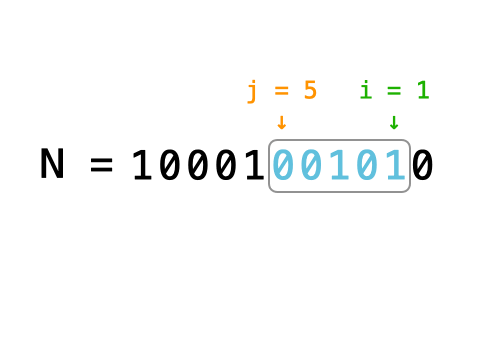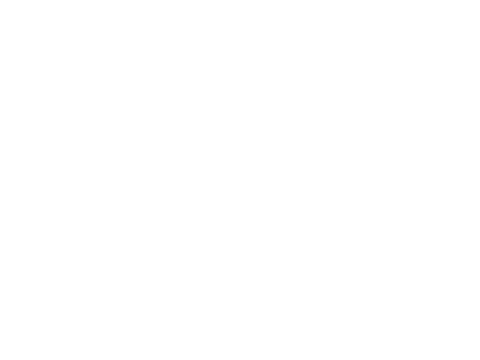T1 扑克牌

link

氺，拿个数组记录下就好。

T2 地图探险

link

氺，小型模拟题。

T3 小木棍

link

题意
用恰好 $n$ 根小木棒拼一个正整数，并且要尽量小。

思路
看一眼数据范围， $n\le 10^5$ ，那拼出来的数很大？要 高精度 ！
然后看到特殊性质，$n$ 是 $7$ 的倍数？数学、贪心、找规律 ！
打个表，然后由于题目告诉我们答案与 $mod$ $7$ 有关，就将同余的数放在一起找规律，规律还是很简单的，注意不重不漏！

#include<bits/stdc++.h>
using namespace std;
int main(){
	int t; cin>>t;
	while(t--){
		int n; cin>>n;
		if(n==1) cout<<"-1\n";
		else if(n==2) cout<<"1\n";
		else if(n==3) cout<<"7\n";
		else if(n==4) cout<<"4\n";
		else if(n==5) cout<<"2\n";
		else if(n==6) cout<<"6\n";
		else if(n==7) cout<<"8\n";
		else if(n%7==0){
			for(int i=1;i<=n/7;i++) cout<<8;
			cout<<"\n";
		}
		else if(n%7==1){
			cout<<10;
			for(int i=1;i<=(n-8)/7;i++) cout<<8;
			cout<<"\n"; 
		}
		else if(n%7==2){
			cout<<1;
			for(int i=1;i<=(n-2)/7;i++) cout<<8;
			cout<<"\n";
		}
		else if(n%7==3){
			if(n==10) cout<<"22\n";
			else{
				cout<<200;
				for(int i=1;i<=(n-17)/7;i++) cout<<8;
				cout<<"\n";
			}
		}
		else if(n%7==4){
			cout<<20;
			for(int i=1;i<=(n-11)/7;i++) cout<<8;
			cout<<"\n";
		}
		else if(n%7==5){
			cout<<2;
			for(int i=1;i<=(n-5)/7;i++) cout<<8;
			cout<<"\n";
		}
		else{
			cout<<6;
			for(int i=1;i<=(n-6)/7;i++) cout<<8;
			cout<<"\n";
		}
	}
	return 0;
}

当然也可以用 $dp$ 做，但是懒得写了。

T4 接龙

link

这题还是很有意思的。

题意
有 $n$ 个人参与接龙游戏，第 $i$ 个人会获得一个整数序列 $S_i$ 作为他的词库。游戏有若干轮，每一轮规则如下：

每一轮由某个人 $p$ 进行接龙（这个人 $p$ 不能与上一轮的人相同，第一轮除外）。

这个人可以取他的词库 $S_p$ 中长度为 $[2,k]$ 的连续一段 $A$ 进行接龙（如果是第一轮，$A$ 需以 $1$ 开头；否则，$A$ 需以上一轮的接龙序列的最后一个元素为开头）。

现在有 $q$ 次询问，第 $i$ 次你需要判断 —— 这 $n$ 个人进行一次游戏，若在第 $r_i$ 轮结束，是否能使最后一次接龙的序列的最后一个元素为 $c_i$ 。

多测，有 $T$ 组数据。

$1\le T\le 5$ , $1\le n\le 10^5$ , $2\le k\le 2\times 10^5$ , $1\le q\le 10^5$

思路
考虑 $DP$ 。
设状态为 $f_{i,j}$ 表示在第 $i$ 轮游戏中，以数字 $j$ 为结尾是否可行。三种情况如下：
$$f_{i,j}=\{\begin{array}{ll}-1& 不可行\\ k& 只有一种可行方案且是由k这个人来完成的\\ 0& 有多种可行方案（即可行方案数>1）\end{array}$$

转移为：（这只是一个大概的）（$A<=B$ ：$A$ 由 $B$ 转移得到）
$$f_{i,j}<=f_{i-1,k}$$

具体的看代码。 时间复杂度为 $O(Tr\sum l)$ 。

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5,maxr=105,maxc=2e5+5;
int f[maxr][maxc];
vector<int>vct[maxn];
int main(){
    ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);
	int T; cin>>T;
	while(T--){
		int n,K,q; cin>>n>>K>>q;
		int manum=0;
		for(int i=1;i<=n;i++){
			int len; cin>>len;
			for(int j=1;j<=len;j++){
				int x; cin>>x;
				vct[i].push_back(x);
				manum=max(manum,x);
			}
		}//f[i][j]：在第 i 轮游戏中，以数字 j 为结尾是否可行（三种情况如下） 
		for(int i=0;i<=100;i++)    
			for(int j=1;j<=manum;j++)
				f[i][j]=-1;//(1) -1：不可行
		f[0][1]=0;
		for(int i=1;i<=100;i++)
			for(int j=1;j<=n;j++){
				int lst=-1;
				for(int k=0;k<vct[j].size();k++){
					if(k>=K&&lst<=k-K) lst=-1;
					int wd=vct[j][k];
					if(lst!=-1){
						if(f[i][wd]==-1) f[i][wd]=j;//(2) j：只有一种可行方案且是由 j 这个人来完成的  
						else if(f[i][wd]!=j) f[i][wd]=0;//(3) 0：有多种可行方案 
					}
					if(f[i-1][wd]!=-1&&f[i-1][wd]!=j) lst=k;//lst：上一个能被转移的数的下标 
				}
			}
		while(q--){
			int r,c; cin>>r>>c;
			cout<<(f[r][c]==-1?0:1)<<"\n";
		}
		for(int i=1;i<=n;i++)
			vct[i].clear();//多测要清空！！！！！！ 
	} 
	return 0;
}