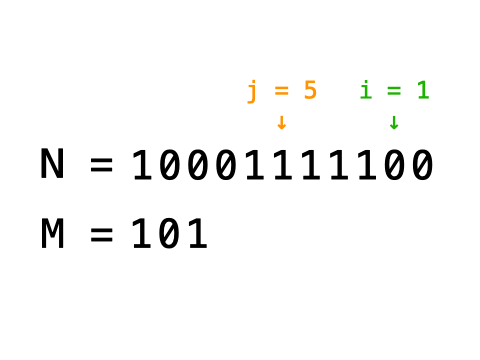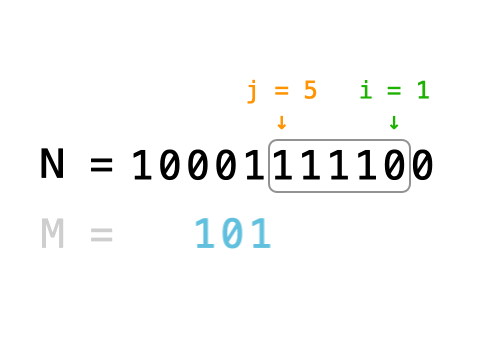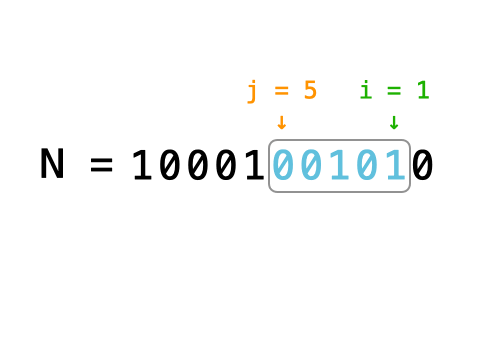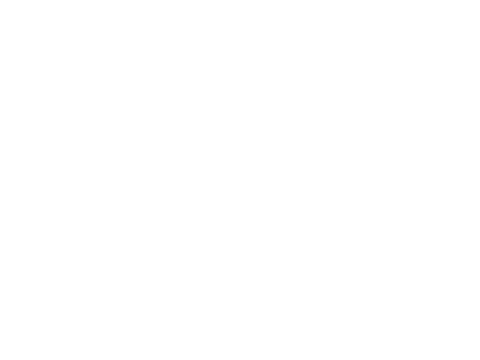一、决策树

1、主要应用场景为分类的问题。采用“树”的理念，通过计算数据的信息熵确定树的根节点、channel，从而加快数据分类。

注：与常规二分类树的区别：决策树中通过依据树的广度与深度，不断确定根节点的root值，同时具有一定的断枝、减枝的功能。

# 手动计算决策树
import pandas as pd
import numpy as np

data = pd.read_excel('shang.xls')
data['age'] = [2 if i >35 else 1 for i in data['age']]
data['money'] = [2 if i >=10000 else 1 for i in data['money']]
data['study'] = [2 if i >= 3 else 1 for i in data['study']]
data = np.array(data)
x = data[:,0:4]
y = data[:,-1]
# 定义信息熵函数
def Log2(x):
    return -x*np.log2(x)

# 计算属性的信息增益
def branch(x,y,m):
    p_work_1 = sum(x[:,m] == 1) / len(x)
    p_work_2 = sum(x[:,m] == 2) / len(x)

    p_work_1_0 = 0
    p_work_1_1 = 0
    p_work_2_0 = 0
    p_work_2_1 = 0

    for i in range(len(y)):
        if x[i,m] == 1:
            if y[i] == 0:
                p_work_1_0 += 1
            else:
                p_work_1_1 += 1
        if x[i,m] == 2:
            if y[i] == 0:
                p_work_2_0 += 1
            else:
                p_work_2_1 += 1

    p_work_1_all = p_work_1_0 + p_work_1_1
    p_work_2_all = p_work_2_0 + p_work_2_1
    
    if p_work_1_0 == 0:
        p_work_1_0 = 0.00001
    else:
        p_work_1_0 /= p_work_1_all

    if p_work_1_1 == 0:
        p_work_1_1 = 0.00001
    else:
        p_work_1_1 /= p_work_1_all

    if p_work_2_0 == 0:
        p_work_2_0 = 0.00001
    else:
        p_work_2_0 /= p_work_2_all

    if p_work_2_1 == 0:
        p_work_2_1 = 0.00001
    else:
        p_work_2_1 /= p_work_2_all
       
    # print("p_work_1_0: ", p_work_1_0)
    # print("p_work_1_1: ", p_work_1_1)
    # print   ("p_work_2_0: ", p_work_2_0)
    # print("p_work_2_1: ", p_work_2_1)

    p_work_H = p_work_1 * (Log2(p_work_1_0) + Log2(p_work_1_1)) + p_work_2 * (Log2(p_work_2_0) + Log2(p_work_2_1))
    return p_work_H

# 返回列表中最大值的下角标
def max_index(list):
    max_index = 0
    for i in range(len(list)):
        if list[i] > list[max_index]:
            max_index = i
    return max_index
# 计算根节点的信息熵
p_0 = sum(y==0)/len(y)
p_1 = sum(y==1)/len(y)
p_H = Log2(p_0)+Log2(p_1)
# print('根节点的信息熵为：',p_H)

all_index = []
n,m = x.shape
for i in range(m):
    p_h = branch(x,y,i)
    p_w = p_H - p_h
    all_index.append(p_w)
    
index = max_index(all_index)
index

# 计算机实现决策树
# 计算过程可视化
# 导入决策树的模块
from sklearn.tree import DecisionTreeClassifier 
desc = DecisionTreeClassifier(criterion="entropy")   # 设定为信息熵方式构建决策树
# 默认criterion="gini"    #  采用基尼指数作为评价标准
from sklearn.datasets import load_iris  
from sklearn.model_selection import train_test_split   
from sklearn.preprocessing import StandardScaler

data = load_iris()
x,y = load_iris(return_X_y=True)

x_train,x_test,y_train,y_test = train_test_split(x,y,train_size=0.75,random_state=1)
satander = StandardScaler()
x_train = satander.fit_transform(x_train)
model = desc.fit(x_train,y_train)
x_test = satander.transform(x_test)
score = model.score(x_test,y_test)
print(score)

2、决策树可视化工具

from sklearn.tree import export_graphviz
export_graphviz(model, out_file="iris_tree.dot", feature_names=data.feature_names)

将产生的model文件，复制到"http://webgraphviz.com/"进行决策树的可视化。

二、随机森林

from sklearn.ensemble import RandomForestClassifier
model =RandomForestClassifier(n_estimators=100,criterion='gini',max_depth=5)

三、线性回归

1、最小二乘法

（1）对方阵进行求导，最终Loss = 1/2||(XW-y)||^2。

# 手动实现方阵的最小二乘法
# 构建参数矩阵
# 最小二乘法计算参数   W=(X^TX)^{-1}X^Ty
# np.linalg.inv()  计算矩阵的逆矩阵
W = np.dot(np.dot(np.linalg.inv(np.dot(x.T,x)),x.T),y)
print(W)

# 手动实现非方阵的最小二乘法
# 构建参数矩阵
# 最小二乘法计算参数   W=(X^TX)^{-1}X^Ty
# np.linalg.inv()  计算矩阵的逆矩阵
W = np.dot(np.dot(np.linalg.pinv(np.dot(x.T,x)),x.T),y)
print(W)

（2）np.linalg.inv()与np.linalg.pinv()的区别

import numpy as np
data = [[1,0],[0,1],[2,2]]
# 采用np.linalg.inv对data进行逆矩阵计算
# 最终结果报错。因为计算矩阵的逆矩阵需方阵
# np.linalg.pinv()的计算机理
data = [[1,0],[0,1],[2,2]]  #data.shape = 3*2
# 将data空缺部分填充极小值，将data填充为方阵
data = [[1,0,0.00001],[0,1,0.00001],[2,2,0.00001]]
# 对data数据进行求逆矩阵 后进行矩阵的减枝 2*3型矩阵
data^-1.shape = 2*3 型矩阵

（3）链式求导计算损失函数

# 链式求导计算矩阵的Loss中W的值  (XW - y) X^T ==> W = X^-1*y*X^T*(X^T^-1)   ==> X^-1*y
# 链式求导 (XW - y) X^T ==> W = X^-1*y
W = np.dot(np.linalg.pinv(x),y)   # 计算非方阵的逆矩阵

（4）线性回归

# 计算机实现最小二乘法
# 没有偏置项
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=False)   
model.fit(x,y)
print(model.coef_)   # 结果与数学公式计算结果一致
print(model.intercept_)

# 计算机实现最小二乘法
# 有偏置项
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)   
model.fit(x,y)
print(model.coef_)   # 结果与数学公式计算结果不一致 
# 需要后续进行讨论
print(model.intercept_)

四、梯度下降

1、单维度梯度下降

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
w = np.linspace(-100, 100, 100)
# 损失函数
def loss_func(w):   
    return (w - 3.5)**2 -4.5*w + 10
plt.plot(w, loss_func(w))
# 损失函数的导数
def d_loss_func(w):
    return 2*(w-3.5)-4.5
# 梯度下降函数
def grid_func(w,learn_speed):
    return w - learn_speed *d_loss_func(w)
    
# np.random.seed(66)
# w= np.random.randint(500)
w = 10
learn_speed = 0.1
# 存储训练过程中的w与loss值
x = [w]
y = [loss_func(w)]
for i in range(100):
    w = grid_func(w,learn_speed)
    x.append(w)
    y.append(loss_func(w))
    # print(loss_func(w))
plt.scatter(x,y)
plt.show()

2、多维度梯度下降

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline

w1 = np.linspace(-100, 100, 100)
w2 = np.linspace(-100, 100, 100)
# 损失函数
def loss_func(w1,w2):
    return (w1 - 3.5)**2 +(w2 - 2)**2+3*w1*w2-4.5*w1+2*w2 + 20
# 损失函数的导数/偏导
def d1_loss_func(w1,w2):
    return 2*(w1-3.5)+3*w2-4.5
def d2_loss_func(w1,w2):
    return 2*(w2-2)+3*w1+2
# 梯度下降函数 
# 多维度、锁定其他的w，每一次对单w进行计算下降。
# 将多维度 转换为 单维度 进行权重的下降
def grid_func(w1,w2,learn_speed):
    w1_old = w1
    w2_old = w2
    w1 = w1_old - learn_speed *d1_loss_func(w1_old,w2_old)
    w2 = w2_old - learn_speed *d2_loss_func(w1_old,w2_old)
    return w1,w2

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(w1,w2, loss_func(w1,w2))

np.random.seed(66)
w1= np.random.randint(50)
w2= np.random.randint(50)
learn_speed = 0.01
# 存储训练过程中的w与loss值
x = [w1]
y = [w2]
z = [loss_func(w1,w2)]
all = []
for i in range(100):
    w1,w2 = grid_func(w1,w2,learn_speed)
    x.append(w1)
    y.append(w2)
    z.append(loss_func(w1,w2))
    dict= {'w1':w1,'w2':w2,'loss':loss_func(w1,w2)}
    all.append(dict)
    # print(f"第{i}步，w1:{w1},w2:{w2},loss:{loss_func(w1,w2)}")

plt.scatter(x,y,z)
plt.show()
# 模型在底部进行动荡
with open('data.txt','w') as f:
    for i in all:
        f.write(str(i)+'\n')
f.close()

3、梯度下降-SGD/M_SGD

from sklearn.linear_model import SGDRegressor
model = SGDRegressor()
# MSGD == 小批量进行梯度下降
from sklearn.linear_model import SGDRegressor
model = SGDRegressor()
batch = 50
n_train = len(data) // batch
for epoch in range(model.max_iter):
	for i in range(n_train):
		# 对train数据集进行手动切分
		start_index = i * batch
		stop_index = (i+1) * batch
		x_train = data[start_index,stop_index]
		y_train = data[start_index,stop_index]
		# 对模型进行训练  partial_fit 每次fit不会抵消之前fit好的weight
		model.partial_fit(x_train,y_train)
# 得到模型
model.coef_  # 获得模型中最后的参数
model.intercept_  # 获得b

4、正则化

## 核心思想 == 抑制W的发展