形态学图像处理(Morphological Image Processing)

前言

‍

本博客为个人总结数字图像处理一课所写，并给出适当的扩展和相应的demo。

写博客跟做 checkpoint 很像，毕竟个人还不能达到那种信手拈来的境界，忘了就是从零开始训练，这就令人有些头疼了。

题外话说完，开始吧。

‍

Note:

‍

笔者环境为 Ubuntu 24.04 LTS
延续以往的写作风格，我会用自己的话来理解，而非简单直接地贴上原本的概念(目的不是写paper)，那当然是尽量侧重通俗易懂了，除非我才疏学浅，没词了
令人感到悲哀的是，我所谓的数字图像处理课的教材没这玩意(~~反正我也基本不用~~)，我得参考一些资料，尤其是英文的资料。

‍

形态学图像处理(Morphological Image Processing)
- 前言
- 目录
- 什么叫形态学图像处理(Morphological Image Processing)
- 集合论须知的公式
- 结构元素(structuring element)
- - 简要介绍
  - 邻域“窗口”算子(Neighborhood "window" operator)与结构元素
  - 结构元素的三大属性的影响
- 简述算子是什么
- 二值形态学的基本运算
- - 腐蚀(Erosion)
  - - 腐蚀的解释与公式
    - 腐蚀的应用
    - 腐蚀操作的demo实现
  - 膨胀(Dilation)
  - - 膨胀的解释与公式
    - 膨胀的应用
    - 膨胀操作的demo实现
  - 膨胀与腐蚀的关系
  - 开运算(Opening)
  - - 开运算的简介
    - 开运算的demo实现
  - 闭运算(Closing)
  - - 闭运算的简介
    - 闭运算的demo实现
  - 开闭运算的侧重
  - 顶帽运算(Top Hat)
  - - 顶帽运算的简介
    - 顶帽运算的demo实现
  - 黑帽运算(Black Hat)
  - - 黑帽运算的简介
    - 黑帽运算的demo实现
  - 梯度运算(Gradient)
  - - 梯度运算的简介
    - 梯度运算的demo实现
  - 击中击不中变换(Hit - miss filter)
  - - 击中击不中变换的解释与公式
    - 击中击不中变换的应用
- 灰度形态学的基本运算
- - 灰度图像
  - Flat/一般腐蚀算子
  - Flat/一般膨胀算子
  - Flat腐蚀和膨胀算子和一般腐蚀和膨胀算子
- 形态学边缘检测(Morphological edge detectors)
- - 简要介绍
  - 对于二值图像
  - 对于灰度图像
- 参考资料
- - data
  - blog and related sources

‍

什么叫形态学图像处理(Morphological Image Processing)

‍

什么是形态学图像处理呢？

我们打一个比方，我们讲皮肉骨，图像的形态就好比是皮肉，支撑起皮肉的是骨头，我们的形态学处理就是做生物改造，通过改变里面的骨头，进而改变其外在的皮肉的表现。

怎么改变骨头呢？换骨头，按照定好的规则对于原本的骨头用定制的骨头进行替换。

简而言之，就是侧重于图像”皮肉“下的”骨头“的处理。

‍

下面是正式一点的介绍：

‍

形态学图像处理在图像分析中具有重要地位，广泛应用于计算机视觉、图像分割、特征提取等领域。

其主要操作包括膨胀、腐蚀、开闭运算、边缘检测等，这些操作基于集合理论，通过定义结构元素对图像进行处理，能够有效提取图像的形状、结构和特征信息，为后续的分析和理解奠定基础。

‍

集合论须知的公式

‍

概念，如无必要，就直接上公式

‍

集合的并(Union):

$\cup B = \{x \mid x \in A \text{ or } x \in B\}$

集合的交(Intersection):

$\cap B = \{x \mid x \in A \text{ and } x \in B\}$

集合的补(Complement)：

$\overline{A} = \{x \mid x \notin A\}$

集合的差(Difference):

$\{x \mid x \in A \text{ and } x \notin B\}$

集合的反射(Reflection):

$A^{'} = \{(-x, -y) \mid (x, y) \in A \}$

集合的平移(Translation):

$\mathbf{y} = \{ (x + y_1, y + y_2) \mid (x, y) \in A \}$

‍

结构元素(structuring element)

‍

简要介绍

‍

提到图像形态学处理，我们绕不开的一个概念是结构元素，所谓的结构元素(也称核或模板)是一个小的二值(binary)图像，用于与输入图像进行数学操作，以提取图像的特定形状特征。

什么是二值图像呢？就是一个尺寸较小 $\{3\times3,5\times5,\ldots\}$ 的图像(或者叫方阵)，只包含0(背景，黑色)，1(前景，白色)两种像素值。它是灰度/彩色图像分析系统中的中间抽象，常用于阈值分割、判断图像属性等，如文本和线条图形、文档图像处理。

结构元素有多种形状，常见的为方形，圆形，十字形，线形等等。

确定了结构元素的大小和形状后，我们还需要确定结构元素中的原点(锚点)，所谓原点，就是结构元素中用于与输入图像对齐的参考点，具体描述就是，结构元素跟原图像某个位置按运算的规则匹配上后，就会基于锚点和运算进行相应的像素值的处理。

综上，结构元素有三大属性，大小，形状，原点。

‍

邻域“窗口”算子(Neighborhood “window” operator)与结构元素

‍

邻域“窗口”算子，同结构元素密切相关，其公式表示为：

$W\{f[x, y]\}=\left\{f\left[x-x', y-y'\right]:\left[x', y'\right] \in \prod_{x y}\right\}$

这里， $f [x, y]$ 是图像在坐标 $(x, y)$ 处的像素值， $\Pi_{xy}$ 定义了一个特定的邻域范围，它确定了在处理像素 $f [x, y]$ 时，需要考虑的周围像素的集合范围。

它与结构元素的不同在于，它是用结构元素去选取图像中的像素集合，再根据具体的形态学操作对这些像素值进行组合计算，而结构元素本身并不进行计算操作，个人以为，这也是为什么结构元素又被叫做模板的原因。

说的通俗点，拿印章举例，结构元素就是印章的图案，邻域“窗口”算子则是印章的印油。

这个公式也有两个变种，这两个变种，我们会在后面的二值形态学的基本运算中用到。

$W^{\left(-\right)}\{f[x,y]\}=\left\{f\left[x-x^{\prime},y-y^{\prime}\right]:\left[x^{\prime},y^{\prime}\right]\in\prod_{xy}\right\}$

‍

根据结构元素 $\Pi_{xy}$ 的形状和大小，确定图像 $f$ 中以 $(x, y)$ 为中心的邻域->
对于结构元素 $\Pi_{xy}$ 中的每一个点 $(x^{'}, y^{'})$ 计算图像 $f$ 中对应的点 $(x - x^{'}, y - y^{'})$ ->
获取该点的像素值 $f [x - x^{'}, y - y^{'}]$ ->
将所有这些像素值收集到一个集合中，这个集合就是 $W^{(-)}\{f[x,y]\}$ 。

$W^{\left(+\right)}\{f[x,y]\}=\left\{f\left[x+x^{\prime},y+y^{\prime}\right]:\left[x^{\prime},y^{\prime}\right]\in\prod_{xy}\right\}$

同理。

‍

结构元素的三大属性的影响

‍

前面我们提到，结构元素有三大属性，那么这三大属性会怎样影响最后的处理效果呢？

大小，越大说明什么，变化大，影响的范围大，形态学的操作效果会更明显，对原本图像的“骨架”进行更大影响，相应的细节就可能在处理中发生丢失，小的话，则相反。

形状，不同的形状，意味着处理的侧重不同，结构元素的形状，决定了改造后的图像的“骨架”的倾向。

原点，可以理解为我们的工作中心，中心在哪里，处理的结果的落脚点就在在哪里。原点的不同使得最终“骨架”的变化方向，细节处理和特征的匹配有显著的影响。

‍

简述算子是什么

‍

我想，很多同我一样的初学者会有一个疑问，什么是算子？

我们知道函数，简单来说，函数的构成是输入，特定的规则，和将输入经过规则变换得到的结果。

算子的构成则是输入的函数，特定的规则，和将输入的函数经过规则变换得到的另一个函数的映射或操作规则。

换而言之，算子处理的对象，是函数。

‍

二值形态学的基本运算

‍

二值形态学的基本运算包括腐蚀、膨胀、开运算和闭运算。这些运算在图像处理中用于提取图像的形状特征，如边界、区域和连通性等。

二值图像中像素用 $0$ (背景，黑色)和 $1$ (前景，白色)表示，是灰度/彩色图像分析系统中的中间抽象。

有一点值得注意，各种形态学的运算操作，都是基于腐蚀和膨胀操作的组合。

因此，我们可以说，在二值形态学下和灰度形态学下的形态学运算，我们只需要专门关注腐蚀和膨胀操作的不同即可，其余的组合运算就不需要反复强调。

‍

腐蚀(Erosion)

‍

腐蚀的解释与公式

‍

首先我们得回答一个问题，为什么叫腐蚀？

字面意思来讲，就是将一个东西进行“消减”的操作，那么首先想到的效果就是，“变细”或者“变瘦”。在我们的二值图像中的表现，就是将前景物体(像素值为 $1$ )缩小。

把公式先端上来：

$g[x,y]=AND[W^{(+)}\{f[x,y]\}]:=erode(f,W)$

其含义为对于每个像素 $f [x, y]$ ， $W^{(+)}$ 按照 $\Pi_{xy}$ 定义的邻域范围移动结构元素，选取结构元素覆盖到的像素值进行逻辑与 $A N D$ 操作。

当结构元素 $W^{(+)}$ 在图像上移动时，只有当结构元素覆盖区域内的所有像素值都为 $1$ 时，在腐蚀后的图像 $g [x, y]$ 中，对应结构元素中心位置的像素值才为 $1$ ；只要该区域内有一个像素值为 $0$ ，那么腐蚀后对应位置的像素值就为 $0$ 。

我想，得画图才能表示地更加清晰。

‍

QQ20241113-142008

‍

通过上图，再直观一点说，腐蚀操作是用结构元素扫描图像中的每一个像素，当结构元素与图像中对应区域完全匹配时，结构元素中心所对应的像素在腐蚀后的图像中才被置为 $1$ ，否则被置为 $0$ 。

对于上面的公式，我们可能比较陌生，我们更熟悉的可能是下面这个公式：

$\ominus B = \{ x \mid (B)_{y} \subseteq A \}$

其中：

‍

$A$ ：表示原始的二值图像，其中包含前景(值为1的像素)和背景(值为0的像素)。
$B$ ：表示结构元素，它是一个较小的二值图像，用于探测 $A$ 中的特定形状或特征。
$\ominus$ ：表示腐蚀操作。
$B)_{y}$ ：表示结构元素 $B$ 通过平移操作，使其原点移动到空间中的位置 $y$ 。

‍

简单地解释这个公式：若 $B)_{y}$ 仍包含于 $A$ 中，则其所有 $y$ 点组成的集合，称为 $A$ 被 $B$ 腐蚀。

‍

腐蚀的应用

‍

去除噪声：去除孤立噪声点
图像细化：得到骨架结构
目标分离：分离粘连目标
特征提取：获取边界信息

‍

腐蚀操作的demo实现

‍

import cv2
import numpy as np
from matplotlib import pyplot as plt

def save_pair_imgs(imgs,original_title,processed_title):
    plt.figure(figsize=(10, 8))

    plt.subplot(1, 2, 1)
    plt.imshow(imgs[0],'gray')
    plt.title(original_title)
    plt.xticks([]), plt.yticks([])

    plt.subplot(1, 2, 2)
    plt.imshow(imgs[1],'gray')
    plt.title(processed_title)
    plt.xticks([]), plt.yticks([])

    title = original_title + '_' + processed_title

    plt.savefig(f'../imgs/{title}.png', bbox_inches='tight')
    plt.show()

# 读取图像
image = cv2.imread('../data/Lena.bmp', 0)  # 0表示以灰度模式读取

# 定义结构元素
kernel = np.ones((5,5), np.uint8)

# 腐蚀操作
erosion = cv2.erode(image, kernel, iterations = 1)
save_pair_imgs([image,erosion],'Original Image','Erosion')

‍

效果图如下：

‍

Original Image_Erosion

‍

膨胀(Dilation)

‍

膨胀的解释与公式

‍

膨胀，跟腐蚀相反，它是把图像进行一个“变胖”或者说“变粗”的操作。二值图像中的表现，就是将前景物体扩大。

端上公式：

$g[x,y]=OR[W^{(-)}\{f[x,y]\}]:=dilate(f,W)$

当结构元素 $W^{(-)}$ 在图像上移动时，只有当结构元素覆盖区域内的所有像素值都为 $0$ 时，在膨胀后的图像 $g [x, y]$ 中，对应结构元素中心位置的像素值才为 $0$ ；只要该区域内有一个像素值为 $1$ ，那么膨胀后对应位置的像素值就为 $1$ 。

继续上图：

‍

QQ20241113-171552

‍

直观一点说，膨胀操作是用结构元素扫描图像中的每一个像素，当结构元素与图像中对应区域至少有一个匹配时，结构元素中心所对应的像素在膨胀后的图像中就被置为 $1$ ，否则被置为 $0$ 。

同样地，我们通常看到的是下面的公式：

$\oplus B = \{ x \mid (B)_{y}\cap A \neq \emptyset \}$

其中：

‍

$A$ ：表示原始的二值图像，其中包含前景(值为1的像素)和背景(值为0的像素)。
$B$ ：表示结构元素，它是一个较小的二值图像，用于探测 $A$ 中的特定形状或特征。
$\oplus$ ：表示膨胀操作。
$B)_{y}$ ：表示结构元素 $B$ 通过平移操作，使其原点移动到空间中的位置 $y$ 。

‍

简单地解释这个公式：若 $B)_{y}$ 与 $A$ 的交集不为空，则其所有 $y$ 点组成的集合，称为 $A$ 被 $B$ 膨胀。

‍

膨胀的应用

‍

图像预处理：填充孔洞，连接断裂部分
目标增强：突出物体轮廓，扩大目标区域
形态学梯度计算：获取边缘信息

‍

膨胀操作的demo实现

‍

import cv2
import numpy as np
from matplotlib import pyplot as plt

def save_pair_imgs(imgs,original_title,processed_title):
    plt.figure(figsize=(10, 8))

    plt.subplot(1, 2, 1)
    plt.imshow(imgs[0],'gray')
    plt.title(original_title)
    plt.xticks([]), plt.yticks([])

    plt.subplot(1, 2, 2)
    plt.imshow(imgs[1],'gray')
    plt.title(processed_title)
    plt.xticks([]), plt.yticks([])

    title = original_title + '_' + processed_title

    plt.savefig(f'../imgs/{title}.png', bbox_inches='tight')
    plt.show()

# 读取图像
image = cv2.imread('../data/Lena.bmp', 0)  # 0表示以灰度模式读取

# 定义结构元素
kernel = np.ones((5,5), np.uint8)

# 膨胀操作
dilation = cv2.dilate(image, kernel, iterations=1)
save_pair_imgs([image, dilation], 'Original Image', 'Dilation')

‍

效果图如下：

‍

Original Image_Dilation

‍

膨胀与腐蚀的关系

‍

对偶性

$d i l a t e (f, W) = NOT [ero d e (NOT [f], W)]$

$ero d e (f, W) = NOT [d i l a t e (NOT [f], W)]$

也就是说，对前景进行膨胀，相当于对背景进行腐蚀，对背景进行腐蚀，相当于对前景进行膨胀。
但腐蚀不是膨胀的逆运算

$f[x,y]\neq erode(dilate(f,W),W)\neq dilate(erode(f,W),W)$

‍

开运算(Opening)

‍

开运算的简介

‍

开运算是先腐蚀后膨胀的组合操作:

$o p e n (f, W) = d i l a t e (ero d e (f, W), W)$

‍

我们更常见的公式如下:

$\circ B = (A \ominus B) \oplus B$

其中， $A$ 是原始图像， $B$ 是结构元素。

前面我们知道，腐蚀可以去除皮肉，露出"骨架"，去掉噪声的同时会损失一些细节，那么我们就用膨胀操作，把它们长回来，那不就可以做到去掉噪声，又基本保留物体原本的轮廓了吗(腐蚀和膨胀没有逆运算的性质，所以说是基本)?

简单来说，开运算所做的就是去除小的前景部分(数值为1)，也就是去除一些细小突出物、较小的粘连、小面积的噪声，同时保持了物体的基本形状。

‍

开运算的demo实现

‍

import cv2
import numpy as np
from matplotlib import pyplot as plt

def save_pair_imgs(imgs,original_title,processed_title):
    plt.figure(figsize=(10, 8))

    plt.subplot(1, 2, 1)
    plt.imshow(imgs[0],'gray')
    plt.title(original_title)
    plt.xticks([]), plt.yticks([])

    plt.subplot(1, 2, 2)
    plt.imshow(imgs[1],'gray')
    plt.title(processed_title)
    plt.xticks([]), plt.yticks([])

    title = original_title + '_' + processed_title

    plt.savefig(f'../imgs/{title}.png', bbox_inches='tight')
    plt.show()

# 读取图像
image = cv2.imread('../data/Lena.bmp', 0)  # 0表示以灰度模式读取

# 定义结构元素
kernel = np.ones((5,5), np.uint8)

# 开运算操作
opening = cv2.morphologyEx(image, cv2.MORPH_OPEN, kernel)
save_pair_imgs([image, opening], 'Original Image', 'Opening')

‍

效果图如下：

‍

Original Image_Opening

‍

闭运算(Closing)

‍

闭运算的简介

‍

闭运算是先膨胀后腐蚀的组合操作:

$c l ose (f, W) = ero d e (d i l a t e (f, W), W)$

我们更常见的公式如下:

$\bullet B = (A \oplus B) \ominus B$

其中， $A$ 是原始图像， $B$ 是结构元素。

我们为什么要闭运算？先膨胀，去除边界凹陷，包含掉背景噪声，填充孔洞，连接相邻，再腐蚀，就能将包含的背景噪声去除，也保留物体原本的主要特征。

闭运算去除的是小的背景部分(数值为0)。

‍

闭运算的demo实现

‍

import cv2
import numpy as np
from matplotlib import pyplot as plt

def save_pair_imgs(imgs,original_title,processed_title):
    plt.figure(figsize=(10, 8))

    plt.subplot(1, 2, 1)
    plt.imshow(imgs[0],'gray')
    plt.title(original_title)
    plt.xticks([]), plt.yticks([])

    plt.subplot(1, 2, 2)
    plt.imshow(imgs[1],'gray')
    plt.title(processed_title)
    plt.xticks([]), plt.yticks([])

    title = original_title + '_' + processed_title

    plt.savefig(f'../imgs/{title}.png', bbox_inches='tight')
    plt.show()

# 读取图像
image = cv2.imread('../data/Lena.bmp', 0)  # 0表示以灰度模式读取

# 定义结构元素
kernel = np.ones((5,5), np.uint8)

# 闭运算操作
closing = cv2.morphologyEx(image, cv2.MORPH_CLOSE, kernel)
save_pair_imgs([image, closing], 'Original Image', 'Closing')

‍

效果图如下：

‍

Original Image_Closing

‍

开闭运算的侧重

‍

闭运算的侧重点，是去除小的背景部分，保留主要**特征**。

开运算的侧重点，是去除小的前景部分，保留主要**轮廓**。

‍

顶帽运算(Top Hat)

‍

顶帽运算的简介

‍

顶帽运算也称为礼帽运算，它是原图像与开运算结果的差值。

其公式定义如下：

$\circ b)$

‍

顶帽运算能够提取出图像中比周围结构元素尺寸范围内背景更亮的部分，它主要用于分离图像中的明亮部分（如比周围区域亮的物体或噪声）与整体背景。

也就是，分离出噪声信息或者比元素图像更亮的边缘信息。

‍

顶帽运算的demo实现

‍

import cv2
import numpy as np
from matplotlib import pyplot as plt

def save_pair_imgs(imgs,original_title,processed_title):
    plt.figure(figsize=(10, 8))

    plt.subplot(1, 2, 1)
    plt.imshow(imgs[0],'gray')
    plt.title(original_title)
    plt.xticks([]), plt.yticks([])

    plt.subplot(1, 2, 2)
    plt.imshow(imgs[1],'gray')
    plt.title(processed_title)
    plt.xticks([]), plt.yticks([])

    title = original_title + '_' + processed_title

    plt.savefig(f'../imgs/{title}.png', bbox_inches='tight')
    plt.show()

# 读取图像
image = cv2.imread('../data/Lena.bmp', 0)  # 0表示以灰度模式读取

# 定义结构元素
kernel = np.ones((5,5), np.uint8)

# Top Hat 操作
tophat = cv2.morphologyEx(image, cv2.MORPH_TOPHAT, kernel)
save_pair_imgs([image, tophat], 'Original Image', 'Top Hat')

‍

效果图如下：

‍

Original Image_Top Hat

‍

黑帽运算(Black Hat)

‍

黑帽运算的简介

‍

黑帽运算的功能与顶帽运算相反，它能够提取出图像中比周围结构元素尺寸范围内背景更暗的部分，主要用于分离图像中的暗部分（如比周围区域暗的物体或阴影）与整体背景。

也就是，获取图像内部的小孔，前景色中的小黑点，或者比原始图像的边缘更暗的边缘部分。

黑帽运算是闭运算结果与原图像的差值。

其公式定义如下：

$\cdot b) - f$

‍

黑帽运算的demo实现

‍

import cv2
import numpy as np
from matplotlib import pyplot as plt

def save_pair_imgs(imgs,original_title,processed_title):
    plt.figure(figsize=(10, 8))

    plt.subplot(1, 2, 1)
    plt.imshow(imgs[0],'gray')
    plt.title(original_title)
    plt.xticks([]), plt.yticks([])

    plt.subplot(1, 2, 2)
    plt.imshow(imgs[1],'gray')
    plt.title(processed_title)
    plt.xticks([]), plt.yticks([])

    title = original_title + '_' + processed_title

    plt.savefig(f'../imgs/{title}.png', bbox_inches='tight')
    plt.show()

# 读取图像
image = cv2.imread('../data/Lena.bmp', 0)  # 0表示以灰度模式读取

# 定义结构元素
kernel = np.ones((5,5), np.uint8)

# Black Hat 操作
blackhat = cv2.morphologyEx(image, cv2.MORPH_BLACKHAT, kernel)
save_pair_imgs([image, blackhat], 'Original Image', 'Black Hat')

‍

效果图如下：

‍

Original Image_Black Hat

‍

梯度运算(Gradient)

‍

梯度运算的简介

‍

什么是梯度运算，梯度，我们下意识可以想到高数中的梯度。

梯度是一个向量，其方向指向标量函数增长最快的方向，其大小（或长度）表示该方向上的增长速率。

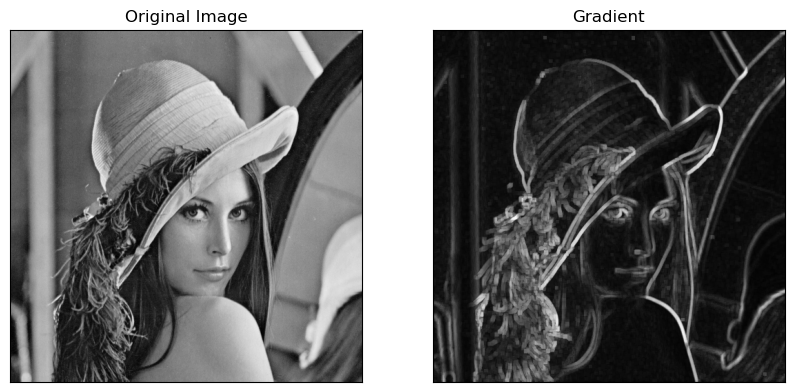
边缘通常是图像中物体与背景之间像素值变化剧烈的地方，因此，梯度运算可以突出图像中的边缘信息(位置和强度)

梯度运算的公式很多，常见的基本差分梯度公式如下：

‍

对于二维离散图像 $f (x, y)$
- 水平方向梯度： $G_x = f(x + 1,y) - f(x,y)$ ，它衡量了图像在水平方向上相邻像素值的变化。例如，在一个灰度图像中，如果从左到右像素值逐渐增加，那么 $G_x$ 在相应位置将为正值，表示从暗到亮的变化趋势；反之，如果像素值逐渐减小， $G_x$ 为负值，表示从亮到暗的变化。
- 垂直方向梯度： $G_y = f(x,y + 1) - f(x,y)$ ，用于检测图像在垂直方向上的像素值变化情况。与 $G_x$ 类似，其正负值反映了垂直方向上像素值的增减趋势。
- 总的梯度幅值 $\sqrt{G_x^2 + G_y^2}$ ，这种计算方式综合考虑了水平和垂直方向的梯度变化，得到一个标量值，表示每个像素点的梯度大小。梯度值越大，说明该像素点处图像的变化越剧烈，越有可能是边缘位置。

‍

梯度运算的demo实现

‍

import cv2
import numpy as np
from matplotlib import pyplot as plt

def save_pair_imgs(imgs,original_title,processed_title):
    plt.figure(figsize=(10, 8))

    plt.subplot(1, 2, 1)
    plt.imshow(imgs[0],'gray')
    plt.title(original_title)
    plt.xticks([]), plt.yticks([])

    plt.subplot(1, 2, 2)
    plt.imshow(imgs[1],'gray')
    plt.title(processed_title)
    plt.xticks([]), plt.yticks([])

    title = original_title + '_' + processed_title

    plt.savefig(f'../imgs/{title}.png', bbox_inches='tight')
    plt.show()

# 读取图像
image = cv2.imread('../data/Lena.bmp', 0)  # 0表示以灰度模式读取

# 定义结构元素
kernel = np.ones((5,5), np.uint8)

# 梯度操作
gradient = cv2.morphologyEx(image, cv2.MORPH_GRADIENT, kernel)
save_pair_imgs([image, gradient], 'Original Image', 'Gradient')

‍

效果图如下：

‍

Original Image_Gradient

‍

击中击不中变换(Hit - miss filter)

‍

击中击不中变换的解释与公式

‍

击中击不中变换用于在二值图像中检测特定形状和结构，它基于结构元素与图像像素的匹配情况来确定目标形状或结构的位置。

击中击不中变换需要使用两个结构元素：结构元素 $V$ （用于匹配前景，目标元素）和结构元素 $W$ （用于匹配背景，目标元素的周围的背景元素）。对于图像中的每个像素点，当以该像素点为中心的图像区域与结构元素 $V$ 在前景部分完全匹配，同时与结构元素 $W$ 在背景部分完全匹配时，该像素点被标记为目标形状或结构的位置。

设二值图像为 $f$ ，击中击不中变换后的图像为 $g$ ，则击中击不中变换可以表示为：

$\circledast (V,W)$

其中 $\circledast$ 表示击中击不中变换操作。

具体计算时，先对图像 $f$ 进行腐蚀操作，腐蚀结构元素为 $V$ ，得到一个中间结果 $f_V$ ；

再对图像 $f$ 的补集（即背景部分）进行腐蚀操作，腐蚀结构元素为 $W$ ，得到另一个中间结果 $f_W^C$ ；最后将 $f_V$ 和 $f_W^C$ 进行逻辑与操作，得到击中击不中变换的结果 $g$ ，即：

$\ominus V) \cap (f^C \ominus W)$

其中 $\ominus$ 表示腐蚀操作， $f^C$ 表示 $f$ 的补集。

我们可以理解为完全匹配，前景和背景元素需要跟设定的完全一致。

上图：

‍

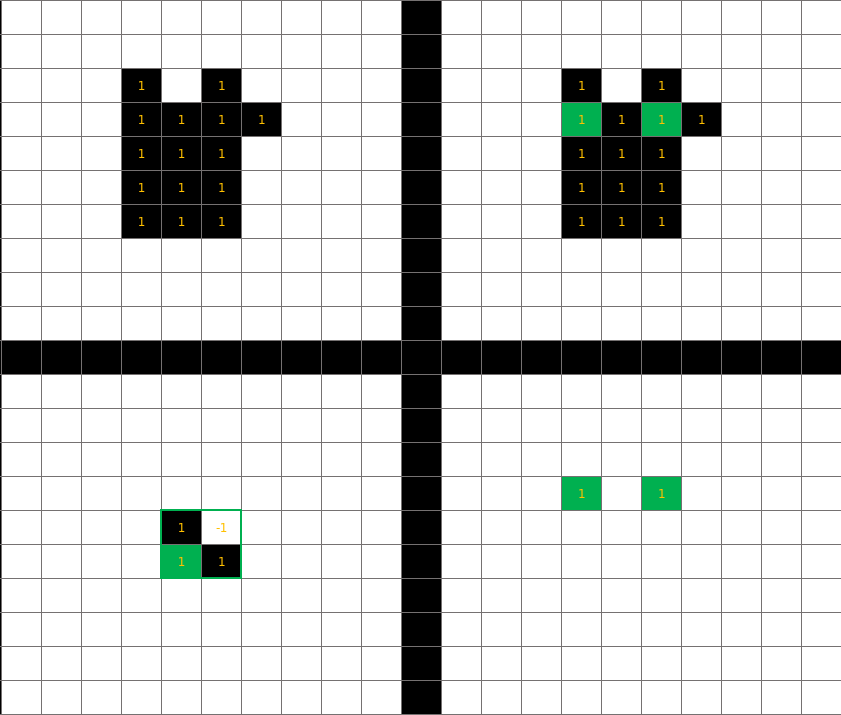
Note：在击中击不中变换的结构元中，-1表示背景，1表示前景，0表示不关心

‍

击中击不中变换的应用

‍

形状检测与识别：在工业检测中，用于检测产品表面特定形状的缺陷或标记，如检测电路板上的特定形状的焊点是否完整、有无缺陷等。通过设计合适的结构元素来匹配正常焊点的形状，利用击中击不中变换可以快速准确地找出不符合形状要求的焊点，从而实现产品质量的检测和控制。
纹理分析：在纹理图像分析中，某些纹理特征可能具有特定的形状或结构模式，击中击不中变换可以帮助提取这些纹理特征，用于图像分类、分割等任务。例如在分析纺织品的纹理时，检测其中特定的编织图案或纹理结构，以判断纺织品的质量和类型。
字符识别预处理：在光学字符识别（OCR）系统中，可作为预处理步骤，用于检测字符的特定结构部分，如字母中的孔洞（如字母“o”“p”等中的圆形孔洞）、笔画的端点和交叉点等特征，这些特征信息可以为后续的字符分类和识别提供重要依据，提高字符识别的准确性和效率。

‍

灰度形态学的基本运算

‍

灰度图像

‍

灰度图像与二值图像不同，它的像素值范围为 $x\in[0-255],x\in\mathbb{Z}$ ，能够表示图像的明暗变化、纹理等细节。

对于灰度图像 $f [x, y]$ ，我们可以通过阈值集合 $T_{\theta}(f[x,y])=\{[x,y]:f[x,y]\geq\theta\},-\infty<\theta<+\infty$ 来分解图像，原始图像可由 $f[x,y]=sup\{\theta:[x,y]\in T_{\theta}(f[x,y])\}$ 重建。

阈值集合表示的是图像中灰度值大于等于的 $\theta$ 所有像素点的集合。如果 $\theta=128$ ，那么 $T_{128}(f[x,y])$ 就是图像中所有灰度值大于等于 $128$ 的像素点的集合。

简单来说，对于灰度图像，我们可以通过一个叫做阈值化的操作来分解图像，然后可以通过 supremum 操作重建图像。

‍

Flat/一般腐蚀算子

‍

灰度形态学中，Flat腐蚀算子定义如下：

$g[x,y]=\min\{W^{(+)}\{f[x,y]\}\}:=erode(f,W)$

其中：

‍

$f [x, y]$ 是原始的灰度图像在坐标 $(x, y)$ 处的像素值
$W^{(+)}$ 是结构元素相关的邻域“窗口”算子
$g [x, y]$ 是腐蚀后的图像在坐标 $(x, y)$ 处的像素值

‍

其含义为，在图像的每个像素位置，取结构元素窗口 $W$ 内的最小值作为该像素的新值。

那么，图像中的暗区域就会扩大，而明亮区域就会缩小(因为变成小值了，越小越暗)。

也就是，暗大明小。

‍

灰度形态学中，一般腐蚀算子定义如下：

$g[x,y]=\inf_{\alpha,\beta}\{f[x+\alpha,y+\beta]-w[\alpha,\beta]\}=erode(f,w)$

这里 inf 表示取下确界(类似最小值)。

其含义为，对于图像 $f [x, y]$ 中的每个像素点 $(x, y)$ ，要在结构元素 $w[\alpha,\beta]$ 所覆盖的邻域内进行计算，即计算 $f[x+\alpha,y+\beta]$ （即图像在平移 $(\alpha,\beta)$ 后的像素值）与（结构元素在 $(\alpha,\beta)$ 位置的值）的差值，并取这些差值中的下确界作为像素点 $(x, y)$ 经过腐蚀后的新值 $g [x, y]$ 。

‍

Flat/一般膨胀算子

‍

灰度形态学中，Flat膨胀算子定义如下：

$g[x,y]=\max\{W^{(-)}\{f[x,y]\}\}:=dilate(f,W)$

与Flat腐蚀算子相反，它所做的是在图像的每个像素位置，取结构元素窗口 $W$ 内的最大值作为该像素的新值。

那么，图像中的明亮区域就会扩大，而暗区域就会缩小(因为变成大值了，越大越亮)。

也就是，明大暗小。

‍

灰度形态学中，一般膨胀算子定义如下：

$g[x,y]=sup_{\alpha,\beta}\{f[x-\alpha,y-\beta]+w[\alpha,\beta]\}=sup_{\alpha,\beta}\{w[x-\alpha,y-\beta]+f[\alpha,\beta]\}$

这里的 $s u p$ 表示取上确界（类似于取最大值）。对于图像 $f [x, y]$ 中的每个像素点 $(x, y)$ ，在结构元素 $w[\alpha,\beta]$ 的邻域内，计算 $f[x-\alpha,y-\beta]$ （图像平移 $(-\alpha,-\beta)$ 后的像素值）与 $w[\alpha,\beta]$ 的和，并取这些和中的上确界作为像素点 $(x, y)$ 经过膨胀后的新值 $g [x, y]$ 。

‍

Flat腐蚀和膨胀算子和一般腐蚀和膨胀算子

‍

从名字上可以猜到，Flat算子其实是一般算子的特殊情况。

用途上就是，没特殊需要或者精度要求就用Flat算子简单处理即可，否则就要使用计算更加复杂的一般算子来处理。

‍

形态学边缘检测(Morphological edge detectors)

‍

简要介绍

‍

我们知道，腐蚀去皮肉留下骨头，膨胀让骨头长出肉，那么我们将膨胀后的结果与腐蚀后的结果进行差异的比较，那么是不是就可以直接得到外面的皮肉的轮廓了？

正式点说，对原图像腐蚀会减小前景物体，对原图像膨胀会增大前景物体，那么两者的差异则是物体的边界轮廓。

但是有个前提如下：

‍

$erode(f,W)\neq f \space AND \space dilate(f,W)\neq erode(f,W)$

‍

在图像中，边缘检测可突出物体轮廓，有助于后续的目标识别、图像分割等任务，如检测图像中物体的边界。

‍

优点：保持边缘连通性，对噪声鲁棒性较好
缺点：边缘定位精度相对较低，依赖于结构元素的选择

‍

对于二值图像

‍

$g_{edge}[x,y] = g_{dilate}[x,y] \space XOR \space g_{erode}[x,y]$

‍

我们知道，二值图像只有 $\left\lbrace0,1\right\rbrace$ 两种值，那么我们将膨胀运算后的结果与腐蚀运算后的结果进行逻辑异或运算就可以精确地提取出边缘像素，进而直接显示出物体的轮廓边界。

‍

对于灰度图像

‍

$g_{edge}[x,y] = g_{dilate}[x,y] - g_{erode}[x,y]$

‍

参考资料

‍

data

‍

Lena图等: http://www.eecs.qmul.ac.uk/~phao/IP/Images/

检索到的出处: https://blog.csdn.net/nbu_dahe/article/details/114698790

‍

blog and related sources

‍

图像数学形态学的基本原理与代码实现（腐蚀、膨胀、开闭运算）：https://blog.csdn.net/deepsprings/article/details/107291741
第8章：形态学操作： https://blog.csdn.net/weixin_57440207/article/details/122647000
斯坦福大学Bernd Girod教授的《数字图像处理》课程的讲义: https://web.stanford.edu/class/ee368/Handouts/Lectures/2015_Autumn/7-Morphological_16x9.pdf