目录
介绍
算法思路
函数实现
函数声明
确定基准值
创建新函数
创建循环找数据(right,left)
交换左右数据
交换条件设置
外部循坏条件设置
初步总结代码
循环条件完善
内层循环的完善
外层循环的完善
相遇值大于keyi
相遇值等于keyi
相遇值小于keyi
确定基准值代码展示
递归左/右子序列
编辑
完整代码
总结
介绍
快速排序是Hoare于1962年提出的⼀种⼆叉树结构的交换排序⽅法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两⼦序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右⼦序列重复该过程,直到所有元素都排列在相应位置上为⽌。
算法思路
1)创建左右指针,确定基准值(keyi)
2)从右向左找出比基准值小的数据,从左向右找出比基准值大的数据,左右指针数据交换,进入下次循环
//递归遍历左子序列
QuickSort(arr, left, keyi - 1);
//递归遍历右子序列
QuickSort(arr, keyi + 1, right);函数实现
函数声明
void QuickSort(int* arr, int left, int right)对一个数组进行快速排序时,需要利用基准值取每个数组的左子序列和右子序列,然后进行递归、排序,最后返回。函数声明部分必须包含数组地址,左子序列和右子序列。

确定基准值
如何找基准值?
right:从右到左找到比基准值小的数据
left: 从左到右找到比基准值大的数据
创建新函数
新建一个函数 _QuickSort 来查找数组的基准值,函数参数和快速排序函数参数相同。
//用来查找基准值
int _QuickSort(int* arr, int left, int right)创建循环找数据(right,left)
创建一个数组为 int arr[] = {6,1,2,7,9,3} ,假设当前第一个有效数据为基准值keyi,left 为 keyi 后的一个有效数据,right 为最后一个有效数据。

创建二个循环,一个使 right 指向比基准值小的数据,一个使 left 指向比基准值大的数据。在设置循环条件时,需要将 arr[right] > arr[keyi] ,arr[left] < arr[keyi] 来保证循环能够正常运行。
while(arr[right] > arr[keyi])//等于该如何操作???
{
right--;//调整right位置,直到找到比arr[keyi]小的数据为止
}
//离开循环说明right已经找到正确的位置
while(arr[left] < arr[keyi])//等于该如何操作???
{
left++;//调整left位置,直到找到比arr[keyi]大的数据为止
}
//离开循环说明left已经找到正确的位置如果当 arr[right] / arr[left] == arr[keyi] 时,该如何操作???
交换左右数据
当循环结束后,left 和 right 指针都找到了需要进行交换的数据,然后进行交换操作
Swap(&arr[left], &arr[right]);//交换函数
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}交换条件设置
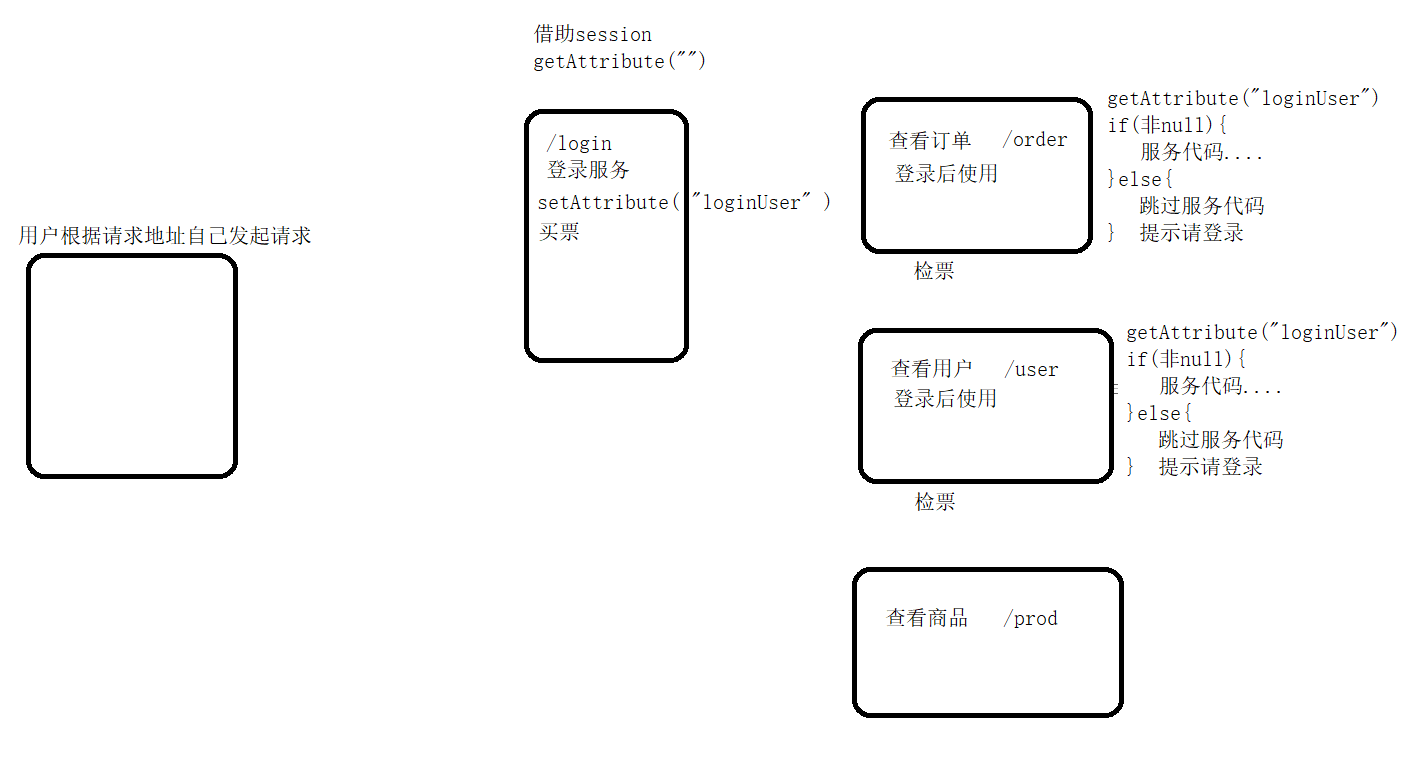
如图所示,在 left 和 right 完成第一次交换后,满足 left < right 的条件,进入到第二次循环,此时 right 找到了比 keyi 小的数据,left 找到了比 keyi 大的数据,这种条件下 left 和 right 是否还需要交换数据???

left 的作用是将比 keyi 大的数据移到数组右边,right 的作用是将比 keyi 小的数据移到数组左边,图示案例明显违背了以上作用,所以在交换数据时,需要判断 left 和 right 的位置。
if (left < right)
{
Swap(&arr[left], &arr[right]);
}
外部循坏条件设置
创建循环找到正确数据,并且进行交换后,只是完成了一组数据的交换,而后需要对更多的数据进行交换。
循环条件如何设置?
当 left > right 时,即right⾛到left的左侧,而 left 扫描过的数据均不大于keyi,因此 right 此时指向的数据一定不大于keyi ,所以就没有必要继续循环操作。
所以循环条件应该设置为:
while(left < right)//是否可以等于???当小的数据都普遍位于数组左边,大的数据都普遍位于数组右边时,交换 arr[right] 和 arr[keyi] ,此时的 right 指向的就是基准值。
Swap(&arr[keyi], &arr[right]);
return right;//基准值下标位置初步总结代码
将以上代码综合,得到以下函数:
int _QuickSort(int* arr, int left, int right)
{
int keyi = left;
++left;
while (left < right)//是否可以等于??
{
//right从右往左找到比基准值小的数据
while (arr[right] > arr[keyi])
{
right--;
}
//left从左往右找到比基准值大的数据
while (arr[left] < arr[keyi])
{
left++;
}
//此时left和right都找到了相对应的数据,进行交换操作
if (left < right)
{
Swap(&arr[left], &arr[right]);
}
}
Swap(&arr[keyi], &arr[right]);
return right;//基准值下标位置
}如代码所示,循环条件仍旧不够完善,没有考虑到等于的情况,现在我们开始完善代码。
循环条件完善
内层循环的完善
设置数组 int arr[] = {6,6,6,6,6,6} ,当数组数据全都相同时,我们假设内层循环条件 arr[right] >= arr[keyi],right 会一直往前遍历寻找比 keyi 小的数据,但是一直找不到,就会越界。
所以我们在进行内层循环的设置时需要加上一个条件,left <= right。

同理,当数组数据全都相同时,我们假设内层循环条件 arr[left] <= arr[keyi],left 会一直往后遍历寻找比 keyi 大的数据,但是一直找不到,就会越界。
所以在用 left 找比 keyi 大的数据时,循环也需要加上,left <= right。

//目前假设right和left所指向的数值可以等于keyi
while (left <= right && arr[right] >= arr[keyi])
{
right--;
}
while (left <= right && arr[left] <= arr[keyi])
{
left++;
}以该层代码来进行快速排序,right 在内层循环后来到 keyi 的位置,left 因为大于 right 无法进入循环,交换也无法实现,跳出循环后交换 right 和 keyi 的数据,发现基准值仍在最左端。
按照如此方法递归查找,发现该数组不存在左子序列,并且时间复杂度也比较差。快速排序用二分的方法去排序,这个事例表明内存循环时 arr[right] / arr[left] 不能等于 arr[keyi]。

所以在设置内层循环时,循环条件应该为:
while (left <= right && arr[right] > arr[keyi])
while (left <= right && arr[left] < arr[keyi])同时那我们该如何应对当 arr[right] / arr[left] == arr[keyi] 的情况呢?
当遭遇这种情况时,我们不仅无法进入 right 调整的循环,也无法进入 left 调整的循环,但是却符合 left < right 可以进入到交换的循环当中,因为缺少了对指针的调整,所以我们需要在交换完 left 和 right 的数据后主动++和--,以此来防止以外的发生。
if (left < right)//是否可以等于??
{
Swap(&arr[left++], &arr[right--]);//保证数据相等时left和right可以调整指向
}外层循环的完善
相遇值大于keyi
在此基础上,我们再对该循环进行检查。left 和 right 在完成两次交换后到达了相遇点,如果按照原本外层循环的代码来看,当 left == right 时,应当跳出循环,最后进行 keyi 与 right 的交换,但是相遇值却大于 keyi ,将 keyi 与其交换则会发生错误,使得大于基准值的数字在基准值的左边。

所以在设置外层循环的条件时,我们可以将 left == right ,使其进入到循环当中,right 满足条件--,来到下标为2的位置,此时 right <left ,无法进入内层循环与交换,则与 keyi 发生交换,以此确定了基准值的位置。
while (left <= right)
相遇值等于keyi
同理,如果当相遇值等于 keyi 时,我们可以进入到外层循环,却不能进入到内存循环,那我们只能从交换条件上入手。

我们可以利用交换函数中的调整参数来对 left 和 right 进行调整,前提是得满足 if 条件,当前 left == right ,所以我们需要将条件修改为 left <= right。

if (left <= right)
{
Swap(&arr[left++], &arr[right--]);
}相遇值小于keyi
当相遇值小于 keyi 时,原理和相遇值大于 keyi 一样,在外层循环条件为 while(left <= right) 时,进入外层循环,right 找到最小值为相遇点数值,left 往后++寻找,不满足left <= right的条件后跳出内层循环和外层循环,将 right 与 keyi 交换,找到正确的基准值。

确定基准值代码展示
int _QuickSort(int* arr, int left, int right)
{
int keyi = left;
++left;
while (left <= right)
{
//right从右往左找到比基准值小的数据
//如果数组数据全部相同,则需要变更循环条件
while (left <= right && arr[right] > arr[keyi])//加上条件使得基准值位置更加偏向于数组中央
{
right--;
}
//left从左往右找到比基准值大的数据
while (left <= right && arr[left] < arr[keyi])
{
left++;
}
//此时left和right都找到了相对应的数据,进行交换操作
if (left <= right)
{
Swap(&arr[right--], &arr[left++]);
}
}
Swap(&arr[keyi], &arr[right]);
return right;//基准值下标位置
}递归左/右子序列
设置一个数组,int arr[] = {6,1,2,7,9,3},进行快速排序演示。
第一次数据交换,right上3小于6,left上7大于6
right上3小于6,left在++时超过right,循环停止,不满足交换条件,跳出循环,right与keyi交换数据,6成为基准值。

递归左子序列,right上2小于3,left在++时超过right,循环停止,不满足交换条件,跳出循环,right与keyi交换数据,3成为基准值。

递归左子序列,right上1小于2,left在++时超过right,循环停止,不满足交换条件,跳出循环,right与keyi交换数据,2成为基准值。
递归左子序列,right上1等于1,跳出循环,不满足交换条件,right与keyi交换数据,1成为基准值。

当我们再去递归左子序列时发现,已经没有左子序列可以进行递归了,右子序列也无法递归,原因是当1为基准值时, 不满足以下条件:
//递归遍历左子序列
QuickSort(arr, left, keyi - 1);
//递归遍历右子序列
QuickSort(arr, keyi + 1, right);所以当 left > right 时,我们需要进行返回 。
void QuickSort(int* arr, int left, int right)
{
if (left > right)
{
return;
}
//确定基准值
int keyi = _QuickSort(arr, left, right);
//递归遍历左子序列
QuickSort(arr, left, keyi - 1);
//递归遍历右子序列
QuickSort(arr, keyi + 1, right);
}递归右子序列,right上7小于9,left在++时超过right,循环停止,不满足交换条件,right与keyi交换数据,9成为基准值。

再进行递归时发现,keyi+1大于right,keyi-1小于left,不符合规律,所以递归结束。

返回后可以发现,每次递归所得出的基准值都是每一个数字在其有序数组中应当存在的位置。
完整代码
int _QuickSort(int* arr, int left, int right)
{
int keyi = left;
++left;
while (left <= right)
{
//right从右往左找到比基准值小的数据
//如果数组数据全部相同,则需要变更循环条件
while (left <= right && arr[right] > arr[keyi])//加上条件使得基准值位置更加偏向于数组中央
{
right--;
}
//left从左往右找到比基准值大的数据
while (left <= right && arr[left] < arr[keyi])
{
left++;
}
//此时left和right都找到了相对应的数据,进行交换操作
if (left <= right)
{
Swap(&arr[right--], &arr[left++]);
}
}
Swap(&arr[keyi], &arr[right]);
return right;//基准值下标位置
}
//快速排序
void QuickSort(int* arr, int left, int right)
{
if (left > right)
{
return;
}
//确定基准值
int keyi = _QuickSort(arr, left, right);
//递归遍历左子序列
QuickSort(arr, left, keyi - 1);
//递归遍历右子序列
QuickSort(arr, keyi + 1, right);
}总结
快速排序【hoare版】运用到了递归的方法进行实现,代码数量不多,但是递归繁琐,所需要考虑的情况也分多种。对于循环条件设置和if条件设置上表现得极其严苛。