目录
- 一、560.和为K的⼦数组
- 1.1 前缀和
- 1.2 暴力枚举
- 二、974.和可被K整除的⼦数组
- 2.1 前缀和
- 2.2 暴力枚举
- 三、525.连续数组
- 3.1 前缀和
- 3.2 暴力枚举
- 四、1314.矩阵区域和
- 4.1 前缀和
- 4.2 暴力枚举

一、560.和为K的⼦数组
题目链接:560.和为K的⼦数组
题目描述:

题目解析:
- 求数组中子串的和为k的个数。
1.1 前缀和
解题思路:
- 假设已经创建好了一个前缀和数组dp,我们使用前缀和的时候,判断从0到 i 位置的和为k的子数组个数,只需要在dp下标[ 0 , i - 1 ]中找dp元素值为dp[ i ] - k的个数即可。
- 所以我们使用一个容器hash表来存储从0 到 i - 1的前缀和的个数,关键字key就是前缀和,values就是次数。
- 细节处理:
-
- 我们不需要真的使用前缀和数组,只需要遍历原数组时,用一个变量记录遍历过的元素和即可。
-
- 当该前缀和就是k的时候,我们上面条件没有考虑,所以我们还要先放入(0,1)表示这种情况。
解题代码:
//时间复杂度:O(n)
//空间复杂度:O(n)
class Solution {
public int subarraySum(int[] nums, int k) {
Map<Integer,Integer> hash = new HashMap<>();
hash.put(0,1);
int sum = 0;
int ret = 0;
for(int i = 0; i < nums.length; i++) {
sum += nums[i];
ret += hash.getOrDefault(sum-k,0);
hash.put(sum, hash.getOrDefault(sum,0)+1);
}
return ret;
}
}
1.2 暴力枚举
解题思路:
- 直接使用两层for循环,将每一种可能枚举出来。
解题代码:
//时间复杂度:O(n^2)
//空间复杂度:O(1)
class Solution {
public int subarraySum(int[] nums, int k) {
int ret = 0;
for(int i = 0; i < nums.length; i++) {
int sum = 0;
for(int j = i; j < nums.length; j++) {
sum += nums[j];
if(sum == k) {
ret++;
}
}
}
return ret;
}
}
二、974.和可被K整除的⼦数组
题目链接:974.和可被K整除的⼦数组
题目描述:

题目解析:
- 跟上一道题一样的思路,只不过这个是求能被整除的个数而已。
2.1 前缀和
解题思路:
- 同余定理:如果(a - b)% p == 0 那么a % p 和b % p值相等。
- Java中负数对正数取余修正:在Java中负数对正数取余余数会是负数,修正方法就是:(a % p + p)% p
- 使用hash表将i下标前的每一个前缀和与k的余数存入。
- 再看前面前缀和与当前 前缀和的余数相同的个数即可。
- 当[0 , i]本身前缀和余数为0的时候,就是一个符合条件的子数组。
解题代码:
//时间复杂度:O(n)
//空间复杂度:O(n)
class Solution {
public int subarraysDivByK(int[] nums, int k) {
int ret = 0;
Map<Integer,Integer> hash = new HashMap<>();
hash.put(0 % k , 1);
int sum = 0;
for(int x : nums) {
sum += x;
int key = (sum % k + k ) % k;
ret += hash.getOrDefault(key,0);
hash.put(key, hash.getOrDefault(key , 0) + 1);
}
return ret;
}
}
2.2 暴力枚举
解题思路:
- 直接遍历数组,在将遍历元素的和取余即可。
- 会超时。
解题代码:
//时间复杂度:O(n^2)
//空间复杂度:O(1)
class Solution {
public int subarraysDivByK(int[] nums, int k) {
int ret = 0;
for(int i = 0; i < nums.length; i++) {
int sum = 0;
for(int j = i; j < nums.length; j++) {
sum += nums[j];
if((sum % k + k) % k == 0) ret++;
}
}
return ret;
}
}
三、525.连续数组
题目链接:525.连续数组
题目描述:

题目解析:
- 要我们返回子数组中 0 和1 数量相等的最长子数组的长度。
3.1 前缀和
解题思路:
- 我们使用一个容器hash表,关键字key来记录原数组每个下标i中的1与0个数差,而values记录这个差值的最小下标。
- 注意边界情况,如果刚好整个数组满足条件,结果就是数组长 又等于nums.length-1 + 1所以我们初始一个(0,-1)
- 求长度的时候,我们在前面找到 j 下标与现在 i 下标关键字一样,那么数组区间就是[ j+1 , i ]
解题代码:
//时间复杂度:O(n)
//空间复杂度:O(n)
class Solution {
public int findMaxLength(int[] nums) {
int ret = 0;
int n = nums.length;
Map<Integer,Integer> hash = new HashMap<>();
hash.put(0,-1);
//前面1和0个数之差
int num = 0;
for(int i = 0; i < n; i++) {
if(nums[i] == 0) num--;
else num++;
if(hash.containsKey(num)) ret = Math.max(ret, i - hash.get(num));
else hash.put(num, i);
}
return ret;
}
}
3.2 暴力枚举
解题思路:
- 两层for循环遍历数组,记录每一个子数组中1和0的个数,
- 当个数相同的时候,更新结果。
- 会超时
解题代码:
//时间复杂度:O(n^2)
//空间复杂度:O(1)
class Solution {
public int findMaxLength(int[] nums) {
int ret = 0;
for(int i = 0; i < nums.length; i++) {
int oneNum = 0;
int zeroNum = 0;
for(int j = i; j < nums.length; j++) {
if(nums[j] == 0) zeroNum++;
else oneNum++;
if(oneNum == zeroNum) ret = Math.max(ret,j-i+1);
}
}
return ret;
}
}
四、1314.矩阵区域和
题目链接:1314.矩阵区域和
题目描述:

题目解析:
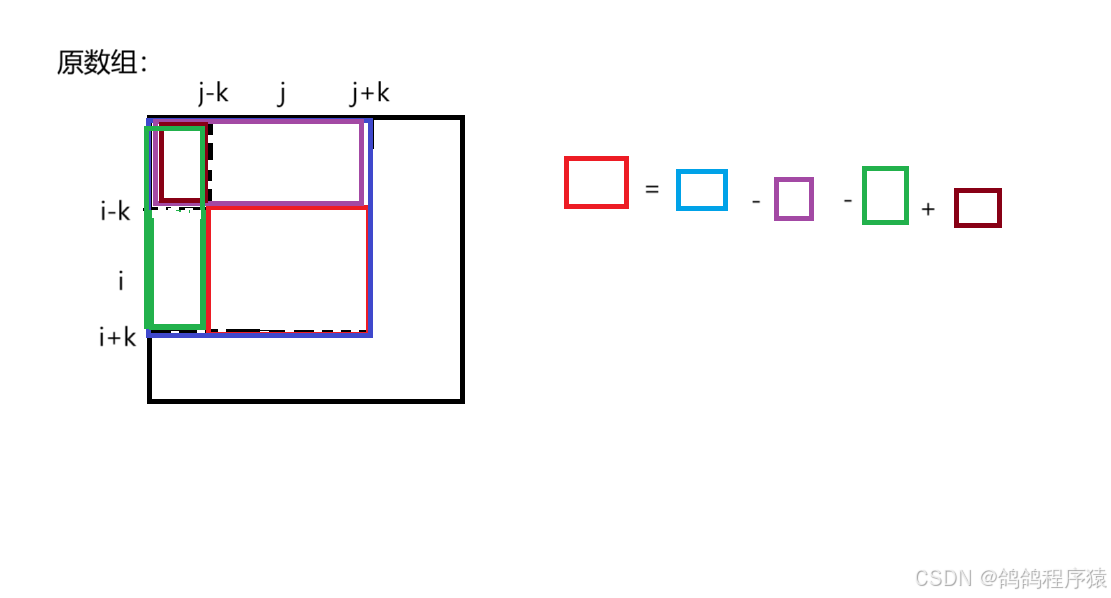
- 给一个二维数组,给一个k,返回的二维结果数组中数组( i , j )下标的值是原数组( i-k , j-k )到( i+k , j+k)的和。
- 就像下图中红方框框起来的:

4.1 前缀和
解题思路:
- 其实着就是前缀和上篇中给出的二维前缀和模版。
- 我们使用一个二维数组dp比原来数组多一行一列,dp[ i ][ j ]就是原数组中(0 , 0)到(i - 1 , j -1)的元素和。
- dp[ i ][ j ] = dp[ i - 1][j - 1] + nums[ i - 1][j - 1]。
- 在结果数组中与原数组大小一样,本来是求原数组( i-k , j-k )到( i+k , j+k)的和。那么对应到dp数组中,都要加1。
- 注意越界,如果( i-k , j-k )小于0那么就是0,i+k大于原数组行数,那么就是原数组行数,j+k大于原数组列数,那么就是原数组列数。
解题代码:
//时间复杂度:O(n^2)
//空间复杂度:O(n^2)
class Solution {
public int[][] matrixBlockSum(int[][] mat, int k) {
int n = mat.length;
int m = mat[0].length;
int[][] dp = new int[n+1][m+1];
dp[0][0] = mat[0][0];
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + mat[i-1][j-1];
}
}
int[][] ret = new int[n][m];
for(int i = 0; i < n; i++) {
for(int j = 0; j < m; j++) {
int x2 = i+k > n-1 ? n-1 : i+k;
int y2 = j+k > m-1 ? m-1 : j+k;
int x1 = i-k < 0 ? 0 : i-k;
int y1 = j-k < 0 ? 0 : j-k;
ret[i][j] = dp[x2+1][y2+1] - dp[x2+1][y1-1+1] - dp[x1-1+1][y2+1]+dp[x1-1+1][y1-1+1];
}
}
return ret;
}
}
4.2 暴力枚举
解题思路:
- 先两层for循环,拿到结果数组行列,
- 再两层for循环,求原数组( i-k , j-k )到( i+k , j+k)的和。
解题代码:
//时间复杂度:O(n^4)
//空间复杂度:O(1)
class Solution {
public int[][] matrixBlockSum(int[][] mat, int k) {
int n = mat.length;
int m = mat[0].length;
int[][] ret = new int[n][m];
for(int i = 0; i < n; i++) {
for(int j = 0; j < m; j++) {
int x2 = i+k > n-1 ? n-1 : i+k;
int y2 = j+k > m-1 ? m-1 : j+k;
int x1 = i-k < 0 ? 0 : i-k;
int y1 = j-k < 0 ? 0 : j-k;
for(int w = x1; w <= x2; w++) {
for(int q = y1; q <= y2; q++) {
ret[i][j] += mat[w][q];
}
}
}
}
return ret;
}
}