目录
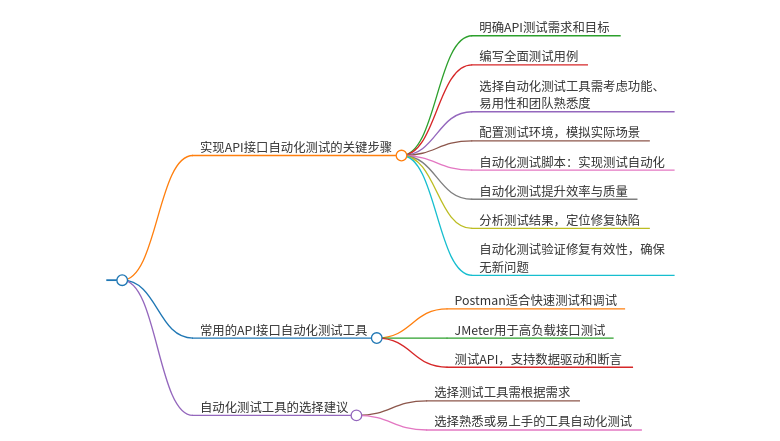
一、前言
二、 快排性能的关键点分析
三、 三路划分基本思想
四、 思路分析
五、提醒
六、代码实现
一、前言
继续对快速排序的深入优化进行探讨
二、 快排性能的关键点分析
决定快排性能的关键点是每次单趟排序后,key对数组的分割。
如果每次选key都能做到基本二分居中,那么快排的递归树就是棵均匀的满二叉树,性能最佳。虽然实践中不能做到每次都二分居中,但是性能也还是可控的。
但如果每次选到最大值/最小值,划分0个和n-1的子问题时,时间复杂度就为O(N^2),当数组序列有序时就会出现这样的问题。前面已经用三数取中or随机选key解决了该问题。
但是,有些场景下hoae和lomuto(前后指针法)还是适应的不是很好,就是当数组中有大量重复数据时,该场景下性能是有些退化的。
针对数组中有大量重复数据的问题,我们采用三路划分的方式来解决。
三、 三路划分基本思想
那什么是三路划分呢?
在之前快排是排完序把key放在中间,左边比key值小,右边比key大,跟key相等的值在哪里并没有规定,跟key相等的值可以在左边,也可以在右边。
三路划分的基本思想是将数组分为三个部分:
当面对有大量跟key相同的值时,三路划分的核心思想类似hoare的左右指针和lomuto的前后指针的结合。核心思想是把数组中的数据分为三段:
小于基准元素key的放在左边
等于基准元素key的全部放在中间
大于基准元素key的放在右边
所以叫做三路划分算法。
通过三路划分的方式,可以避免在数组中有大量重复元素时出现的性能问题。
四、 思路分析
基本思路如下:
这里跟lomuto的前后指针法相结合(排升序)
- key默认取left位置的值
- left指向区间第一个元素位置,right指向区间最后一个元素位置,cur指向left+1的位置
- 对cur进行判断
- 如果cur<key,cur指向的值与left位置的值进行交换,然后left++,cur++
- 如果cur>key,cur指向的值与right位置的值进行交换,然后right--
- 如果cur==key,cur++
- 直到cur>right结束,排完单趟
结合图进行分析:

五、提醒
为什么cur==right要继续呢?
因为假如cur没有遇见比key大的值,right没有--,那么cur与right在相同位置时,并不能确定right所指向的值是否小于key。
例如下图的情况:

六、代码实现
//交换算法
void swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//三数取中
int GetMidi(int* a, int left, int right)
{
int midi = (left + right) / 2;
if (a[left] > a[right])
{
if (a[left] < a[midi])
{
return left;
}
else if (a[midi] < a[right])
{
return right;
}
else
{
return midi;
}
}
else
{
if (a[right] < a[midi])
{
return right;
}
else if (a[midi] < a[left])
{
return left;
}
else
{
return midi;
}
}
}
//三路划分算法
void QuickSort_Three_Way_Partition(int* a, int left, int right) //参数为数组下标
{
if (left >= right)
{
return;
}
int midi = GetMidi(a, left, right);
swap(&a[left], &a[midi]);
int begin = left;
int end = right;
int key = a[left];
int cur = left + 1;
while (cur <= end)
{
if (a[cur] < key)
{
swap(&a[cur], &a[begin]);
begin++;
cur++;
}
else if (a[cur] > key)
{
swap(&a[cur], &a[end]);
end--;
}
else if (a[cur] == key)
{
cur++;
}
}
//递归左右区间
QuickSort_Three_Way_Partition(a, left,begin-1);
QuickSort_Three_Way_Partition(a, end+1, right);
}
int main()
{
int arr[] = {7,13,6,2,7,7,23,7,7,98,11,6,9,1,66,21,5};
int sz = sizeof(arr) / sizeof(arr[0]);
QuickSort_Three_Way_Partition(arr,0,sz-1);
return 0;
}