🏰代码及环境配置:请参考 环境配置和代码运行!
4.1.1 基础概念
4.1.1.1 Configuration Space(配置空间)
- configuration: 机器人上每一点位置的完整说明
- degrees of freedom: 机器人能够独立移动或旋转的关节数量(下图所示有4个自由度)
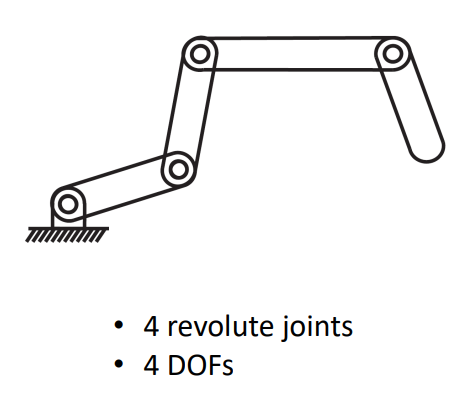
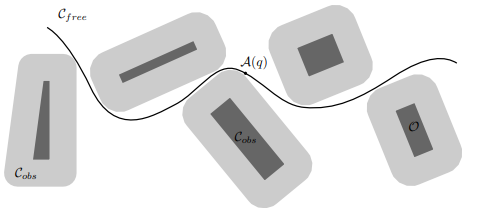
- configuration space(C-space): 机器人所有可能配置的n维空间,在C-space中,机器人的每个configuration就是一个点,下图即为一个机器人的configuration space,其中 A ( q ) A(q) A(q)是机器人的configuration,白色区域对于 A ( q ) A(q) A(q)是安全的,浅灰色区域是 A ( q ) A(q) A(q)和障碍物之间可能的碰撞区域。
4.1.1.2 C-space Obstacle
-
Planning in workspace
workspace就是机器人真实的一个工作空间,即我们所处的物理世界。但如果在workspace中进行机器人的路径规划是比较麻烦的,主要是由于:
- 每个机器人拥有不同的形状和大小
- 碰撞检测需要知道机器人的几何信息
-
Planning in C-space
- 在C-space中,机器人可以抽象为一个点
- 感知到的障碍物信息可以提前部署到C-space中,我们成为C-obstacle
- 此时,可以将C-space分为自由空间C-free和障碍物空间C-obstacle,即 C s p a c e = ( C o b s t a c l e ) U ( C f r e e ) C_{space} = (C_{obstacle})\ U\ (C_{free}) Cspace=(Cobstacle) U (Cfree)
- 然后路径规划就可以在C-free中找一个连接 q s t a r t q_{start} qstart和 q g o a l q_{goal} qgoal的路径
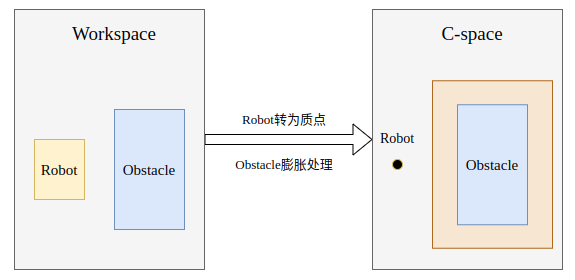
如下图:我们将在workspace中的规划问题转为C-space下的规划问题,此时在路径规划时,将机器人当成一个点来处理,极大地降低复杂度。
4.1.2 图
图是一种抽象的数据结构,用于表示对象之间的关系或连接。它由节点(也称为顶点)和边组成,节点代表实体或对象,而边则表示这些实体或对象之间的某种关系或连接。
4.1.2.1 图的基本组成
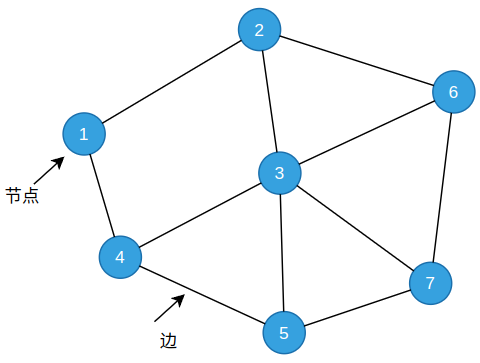
- 节点(Vertex):图中的基本元素,通常表示为圆圈、点或任何其他形状的符号。节点可以代表任何事物,如人、地点、事物、概念等。
- 边(Edge):连接两个节点的线段或箭头,表示这两个节点之间存在某种关系或连接。边可以是有向的(表示单向关系)或无向的(表示双向关系)。
4.1.2.2 图的类型
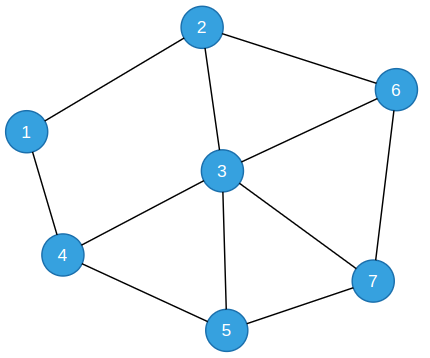
- 无向图(Undirected Graph):图中的边都是无向的,即没有箭头表示方向。在无向图中,如果两个节点之间有边相连,则它们是相邻的。
- 有向图(Directed Graph):图中的边都是有向的,即每条边都有一个箭头表示方向。在有向图中,如果两个节点之间有一条从A指向B的边,则称A是B的前驱,B是A的后继。
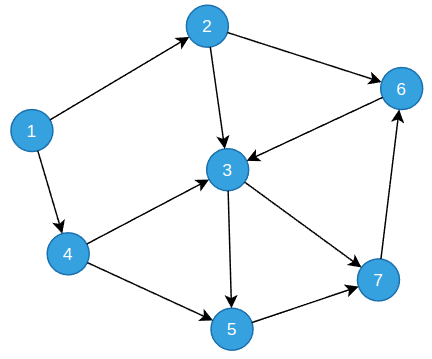
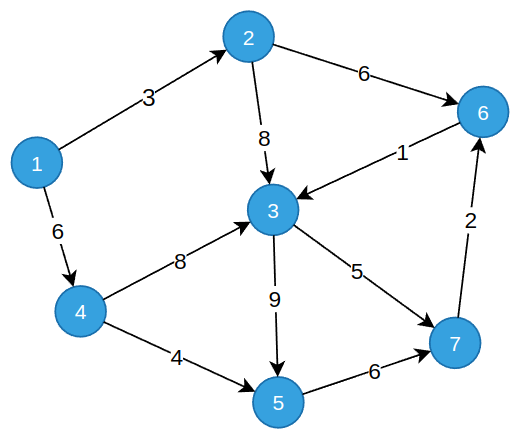
- 加权图(Weighted Graph):图中的每条边都有一个与之相关联的权值(也称为权重或成本),表示两个节点之间连接的某种度量或代价。
4.1.2.3 图的表示方法
图可以用多种方式进行表示,常见的表示方法有邻接矩阵和邻接表两种。
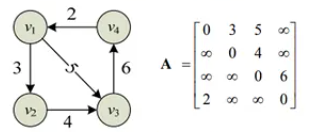
- 邻接矩阵(Adjacency Matrix):使用二维数组来表示图。数组的行和列分别对应图中的节点,数组中的元素表示节点之间是否存在边以及边的权重(对于加权图)。
下图为带权有向图的邻接矩阵:
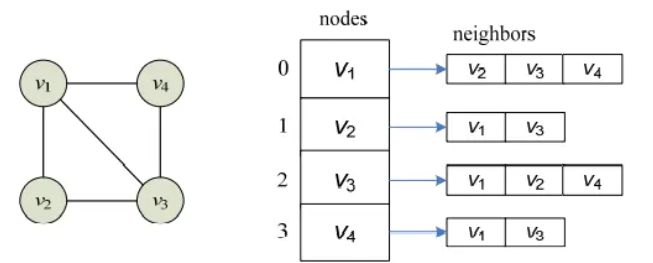
- 邻接表(Adjacency List):使用数组或链表的数组来表示图。每个节点对应一个链表或数组,链表中存储与该节点直接相连的节点以及边的权重(对于加权图)。
下图为无向图的临接表:
4.1.2.4 状态空间图(State Space Graph)
- 状态空间图是搜索算法的数学表示,用于将问题抽象成图的形式。
- 每一个搜索问题都有一个对应的状态空间图。
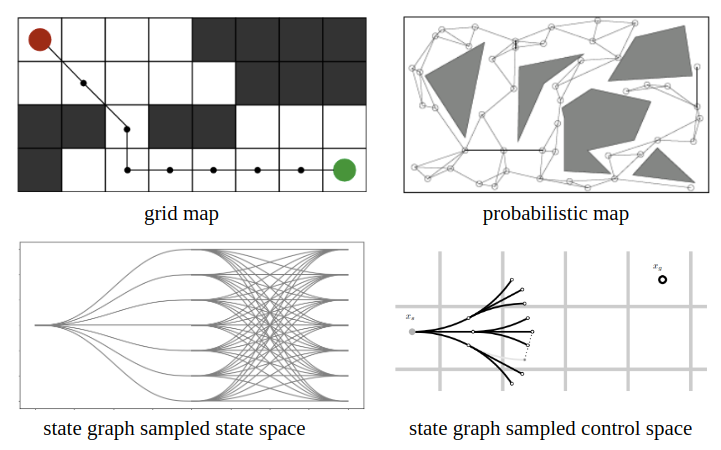
- 常见的状态空间图有:grid map,probabilistic map, state graph sampled state space和state graph sampled control space等,如下图所示:
4.1.3 图搜索概述
基于图搜索的大致流程如下:
- 维护一个container去存储将要访问的节点
- container初始化的时候只有起始节点 x s t a r t x_{start} xstart
- 开始循环
- 从container中取出一个节点,取出的规则需要遵循提前定义好的reward function
- 获得取出节点的所有邻节点
- 将所有的邻节点放入container
- 结束循环
其中核心在于如何以高效的方式从container中取出正确的节点,以便尽快达到目标状态,基于此,我们在接下来将介绍以下几种搜索算法 —— DFS (深度优先搜索) 、BFS (广度优先搜索)、Dijkstra、A*、Hybrid A*等。
推荐阅读
- 端到端理论与实战
- 动手学轨迹预测
- 动手学运动规划
- 动手学行为决策
- 强化学习入门笔记