标准正态分布的数据 tensorflow 实现正态分布图，python 编程，数据分析和人工智能...

news2024/11/28 0:41:22

import tensorflow as tf
 import matplotlib.pyplot as plt# 设置随机种子以获得可重复的结果
 tf.random.set_seed(42)# 生成正态分布的数据
 # mean=0 和 stddev=1 表示生成标准正态分布的数据
 # shape=(1000,) 表示生成1000个数据点
 data = tf.random.normal(mean=0, stddev=1, shape=(1000,))# 将Tensor转换为NumPy数组，以便Matplotlib可以处理
 data_np = data.numpy()# 绘制直方图
 plt.figure(figsize=(8, 6))  # 设置图形的大小
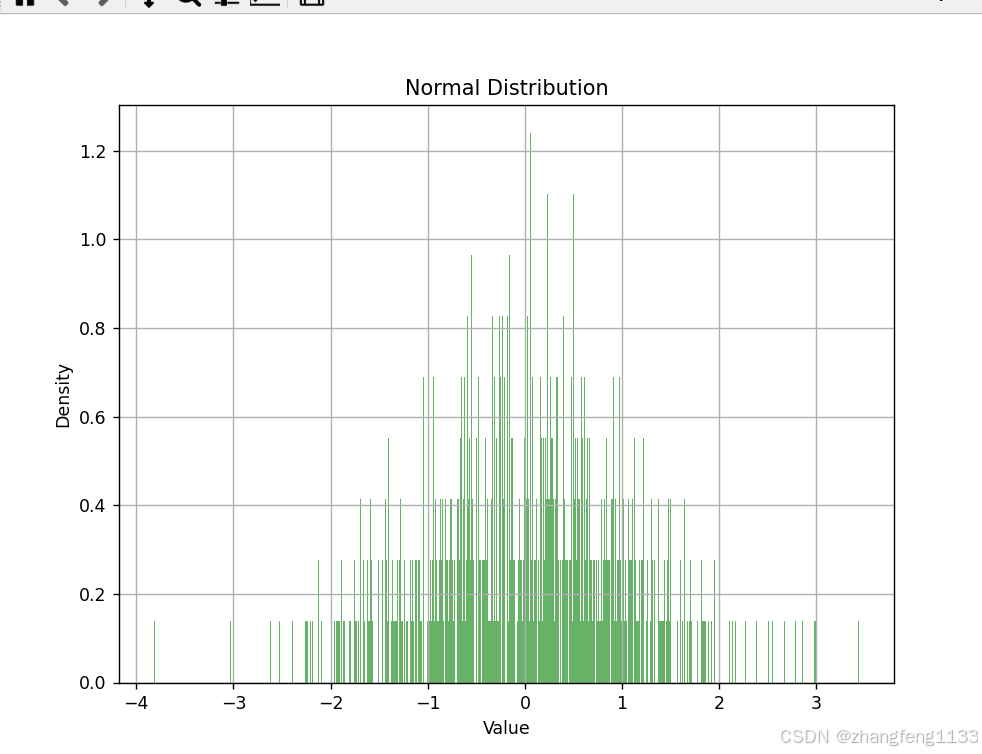
 plt.hist(data_np, bins=30, density=True, alpha=0.6, color='g')  # bins=30 表示分成30个柱状区域
 plt.title("Normal Distribution")  # 设置标题
 plt.xlabel("Value")  # 设置x轴标签
 plt.ylabel("Density")  # 设置y轴标签
 plt.grid(True)  # 显示网格# 显示图形
 plt.show()

标准正态分布的数据 tensorflow 实现正态分布图，python 编程，数据分析和人工智能_python

标准正态分布的数据 tensorflow 实现正态分布图，python 编程，数据分析和人工智能_python_02

import tensorflow as tf
import matplotlib.pyplot as plt

# 设置随机种子以获得可重复的结果
tf.random.set_seed(42)

# 生成正态分布的数据
# mean=0 和 stddev=1 表示生成标准正态分布的数据
# shape=(1000,) 表示生成1000个数据点
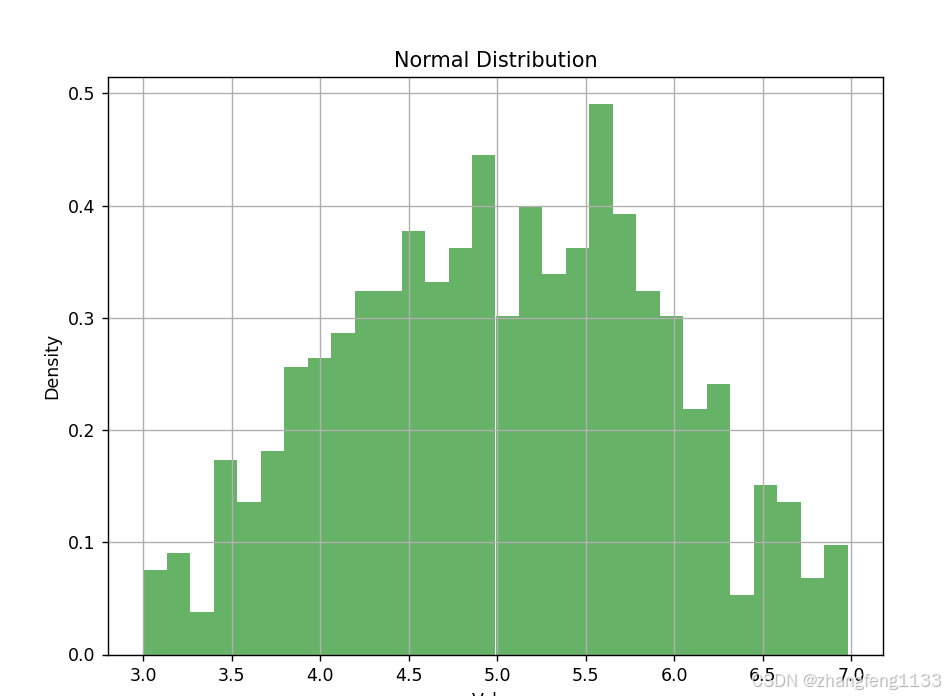
data = tf.random.normal(mean=0.5, stddev=0.5, shape=(1000,))
# data = tf.random.truncated_normal(mean=5, stddev=1, shape=(1000,), lower=-2, upper=2)
# data = tf.random.truncated_normal(mean=0.5, stddev=0.15, shape=(1000,), minval=0, maxval=1)

# # 使用 Sigmoid 函数进行变换
# data = tf.sigmoid(data)
# 手动截断超出0和1的值
# data = tf.clip_by_value(data, clip_value_min=0, clip_value_max=1)
# 将Tensor转换为NumPy数组，以便Matplotlib可以处理
data_np = data.numpy()

# 绘制直方图
plt.figure(figsize=(8, 6))  # 设置图形的大小
plt.hist(data_np, bins=30, density=True, alpha=0.6, color='g')  # bins=30 表示分成30个柱状区域
plt.title("Normal Distribution")  # 设置标题
plt.xlabel("Value")  # 设置x轴标签
plt.ylabel("Density")  # 设置y轴标签
plt.grid(True)  # 显示网格

# 显示图形
plt.show()

如果要一些自定义的特殊的分布图，如下

标准正态分布的数据 tensorflow 实现正态分布图，python 编程，数据分析和人工智能_学习_03

from __future__ import absolute_import, division, print_function, unicode_literals

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler

"""
图 3 展示了建议的 GAN 结构。与普通 GAN 不同，本研究在 FSO 信道模型中采用了条件 GAN(CGAN)[19]。
为了学习信道响应分布 p(y|x)，输入信号 x 被转换成条件向量 x̂，作为输出信号 y 的标签。噪声向量符合正态分布 z~N(0,1)
，其长度设为 52，以确保生成满足 p(y|x) 的任意数据。因此，经过竞争对抗训练后，生成器可以等价于信道模型，
并在输入数据 x 的条件下生成新的信道输出数据

"""
import csv
import sys

from tqdm import trange

sys.path.append('/home/aistudio/external-libraries')

"""
错误信息表明在训练一个自编码器模型时出现了问题，具体是在计算分类准确度(categorical_accuracy)时，y_true 和 y_pred 的维度不匹配。y_true 的形状是 [500]，而 y_pred 的形状是 [8000]。这通常发生在模型的输出层和标签数据的形状不一致时。

在这种情况下，你需要确保模型的输出层的维度与你的标签数据的维度相匹配。如果你的任务是多分类问题，并且每个类别都有一个唯一的整数标签(即标签是稀疏的)，那么你可以使用 sparse_categorical_crossentropy 作为损失函数，并使用 sparse_categorical_accuracy
作为评估指标。这样，你的模型输出层的维度应该与类别的数量相匹配。

例如，如果你有10个类别，模型的输出层应该有10个神经元，每个神经元对应一个类别的得分。然后，你可以使用 tf.keras.layers.Dense(10, activation='softmax') 来确保输出是10个类别的概率分布。

如果你的标签是 one-hot 编码的，那么你应该使用 categorical_crossentropy 作为损失函数，并使用 categorical_accuracy 作为评估指标。在这种情况下，y_true 应该是一个形状为 [batch_size, num_classes] 的张量，其中 num_classes 是类别的数量。

请检查你的模型结构和标签数据，确保它们的维度是一致的。如果你的模型输出是多维的，你可能需要使用 tf.keras.layers.Flatten() 层来将输出展平，以匹配标签数据的形状。

此外，如果你的模型是一个自编码器，并且你的目的是重构输入数据，那么你需要确保编码器的输出和解码器的输出与输入数据的形状相匹配。这通常意味着你的自编码器的输出层应该有与输入数据相同数量的神经元。

"""
# 导入必要的库


import subprocess  # 用于执行系统命令
import numpy as np  # 数学运算
import matplotlib.pyplot as plt  # 绘图库
import warnings  # 警告控制

from keras import models

with warnings.catch_warnings():
    warnings.filterwarnings("ignore", category=FutureWarning)  # 忽略未来警告
    import tensorflow as tf  # 导入 TensorFlow
import os  # 操作系统接口
from tensorflow import keras  # 导入 Keras
import time  # 时间库
import pandas as pd  # 数据处理库
import sys  # 系统相关的操作和参数

# 确保 Python 版本
assert sys.version_info >= (3, 5)

import matplotlib as mpl  # 导入 matplotlib 设置

# 设置 matplotlib 的参数
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)

# 打印 TensorFlow 版本
print(tf.__version__)

import tensorflow as tf
from tensorflow import keras
# from sklearn.preprocessing import OneHotEncoder
# import pandas as pd
from scipy import special

# 设置随机种子以确保结果可复现
np.random.seed(42)
tf.random.set_seed(42)

# 初始化参数
k = 4  # 每个消息的信息位数
M = 2 ** k  # 消息空间大小
n = 64  # 每个消息使用的实数通道数
print(M)  # 打印 M 的值

feature_num = n  # 批大小
batch_size = 100

SNR = 7  # 信噪比(dB)
randN_initial = keras.initializers.RandomNormal(mean=0.0, stddev=0.05, seed=None)  # 初始化器
hist_range = 2
# 因为运行多次，需要弄个均值
output_hist = tf.random.normal([1, 100], mean=0.2, stddev=0.05)
output_hist2 = tf.random.normal([1, 100], mean=1, stddev=0.24)
# inputs_hist = np.mean(inputs, axis=0)
# fake_output_hist1 = np.reshape(output_hist, [-1, ])
fake_output_hist1 = output_hist
plt.figure()
plt.hist(fake_output_hist1, bins=100, range=(-hist_range, hist_range), density=True, histtype='step')
plt.hist(output_hist2, bins=100, range=(-hist_range, hist_range), density=True, histtype='step')
plt.title("noise distribution")
plt.legend(["generator", "target"])
# plt.savefig(f'training_samples/wgan_fso_tf_epoch_{epoch}.png')
plt.show()
plt.close()