卡方检验是以卡方分布为基础,针对定类数据资料的常用假设检验方法。其理论思想是判断实际观测到的频数与有关总体的理论频数是否一致。
卡方统计量是实际频数与理论频数吻合程度的指标。卡方值越小,表明实际观察频数与理论频数越接近,反之卡方值越大则表示两者相差越大。卡方检验原假设实际频数与理论频数相同,依据卡方分布计算显著性p值进行统计结论的推断。取显著性水平α=0.05,当p值小于0.05时说明观察频数与理论频数差异有统计学意义,反之若p值大于0.05则说明观察频数与理论频数无差异。
一、方法概述
1. 应用方向
实际研究分析中,卡方检验有独立性/差异性检验和卡方拟合优度检验这两个重要的应用方向。
(1) 独立性/差异性检验
独立性检验可理解为判断两组或多组计数资料是相互关联还是彼此独立,如是否患病与是否吸烟的关联关系。根据研究侧重点的不同,也可用于两组或多组样本的总体率(或构成比)之间的差别是否具有统计学意义,如某疾病联合化疗和单纯化疗两种治疗方式的存活率有无差异,吸烟与不吸烟两组人群患病率有无差异。
(2) 拟合优度检验
检验实际观察的类别频数分布比例与已知类别频数分布比例是否符合的分析方法,通俗讲即检验验总体是否服从某个指定分布。比如在研究牛的相对性状分离现象时,用黑色无角牛和红色有角牛杂交,子二代出现黑色无角牛192头,黑色有角牛78头,红色无角牛72头,红色有角牛18头。这两对性状是否符合孟德尔遗传规律中9:3:3:1的遗传比例。
2. 数据要求
用于卡方检验的数据录入格式有两种。第一种是列联表频数资料,即加权数据格式,在分析时需要提前用频数进行加权。第二种是原始数据记录,即普通数据格式,在分析时软件工具会自动汇总频数结果。
实践中,列联表频数数据较为常见。列联表也叫交叉表,是两个分类变量各水平两两交叉组合后的频数汇总表。
如果两个分类变量均为2水平,那么二者构成2×2交叉表,交叉组合频数所在的位置也叫做单元格,因此2×2交叉表共有4个单元格,也就是常说的四格表。除四格表之外的列联表,我们可以统称为R×C列联表,其中R代表行个数,C代表列个数。
3. 卡方检验的类型
按列联表的形式,卡方检验可以简单划分为2×2四格表卡方检验、R×C列联表卡方检验;按研究设计不同,包括成组设计的独立性卡方检验和配对卡方检验;按研究目的,可以分为卡方拟合优度检验及独立性卡方检验。此外根据是否有分层变量,还包括分层卡方检验。各种类型卡方检验的应用目的、方法选择见表 4-23。
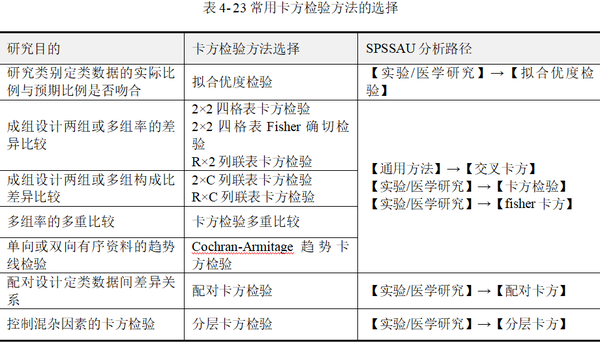
一般说卡方检验时,默认计算的是Pearson卡方统计量,而实际分析时,在2×2四格表卡方检验、R×C列联表卡方检验中通常会计算多个卡方统计量,包括Pearson卡方、Yates校正卡方(连续校正卡方)、趋势卡方,以及Fisher卡方检验(Fisher确切概率)等,应注意区分不同卡方统计量及其检验的适用条件,根据条件选择恰当的结果进行解释和分析。
使用SPSSAU进行卡方检验时,应注意【通用方法】→【交叉(卡方)】模块只提供较大样本时最常用的Pearson卡方检验,而【实验/医学研究】→【卡方检验】,模块可提供Pearson卡方、Yates校正卡方,以及Fisher卡方检验,适合小样本数据。
二、2×2四格表卡方检验
四格表是最基础的列联表,四格表卡方检验也是最常见的一种。本节介绍的是成组设计的四格表卡方检验,具体分析时需区分Pearson卡方、Yates校正卡方(连续校正卡方),以及Fisher卡方检验(Fisher确切概率)。其适用条件如表 4-24所示。
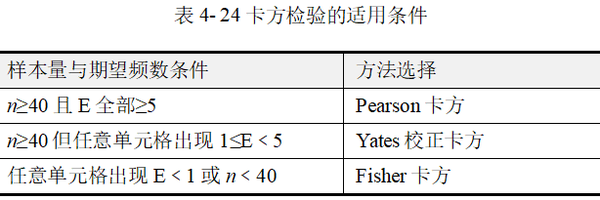
上表中n为样本量,E为理论频数。在四格表资料中,Pearson卡方适用于n≥40 且全部单元格 E≥5的情况。如果四格表 n≥40但任意单元格出现1≤E﹤5,则一般考虑采用Yates校正卡方,它是对Pearson卡方的校正结果。如果四格表中任意单元格出现E﹤1或n﹤40,则应当采用Fisher卡方(方积乾,2012)。
一般建议采用【实验/医学研究】→【卡方检验】模块来实现成组设计的四格表卡方检验。
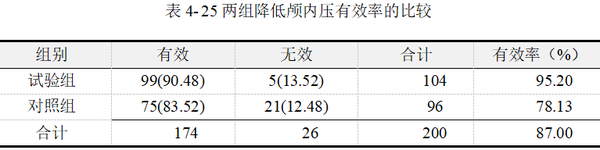
【例4-9】某医院欲比较异梨醇口服液(试验组)和氢氯噻嗪+地塞米松(对照组)降低颅内压的疗效。将200例颅内压增高症患者随机分为两组,结果见表 425。问两组降低颅内压的总体有效率有无差别?数据来源于孙振球,徐勇勇(2014),数据文档见“例4-9.xls”
1) 数据与案例分析
本例为频数资料,使用SPSSAU进行分析时,应按照加权数据格式录入数据。“组别”、“疗效”为均有2个水平的分类变量,“频数”为定量数据。在具体分析时需要将“频数”作为权重进行加权。本例加权数据格式见表 4-26。
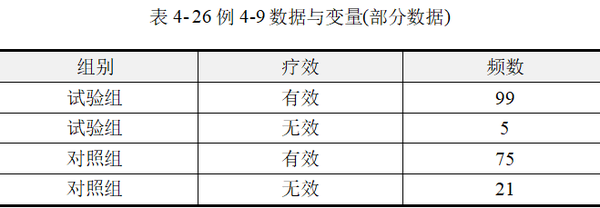
本例目的在于比较试验组与对照的治疗有效率,是典型的两组率的差异检验。数据资料为四格表频数资料,采用四格表卡方检验进行分析。
2) 卡方检验
读入数据后,仪表盘中依次选择【实验/医学研究】→【卡方检验】模块,将“组别”拖拽至【X(定类)】,“疗效”拖拽至【Y(定类)】。本例需加权处理,故再把“频数”拖拽至【加权项(可选)】。选项框内模型选择【百分数(按列)】,操作界面如图 414所示,最后单击【开始分析】。
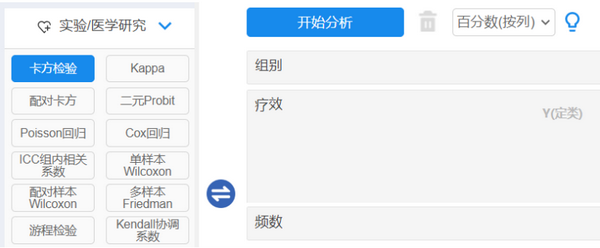
图 4-14 卡方检验操作界面
3) 结果解读
为方便理解不同卡方统计量及其检验的适用条件,可先对卡方检验卡方统计量、期望频数E,样本容量n进行统计汇总,其结果见表 4-27,最后按表 4-27的常见三线表格式对结果进行报告。
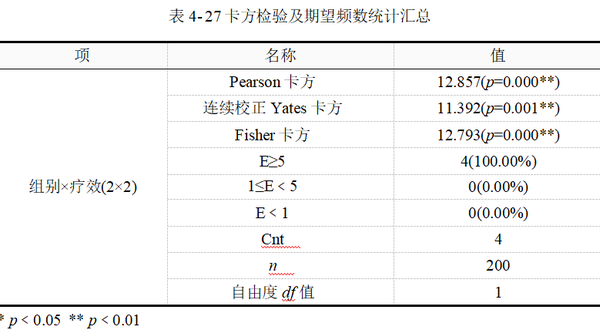
上表中包括了Pearson卡方、连续校正Yates卡方和Fisher卡方统计量及显著性p值,以及期望频数等基本信息的汇总结果。E为列联表单元格期望频数,n为样本量。本例中,样本量为200例,所有单元格的期望频数均大于5。根据卡方检验适用条件,应选择读取Pearson卡方检验结果。即卡方值12.857,p值﹤0.01,认为试验组与对照组两组人群的治疗有效率差异有统计学意义。
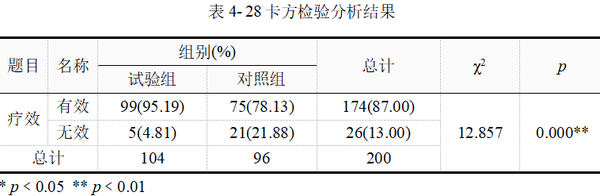
表 4-28最后两列给出的卡方统计量和p值,χ2=12.857,p值﹤0.01,其结果为平台自动匹配选择输出的Pearson卡方检验。
结合以上分析,可知试验组和对照组在降低颅内压的疗效并不相同。试验组有效率95.19%,对照组有效率78.13%。经Pearson卡方检验,按α=0.05水平,认为两组降低颅内压总体有效率不相等,具体表现为异梨醇口服液的有效率高于和氢氯噻嗪+地塞米松的有效率。
本例样本量和期望频数条件满足Pearson卡方检验的适用性,如果在四格表中有单元格出现期望频数在1~5之间的情况,则表 4-27会自动选择输出Yates校正卡方(连续性校正卡方检验)结果。一般建议读者直接读取和使用表 4-27的结果进行报告。
三、R×C表卡方检验与多重比较
R×C列联表卡方检验,包括常见的2×C两组构成比的差异比较;R×2两组或多组率的差异比较,还有多行多列即R×C列联表卡方检验。
本节内容介绍列联表中行与列两个变量均为无序多分类变量的情况,常见R×C卡方的应用场景见表 4-29。
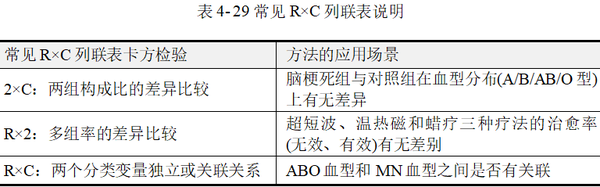
R×C列联表卡方检验时仍然采用的是Pearson卡方,其适用条件要求列联表中所有的单元格理论频数不应小于1,并且1≤E﹤5的单元格数量不宜超过总数的1/5。如果出现不符合该条件的情况,研究者可能要考虑采用Fisher确切概率法(方积乾,2012)。
R×C表卡方检验的结论是总体上差异是否显著,如果还想进一步判断两两总体率的差异,应继续做卡方结果的多重比较。在进行卡方检验时,【实验/医学研究】→【卡方检验】功能模块会根据分组情况自动实现卡方分割法多重比较。
以R×2列联表为例,卡方分割的基本思想是将R×2拆分为多个2×2四格表资料从而实现两两比较。例如3×2列联表检验3组总体率的差异,假设3个组名称分别为A/B/C,可拆分出AB(A、B两组率的比较)、AC、BC共3个2×2四格表卡方检验。
多重比较时,检验次数增多会增加Ⅰ类错误的概率,此过程应当对卡方检验p值进行校正,建议使用校正显著性水平(Bonferroni校正),假设显著性水平为0.05,当两两比较次数为3次时,那么Bonferroni校正显著性水平为0.05/3次=0.0167,即p值需要与0.0167进行对比,从而作出统计推断,而不是与0.05比较。
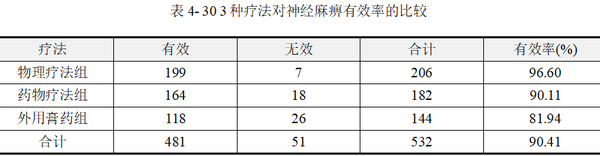
【例4-10】某医师研究物理疗法、药物治疗和外用膏药3种疗法治疗周围性面神经麻痹的疗效,数据资料见表 430。问3种疗法的有效率有无差别。数据来源于孙振球,徐勇勇(2014),本例数据文档见“例4-10.xls”。
1) 数据与案例分析
数据包括“组别”、“疗效”、“频数”3个变量,为加权数据格式。在表 430最后一列已经计算各组疗法的疗效有效率,依次为96.6%、90.11%、81.94%,本例目的比较3种不同治疗方法的疗效差异,为多组率的差异比较,接下来进行R×2卡方检验。
2) 卡方检验
读入数据后,依次选择【实验/医学研究】→【卡方检验】模块,将“组别”拖拽至【X(定类)】,“疗效”拖拽至【Y(定类)】。本例需加权处理,故再把“频数”拖拽至【加权项(可选)】。选项框内模型选择【百分数(按列)】,最后单击【开始分析】。
和上一例一样,表 4-31用于根据期望频数、样本量等适用条件选择正确的统计量和检验结果,表 4-32用于科研写作结果报告,也可以直接解释和分析表 4-32的结果。
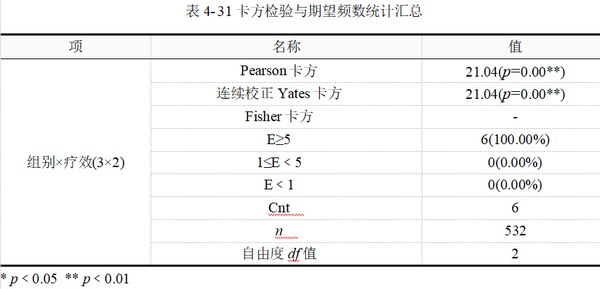
本例所有单元格E≥5,样本量532,依据卡方检验的适用条件,本例选择Pearson卡方检验结果,即卡方=21.04,p﹤0.01。
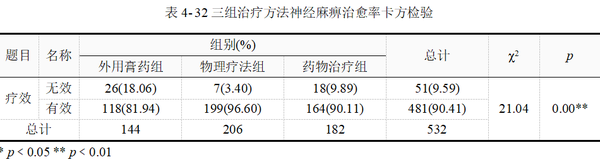
上表结果可直接用于报告,χ²=21.04,p值﹤0.01,说明3种疗法治疗周围性面神经麻痹的有效率有差别。
卡方检验时常使用相关性指标作为效应量的估计,如果研究上需要报告组别的效应量,可结合数据类型及交叉表格类型综合选择。如表 4-33所示,本例选择Cramer v效应量,此处Cramer v为0.2,说明存在弱相关。

综合以上信息,本例比较3组治疗方法的疗效。结果显示,χ²=21.04,p值﹤0.01,提示不同治疗方法其疗效不同,三组治疗有效率差异具有统计学意义。Cramer v = 0.20,疗法与治疗效果之间存在弱相关性。
3) 卡方分割多重比较
当卡方检验整体有显著性后,【实验/医学研究】→【卡方检验】模块会根据分组情况自动实现卡方分割法多重比较,本例结果如表 4-34示。
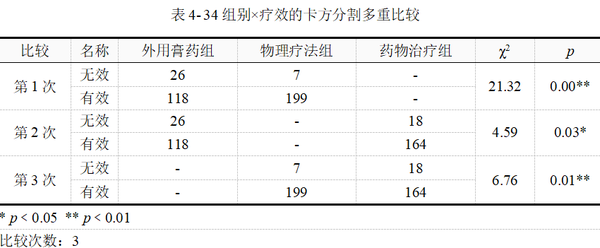
由上表可知,共进行3次拆分。第一次是外用膏药组与物理疗法组之间的治疗有效率差异比较;第2次是外用膏药组与药物治疗组之间的比较;第3次是物理疗法组与药物治疗组之间的比较。每一次拆分,都是一个独立的四格表卡方检验,输出对应的卡方统计量与显著性p值。
此处要注意到,表中最后一列的p值需要与校正后的显著性水平进行比较。本例进行3次两两比较,因此校正的显著性水平为α=0.05/3=0.0167,p值需与0.0167进行比较,从而推断检验的结果。
物理疗法组与外用膏药组p值﹤0.0167;物理疗法组与药物治疗组p值=0.01﹤0.0167。可以认为物理疗法与药物治疗、外用膏药的有效率均有统计学差异,具体来说是物理疗法的有效率高于其他两种疗法,但我们尚不能认为药物治疗与外用膏药的有效率有差异(p =0.03﹥0.0167)。
以上内容摘自《SPSSAU科研数据分析方法与应用》第4章——差异关系研究,书中不仅涵盖了数据清理、统计分析和模型构建等内容,还提供了丰富的案例,以便于读者在实际研究中应用。