STK与MATLAB互联——仿真导航卫星与地面用户间距离和仰角参数

news2024/11/29 2:28:12

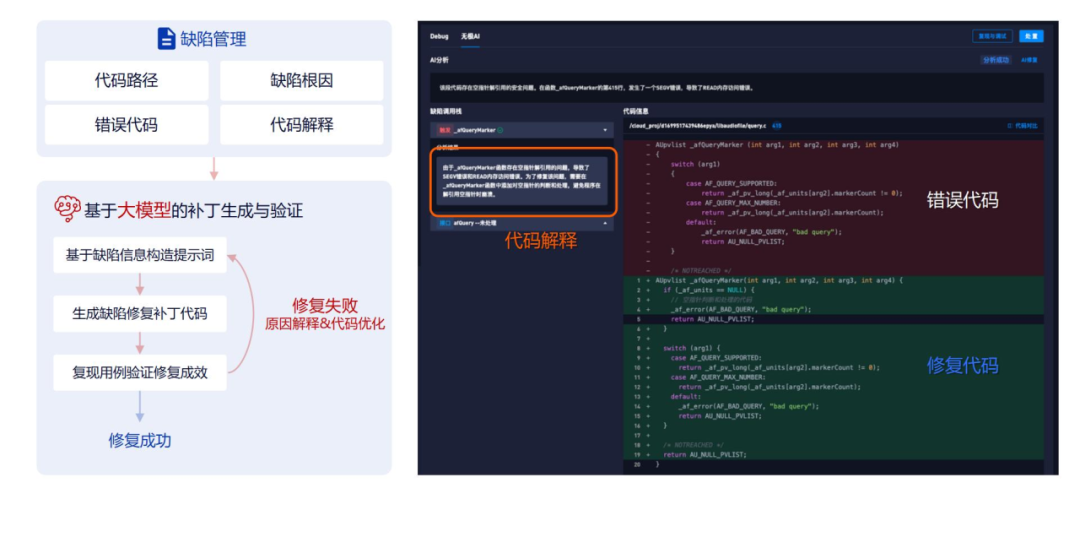
文章目录

    • 构建GPS星座
      • 创建单个PRN的GPS卫星
      • 创建GPS星座，并为其添加发射机
    • 北斗星座构建
    • 搭建低轨铱星星座
    • 构建一颗轨道高度为800km/1000km/1200km的低轨卫星
    • 构建一颗轨道高度为800km/1000km/1200km的低轨卫星
    • 建立地面站，可见性分析
      • 确定地面站坐标
      • 分析单颗卫星的可见性数据
      • 多颗卫星可见性数据分析
    • 结果分析
      • 最终版完整程序
      • 程序运行的注意事项
      • 数据的存储格式

本次仿真主要包括以下几个方面：

  • 使用MATLAB控制STK，构建GPS星座
  • 使用MATLAB控制STK，构建北斗星座
  • 使用MATLAB控制STK，分别构建一颗轨道高度为800km/1000km/1200km的低轨卫星，并将卫星的初始相位分别设为0、60、120、180度
  • 使用MATLAB控制STK，构建铱星星座
  • 使用MATLAB构建半径约550km的圆形区域，区域边界等距离地分布41个观测站
  • 创建卫星与观测站之间的连接
  • 计算导航卫星与地面用户之间的实时距离和仰角，并保存到MATLAB结构体中

+++

构建GPS星座

写程序之初，确实无法下手，因为在STK软件上简单点四下的东西（备注：分别点"Insert"-“New”-“Satellite”-“Load GPS Constellation"即可创建完整的GPS星座），放到MATLAB上就麻烦了许多。由于在matlab里，暂时不知道如何"Load GPS Constellation”，因此，选择了较笨的方法，一个PRN一个PRN地创建GPS卫星。

创建单个PRN的GPS卫星

要想构建一个星座，需要先分析单个PRN的GPS卫星如何创建。

首先，创建一个卫星，例如PRN3，这是创建卫星的通用的代码

sat = sc.Children.New(18,'mysatPRN3');

然后，我们可以在命令行窗口输入"sat."，再按一下Tab键，可以神奇的发现，居然会有很多参数，你可以看得到！像这样：（这里：请输入sat. ，不要像我一样输入sat(3).，因为我后面把sat赋予了32个不同的PRN因此，加了括号）

image-20220703205638319

接着，我们选择我们需要的参数，按回车键，这里因为需要设置卫星的类型，所以找到“SetPropagatorType”，按回车键。然后在AGI官方的使用说明中，搜索“SetPropagatorType”，找到设置为GPS类型的参数，然后写如下代码：

image-20220703205959168

sat.SetPropagatorType('ePropagatorGPS');

莫小看这一行代码，这一行就花了我2个小时时间才整明白咋回事。

然后，我们先写上这行代码

sat.Propagator.Propagate;

这样一个GPS卫星就定义好了，我们可以查看一下具体参数

image-20220703210447969

但问题来了，无论你生成多少颗GPS卫星，它的PRN都是01，那怎么办呢？

于是，在命令行，输入“sat.”，按Tab键，这次，我们选择 sat.Propagator，设置卫星的参数，然而发现，如果输入“ sat.Propagator.”的话，后面就不会再提示参数了，因此，我又想到了一个办法，先令“sat1=sat.Propagator；”然后，在命令行中输入“ sat1.”，这次，我们就看到了这样的几个可选参数：

image-20220703211416477

然后，选择PRN这一项，令

sat1.PRN=3

这样就实现了修改PRN的目标。

创建GPS星座，并为其添加发射机

添加循环，以创建GPS星座，代码如下：

%% 构建GPS星座
for PRN=[1 2 3 5 6 7 8 9 10 11 12 13 14 15 16 17 ...
        18 19 20 21 22 23 24 25 26 27 28 29 30 31 32]
    sat = sc.Children.New(18,['mysat',num2str(PRN)]);
    %sat.SetPropagatorType('ePropagatorGPS')
    sat.SetPropagatorType('ePropagatorGPS');
    sat.Propagator.PRN=PRN;
    sat.Propagator.Propagate;
end

点索引后面的参数，按Tab键是可以通过点索引找到对应的内容！！

image-20200703150732614

为每一个GPS卫星添加一个发射机，代码如下：

Transmitter = sat(PRN).Children.New('eTransmitter', 'Mytransmitter');
Transmitter.SetModel('GPS Satellite Transmitter Model');

还是之前的方法，输入“Transmitter.”，按Tab键，找到SetModel这个元素，按回车键，然后在AGI官方教程中找到合适的参数“GPS Satellite Transmitter Model”，即可修改发射机的类型。最终的程序代码如下：

clear all
clc
app = actxserver('STK11.application');
root = app.Personality2;
scenario = root.Children.New('eScenario','MATLAB_PredatorMission');
root.SaveScenarioAs('E:\Program Files\STK\Documents\STK 11 (x64)\Scenario1_jz2');
scenario.SetTimePeriod('2 Jun 2022 16:00:00.000','3 Jun 2022 16:00:00.000');
scenario.StartTime = '2 Jun 2022 16:00:00.000';
scenario.StopTime = '3 Jun 2022 16:00:00.000';
root.ExecuteCommand('Animate * Reset');
sc = root.CurrentScenario;

%% 构建GPS星座
for PRN=[1 2 3 5 6 7 8 9 10 11 12 13 14 15 16 17 ...
        18 19 20 21 22 23 24 25 26 27 28 29 30 31 32]
    sat(PRN) = sc.Children.New(18,['mysat',num2str(PRN)]);
    sat(PRN).SetPropagatorType('ePropagatorGPS')
    sat(PRN).Propagator.PRN=PRN;
    sat(PRN).Propagator.Propagate;
    %sensor = sat.Children.New('eSensor','MySensor_sat');
    Transmitter = sat(PRN).Children.New('eTransmitter', 'Mytransmitter');
    Transmitter.SetModel('GPS Satellite Transmitter Model');
end

北斗星座构建

在STK中，无法像GPS那样直接给卫星更改模型，所以使用了ssc number卫星标识号，在STK卫星库中找到北斗卫星并建立模型。

注：ssc number：美国国家航空和宇宙航行局网站给全球卫星进行的编号

从beidou3开始的卫星编号分别为

Num=[36287 36590 36828 37210 37256 37384 37763 37948 38091 38250 38251 38774 38775 38953 41434 43001 43002 43107 43108 43207 43208 43245 43246 43539 43581 43582 43602 43603 43622 43623 43647 43648 43683 43706 73707]

由于北斗1和北斗2被弃用，因此星座从北斗第三颗卫星开始，我们给出的编号也从第三颗卫星开始

sat = sc.Children.New(18,['mysatBD',num2str(i)]);

与前文使用相同的方法，我们可以设置卫星的类型和SSCNumber，并且将“AutoUpdateEnabled”置为1.

	sat.SetPropagatorType('ePropagatorSGP4');
    sat.Propagator.Segments.SSCNumber=num2str(Num);
    sat.Propagator.AutoUpdateEnabled=1;
    sat.Propagator.Propagate;

这句话必须有，否则报错

sat.Propagator.AutoUpdateEnabled=1;

下面写出代码（接着上面GPS的完整代码）

i=3;
for Num=[36287 36590 36828 37210 37256 37384 37763 37948 38091 38250 38251 38774 38775 38953 41434 43001 43002 43107 43108 43207 43208 43245 43246 43539 43581 43582 43602 43603 43622 43623 43647 43648 43683 43706 73707]
    sat = sc.Children.New(18,['mysatBD',num2str(i)]);
    i=i+1;
    sat.SetPropagatorType('ePropagatorSGP4');
    sat.Propagator.Segments.SSCNumber=num2str(Num);
    sat.Propagator.AutoUpdateEnabled=1;
    sat.Propagator.Propagate;
end
image-20220703160837604

搭建低轨铱星星座

关于手动搭建的方法，可以参考CSDN博客（十一）STK 中搭建铱星星座_清潇和梨花的博客，这里不做赘述，使用MATLAB控制STK建立的方法与北斗星座的建立相同，程序代码如下，结果图如下：

IRIDIUM 卫星编号IRIDIUM 卫星SSC NumberIRIDIUM 卫星编号IRIDIUM 卫星SSC Number
1454325311942959
1434325812242957
1404325212842811
1484325510742960
1504325713242961
1534307812942958
1444324912742956
1494325013342955
1464325412542964
1424325613642962
1574325113942963
1344307515843571
1414307716043569
1374307615943578
1164307216343575
1354307016543572
1514307416643570
1204280515443574
11342803105/16443577
1384307110841924
1304307315543573
1314307915643576
1174280810241920
1684392411241925
1804392210441922
1234280411441923
1264280910341918
1674393110941919
1714392910641917
1214281215243479
1184280714743480
1724392711043481
1734392511141926
image-20220704174419655

运行视频如下，可以很直观的进行可见性分析。

<video id=“video” controls=""src=“https://pdswsj.oss-cn-beijing.aliyuncs.com/img/20220704_174700.mp4” preload=“none”>

构建一颗轨道高度为800km/1000km/1200km的低轨卫星

构建一颗轨道高度为800km/1000km/1200km的低轨卫星

使用MATLAB控制STK，分别构建一颗轨道高度为800km/1000km/1200km的低轨卫星，并将卫星的初始相位分别设为0、60、120、180度

不同高度，不同星下点距圆心的距离，生成的低轨卫星如下图：

image-20220704201923891

代码如下：

%% 构建一颗轨道高度为800km/1000km/1200km的低轨卫星
height=[800 1000 1200];
arg=85:98;
s=1;
for nn=1:length(height)
    for nnn=1:length(arg)
        sat(s) = scenario.Children.New(18,['mysat',num2str(s)]);
        kep = sat(s).Propagator.InitialState.Representation.ConvertTo('eOrbitStateClassical');
        kep.SizeShapeType = 'eSizeShapeAltitude';
        kep.LocationType = 'eLocationTrueAnomaly';
        kep.Orientation.AscNodeType = 'eAscNodeLAN';
        kep.SizeShape.PerigeeAltitude = height(nn);    % 距地面最小距离km
        kep.SizeShape.ApogeeAltitude = height(nn);     % 距地面最大距离km
        kep.Orientation.Inclination = 60;
        kep.Orientation.ArgOfPerigee = 0;
        kep.Orientation.AscNode.Value = arg(nnn);
        kep.Location.Value = 0;
        sat(s).Propagator.InitialState.Representation.Assign(kep);
        sat(s).Propagator.Propagate;
        transmitter = sat(s).Children.New('eTransmitter', 'Mytransmitter');
        transmitter.SetModel('Complex Transmitter Model');
        txModel = transmitter.Model;
        txModel.Frequency = 14; %GHz
        s=s+1;
    end
end

<video id=“video” controls=""src=“https://pdswsj.oss-cn-beijing.aliyuncs.com/img/20220704_202415.mp4” preload=“none”>

建立地面站，可见性分析

确定地面站坐标

过程待分析

%% 确定地面站坐标
x0=120;     % 圆心在东经120°
y0=40;      % 北纬40°
R=5;        % 半径5°
alpha=0:pi/20:2*pi;
x=R*cos(alpha)+x0;
y=R*sin(alpha)+y0;

%% 建立地面站
for ii=1:length(alpha)
%     for lon=0:9
%         if lon~=0 | Lat~=0
            facility = root.CurrentScenario.Children.New('eFacility', ['MyFacility',num2str(ii)]);
            facility.Position.AssignGeodetic(y(ii),x(ii),0) % Latitude, Longitude, Altitude
            % Set altitude to height of terrain
            facility.UseTerrain = true;
            % Set altitude to a distance above the ground
            facility.HeightAboveGround = .05; % km
            sensor = facility.Children.New('eSensor',['MySensor',num2str(ii)]);

分析单颗卫星的可见性数据

接上面的程序，过程，时间原因，待分析。

            senConstraints = sensor.AccessConstraints;
            altitude = senConstraints.AddConstraint('eCstrRange');%file:///E:/Program%20Files/AGI/STK%2011/Help/Programming/index.htm#DocX/STKObjects~IAgSensor.html?Highlight=sensor.AccessConstraints
            altitude.EnableMax = true;
            altitude.Max = 0;
            % 可算出来了，设置了sensor的Constraints中的Range参数，让他为0，这样sensor就不会是个圆锥型了
            % IAgAccessConstraintCollection Collection
            % 对于sensor常规参数的修改，参考网址是：file:///E:/Program%20Files/AGI/STK%2011/Help/Programming/index.htm#DocX/STKObjects~IAgAccessConstraintCollection.html?Highlight=eCstrLunarElevationAngle%20eCstrLighting
            %STK开发如果没有头绪，一个是查帮助，另一个就是用get、invoke查看相
            %关信息。所以，上get
            %         pattern1.ConeAngle = 85;
            receiver = sensor.Children.New('eReceiver', ['MyReceiver',num2str(ii)]);
            %设置地面站约束
            facConstraints = receiver.AccessConstraints;
            %设置最大距离约束
            rangeCstr = facConstraints.AddConstraint('eCstrRange');
            rangeCstr.EnableMax = 1;
            rangeCstr.Max = 2000;
            %设置仰角约束
            elevationCstr = facConstraints.AddConstraint('eCstrElevationAngle');
            elevationCstr.EnableMin = 1;
            elevationCstr.Min = 5;
            for nn=1:length(sat)
            sat2fac=sat(nn).GetAccessToObject(facility);
            sat2fac.ComputeAccess;
            %         aerDP = sat2fac.DataProviders.Item('AER Data').Group.Item('VVLH CBF').Exec(scenario.StartTime,scenario.StopTime,60);
            %         azimuth = cell2mat(aerDP.DataSets.GetDataSetByName('Range').GetValues);
            acc_interval = sat2fac.ComputedAccessIntervalTimes;
            %可见次数如下
            count=acc_interval.Count;
            %可见的弧段起始时间列表
            %acc_interval.ToArray(0,-1)
            %str、sto分别是第一个弧段的起始时间，是字符串类型。
            acc(nn).AER(ii).result(1,:)={'Time' 'azimuth' 'range'};
            sum=0;
            for i=0:count-1
                [str,sto] = acc_interval.GetInterval(i);
                %结合上篇博文，获取第一个可见弧段内的方位角
                aerDP = sat2fac.DataProviders.Item('AER Data').Group.Item('VVLH CBF').Exec(str,sto,10);
                azimuth = cell2mat(aerDP.DataSets.GetDataSetByName('Azimuth').GetValues);
                range = cell2mat(aerDP.DataSets.GetDataSetByName('Range').GetValues);
                time = aerDP.DataSets.GetDataSetByName('Time').GetValues;
                len=length(range);
                for j=1:len
                    acc(nn).AER(ii).result(j+1+sum,:)={time(j) azimuth(j) range(j)};
                end
                sum=sum+len;
            end
            end
%         end
%     end
end

image-20220703174647685

多颗卫星可见性数据分析

最终效果图

<video id=“video” controls=""src=“https://pdswsj.oss-cn-beijing.aliyuncs.com/img/20220703_181255.mp4” preload=“none”>

结果分析

我们将access计算的结果存入了MATLAB的结构体中，方便之后随时调用，这里说明一下程序运行的注意事项和数据的存储格式。

最终版完整程序

clear all
clc
%% 建立场景，定义基本信息
app = actxserver('STK11.application');
root = app.Personality2;
scenario = root.Children.New('eScenario','MATLAB_PredatorMission');
root.SaveScenarioAs('E:\Program Files\STK\Documents\STK 11 (x64)\Scenario1_jz2');
scenario.SetTimePeriod('2 Jun 2022 16:00:00.000','3 Jun 2022 16:00:00.000');
scenario.StartTime = '2 Jun 2022 16:00:00.000';
scenario.StopTime = '3 Jun 2022 16:00:00.000';
root.ExecuteCommand('Animate * Reset');
sc = root.CurrentScenario;

% %% 构建GPS星座
% PRN=[1 2 3 5 6 7 8 9 10 11 12 13 14 15 16 17 ...
%         18 19 20 21 22 23 24 25 26 27 28 29 30 31 32];
% for nn=1:length(PRN)
%     sat(nn) = sc.Children.New(18,['mysat',num2str(PRN(nn))]);
%     sat(nn).SetPropagatorType('ePropagatorGPS')
%     %sat(nn).SetPropagatorType('ePropagatorGPS');
%     sat(nn).Propagator.PRN=PRN(nn);
%     %root.ExecuteCommand(['SetState */Satellite/gpsSat2 GPS 7 UpdateMode FromFiles SourceFile "C:\STKUser\Databases\GPSAlmanacs\GPSAlmanac.al3" TimePeriod "1 Jul 2006 12:00:00.00" "1 Jul 2006 16:00:00.00" StepSize 30.0']);
%     sat(nn).Propagator.Propagate;
%     %sensor = sat.Children.New('eSensor','MySensor_sat');
%     Transmitter = sat(nn).Children.New('eTransmitter', 'Mytransmitter');
%     Transmitter.SetModel('GPS Satellite Transmitter Model');
% end

% %% 构建北斗星座
% i=3;
% Num=[36287 36590 36828 37210 37256 37384 37763 37948 38091 38250 38251
% 38774 38775 38953 41434 43001 43002 43107 43108 43207 43208 43245 43246 43539 43581 43582 43602 43603 43622 43623 43647 43648 43683 43706 73707];
% for nn=1:length(Num)
%     sat(nn) = sc.Children.New(18,['mysatBD',num2str(i)]);
%     i=i+1;
%     sat(nn).SetPropagatorType('ePropagatorSGP4');
%     sat(nn).Propagator.Segments.SSCNumber=num2str(Num(nn));
%     sat(nn).Propagator.AutoUpdateEnabled=1;
%     sat(nn).Propagator.Propagate;
%     transmitter = sat(nn).Children.New('eTransmitter', 'Mytransmitter');
%     transmitter.SetModel('Complex Transmitter Model');
%     txModel = transmitter.Model;
%     txModel.Frequency = 1.26852; %GHz
% end

% %% 构建铱星星座
% i=1;
% IRIDIUM_num=[145 143 140 148 150 153 144 149 146 142 157 134 141 137 116 135 151 120 113 138 130 131 117 168 180 123 126 167 171 121 118 172 173 119 122 128 107 132 129 127 133 125 136 139 158 160 159 163 165 166 154 164  108 155 156 102 112 104 114 103 109 106 152 147 110 111];
% Num=[43253 43258 43252 43255 43257 43078 43249 43250 43254 43256 43251 43075 43077 43076 43072 43070 43074 42805 42803 43071 43073 43079 42808 43924 43922 42804 42809 43931 43929 42812 42807 43927 43925 42959 42957 42811 42960 42961 42958 42956 42955 42964 42962 42963 43571 43569 43578 43575 43572 43570 43574 43577 41924 43573 43576 41920 41925 41922 41923 41918 41919 41917 43479 43480 43481 41926 ];
% for nn=1:66
%     sat(nn) = sc.Children.New(18,['mysatIRIDIUM_num',num2str(IRIDIUM_num(i))]);
%     i=i+1;
%     sat(nn).SetPropagatorType('ePropagatorSGP4');
%     sat(nn).Propagator.Segments.SSCNumber=num2str(Num(nn));
%     sat(nn).Propagator.AutoUpdateEnabled=1;
%     sat(nn).Propagator.Propagate;
%     transmitter = sat(nn).Children.New('eTransmitter', 'Mytransmitter');
%     transmitter.SetModel('Complex Transmitter Model');
%     txModel = transmitter.Model;
%     txModel.Frequency = 14; %GHz
% end

%% 构建一颗轨道高度为800km/1000km/1200km的低轨卫星
height=[800 1000 1200];
arg=85:98;
s=1;
for nn=1:length(height)
    for nnn=1:length(arg)
        sat(s) = scenario.Children.New(18,['mysat',num2str(s)]);
        kep = sat(s).Propagator.InitialState.Representation.ConvertTo('eOrbitStateClassical');
        kep.SizeShapeType = 'eSizeShapeAltitude';
        kep.LocationType = 'eLocationTrueAnomaly';
        kep.Orientation.AscNodeType = 'eAscNodeLAN';
        kep.SizeShape.PerigeeAltitude = height(nn);    % 距地面最小距离km
        kep.SizeShape.ApogeeAltitude = height(nn);     % 距地面最大距离km
        kep.Orientation.Inclination = 60;
        kep.Orientation.ArgOfPerigee = 0;
        kep.Orientation.AscNode.Value = arg(nnn);
        kep.Location.Value = 0;
        sat(s).Propagator.InitialState.Representation.Assign(kep);
        sat(s).Propagator.Propagate;
        transmitter = sat(s).Children.New('eTransmitter', 'Mytransmitter');
        transmitter.SetModel('Complex Transmitter Model');
        txModel = transmitter.Model;
        txModel.Frequency = 14; %GHz
        s=s+1;
    end
end
%% 确定地面站坐标
x0=120;     % 圆心在东经120°
y0=40;      % 北纬40°
R=5;        % 半径5°
alpha=0:pi/20:2*pi;
x=R*cos(alpha)+x0;
y=R*sin(alpha)+y0;

%% 建立地面站
for ii=1:length(alpha)
%     for lon=0:9
%         if lon~=0 | Lat~=0
            facility = root.CurrentScenario.Children.New('eFacility', ['MyFacility',num2str(ii)]);
            facility.Position.AssignGeodetic(y(ii),x(ii),0) % Latitude, Longitude, Altitude
            % Set altitude to height of terrain
            facility.UseTerrain = true;
            % Set altitude to a distance above the ground
            facility.HeightAboveGround = .05; % km
            sensor = facility.Children.New('eSensor',['MySensor',num2str(ii)]);
            %         pattern1 = sensor.Pattern;
            %         sensor.FieldOfView
            
            %% 可见性分析
            senConstraints = sensor.AccessConstraints;
            altitude = senConstraints.AddConstraint('eCstrRange');%file:///E:/Program%20Files/AGI/STK%2011/Help/Programming/index.htm#DocX/STKObjects~IAgSensor.html?Highlight=sensor.AccessConstraints
            altitude.EnableMax = true;
            altitude.Max = 0;
            % 可算出来了，设置了sensor的Constraints中的Range参数，让他为0，这样sensor就不会是个圆锥型了
            % IAgAccessConstraintCollection Collection
            % 对于sensor常规参数的修改，参考网址是：file:///E:/Program%20Files/AGI/STK%2011/Help/Programming/index.htm#DocX/STKObjects~IAgAccessConstraintCollection.html?Highlight=eCstrLunarElevationAngle%20eCstrLighting
            %STK开发如果没有头绪，一个是查帮助，另一个就是用get、invoke查看相
            %关信息。所以，上get
            %         pattern1.ConeAngle = 85;
            receiver = sensor.Children.New('eReceiver', ['MyReceiver',num2str(ii)]);
            %设置地面站约束
            facConstraints = receiver.AccessConstraints;
            %设置最大距离约束
            rangeCstr = facConstraints.AddConstraint('eCstrRange');
            rangeCstr.EnableMax = 1;
            rangeCstr.Max = 2000;
            %设置仰角约束
            elevationCstr = facConstraints.AddConstraint('eCstrElevationAngle');
            elevationCstr.EnableMin = 1;
            elevationCstr.Min = 5;
            for nn=1:length(sat)
            sat2fac=sat(nn).GetAccessToObject(facility);
            sat2fac.ComputeAccess;
            %         aerDP = sat2fac.DataProviders.Item('AER Data').Group.Item('VVLH CBF').Exec(scenario.StartTime,scenario.StopTime,60);
            %         azimuth = cell2mat(aerDP.DataSets.GetDataSetByName('Range').GetValues);
            acc_interval = sat2fac.ComputedAccessIntervalTimes;
            %可见次数如下
            count=acc_interval.Count;
            %可见的弧段起始时间列表
            %acc_interval.ToArray(0,-1)
            %str、sto分别是第一个弧段的起始时间，是字符串类型。
            acc(nn).AER(ii).result(1,:)={'Time' 'azimuth' 'range'};
            sum=0;
            for i=0:count-1
                [str,sto] = acc_interval.GetInterval(i);
                %结合上篇博文，获取第一个可见弧段内的方位角
                aerDP = sat2fac.DataProviders.Item('AER Data').Group.Item('VVLH CBF').Exec(str,sto,10);
                azimuth = cell2mat(aerDP.DataSets.GetDataSetByName('Azimuth').GetValues);
                range = cell2mat(aerDP.DataSets.GetDataSetByName('Range').GetValues);
                time = aerDP.DataSets.GetDataSetByName('Time').GetValues;
                len=length(range);
                for j=1:len
                    acc(nn).AER(ii).result(j+1+sum,:)={time(j) azimuth(j) range(j)};
                end
                sum=sum+len;
            end
            end
%         end
%     end
end

程序运行的注意事项

程序分为8大部分，分别是：

  1. 建立场景，定义基本信息
  2. 构建GPS星座
  3. 构建北斗星座
  4. 构建铱星星座
  5. 构建一颗轨道高度为800km/1000km/1200km的低轨卫星
  6. 确定地面站坐标
  7. 建立地面站
  8. 可见性分析

需要注意的是，每次只能从2、3、4、5这四种场景中选择一种场景，其他三个场景都要注释掉！！！其他地方无需修改。

数据的存储格式

可见性分析的数据都存在了acc这个结构体字段中，每个字段包含了一颗卫星对所有观测站的数据结果，即这颗卫星与这41个地面测站之间的距离和仰角信息。

image-20220704221321568

卫星字段的存储顺序如下：

GPS星座的存储顺序是按照PRN的顺序，即：PRN=[1 2 3 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32]（注意没有PRN4）

北斗星座的存储顺序是按照PRN的顺序，即：3~37

铱星星座的存储顺序是：IRIDIUM_num=[145 143 140 148 150 153 144 149 146 142 157 134 141 137 116 135 151 120 113 138 130 131 117 168 180 123 126 167 171 121 118 172 173 119 122 128 107 132 129 127 133 125 136 139 158 160 159 163 165 166 154 164 108 155 156 102 112 104 114 103 109 106 152 147 110 111];

自定义轨道高度为800km/1000km/1200km的低轨卫星的顺序，可以读程序知：

height=[800 1000 1200];	% 轨道高度
arg=85:98;				% 初始轨道相位85°~98°之间
s=1;
for nn=1:length(height)
    for nnn=1:length(arg)
    	......
    end
end

点击acc结构体，acc(1).AER包含了PRN1卫星到每个观测站的可见性计算数据，一共有41个字段（因为有41个观测站）。

image-20220704222513276

点击其中一个，可以看到acc(1).AER(1).result的数据，包含了时刻信息，仰角和距离。

image-20220704222810407

注：这里不涉及到多普勒频率的计算问题，因此本文中的transmitter和receiver可以不加，单纯添加卫星和观测站即可。

（完）

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2227380.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Excel菜单选项无法点击？两种原因及解决方法全解析

Excel菜单选项无法点击？两种原因及解决方法全解析

在使用Excel处理数据时&#xff0c;有时会遇到菜单选项无法点击的情况。这种问题会影响到正常的操作和编辑。出现这种情况的原因可能有多种&#xff0c;本文将介绍两种常见的原因&#xff0c;并提供相应的解决方法&#xff0c;帮助小伙伴们快速恢复菜单选项的正常使用。 原因一…
阅读更多...
【银河麒麟高级服务器操作系统·实例分享】裸金属服务器开机失败分析及处理建议

【银河麒麟高级服务器操作系统·实例分享】裸金属服务器开机失败分析及处理建议

了解更多银河麒麟操作系统全新产品&#xff0c;请点击访问 麒麟软件产品专区&#xff1a;https://product.kylinos.cn 开发者专区&#xff1a;https://developer.kylinos.cn 文档中心&#xff1a;https://documentkylinos.cn 现象描述 裸金属物理服务器开机卡在EFI stub页面…
阅读更多...
基于Spring Boot的在线摄影工作室开发指南

基于Spring Boot的在线摄影工作室开发指南

1系统概述 1.1 研究背景 随着计算机技术的发展以及计算机网络的逐渐普及&#xff0c;互联网成为人们查找信息的重要场所&#xff0c;二十一世纪是信息的时代&#xff0c;所以信息的管理显得特别重要。因此&#xff0c;使用计算机来管理网上摄影工作室的相关信息成为必然。开发合…
阅读更多...
UE5蓝图中整理节点的方法

UE5蓝图中整理节点的方法

UE5蓝图中整理节点的方法 第一种&#xff1a;子图 右键选中的节点&#xff0c;出现一个面板&#xff0c;点击 Collapse Nodes 既可折叠选中的所有节点 注意&#xff1a;子图不可以被复制使用。 双击子图可以查看节点&#xff0c;若不想折叠选中的节点为子图&#xff0c;右键点…
阅读更多...
喜讯丨江苏省医药行业协会·中药饮片专业委员会2024年度三届五次会员代表大会暨《江苏中药饮片》通讯员年度表彰大会圆满举行

喜讯丨江苏省医药行业协会·中药饮片专业委员会2024年度三届五次会员代表大会暨《江苏中药饮片》通讯员年度表彰大会圆满举行

2024年10月25日&#xff0c;江苏省医药行业协会中药饮片专业委员会三届五次&#xff08;2024年度&#xff09;会员代表大会暨《江苏中药饮片》通讯员年度表彰大会在苏州香格里拉大酒店隆重召开。 江苏省药品监督管理局、药品生产监管局、江苏省医药行业协会、江苏省食品药品监督…
阅读更多...
git push到远程怎么回退

git push到远程怎么回退

git push到远程服务器想继续修改&#xff0c;你必须要回退然后在此提交。而且需要保留本地的修改文件。 下面给你一些git命令&#xff0c;回退很简单。 按照下面的流程操作就行&#xff1a; 1.查看提交历史 首先&#xff0c;使用git log命令查看提交历史。可以使用以下命令显…
阅读更多...
回溯法 | 无限个for循环？

回溯法 | 无限个for循环？

文章目录 起因实现 优化 起因 回溯算法&#xff0c;寻找问题的所有解或最优解 最开始遇到这样一个问题&#xff0c;认为可以用几个for循环暴力解决&#xff0c;然而仔细观察后发现&#xff0c;针对不同的输入&#xff0c;我需要的for循环的个数不一样&#xff0c;只能使用递归…
阅读更多...
react18中react-thunk实现公共数据仓库的异步操作

react18中react-thunk实现公共数据仓库的异步操作

redux及react-redux都只能实现数据的同步修改更新&#xff0c;有点类似于vue中的mutation&#xff0c;只能做同步操作&#xff0c;异步的话不用actions来实现。由于在项目始终不可避免要实现的异步数据的更新&#xff0c;这明显不够用了。是时候引入我们的异步中间件redux-thun…
阅读更多...
原生js实现拖拽上传（拖拽时高亮上传区域）

原生js实现拖拽上传（拖拽时高亮上传区域）

文章目录 drop相关事件说明-MDN演示代码&#xff08;.html) drop相关事件说明-MDN 演示 代码&#xff08;.html) <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"…
阅读更多...
最新XL换脸术！EcomID，更像更强，结合InstantID和PuLID优点，200万训练集，6.6显存占用，ComfyUI

最新XL换脸术！EcomID，更像更强，结合InstantID和PuLID优点，200万训练集，6.6显存占用，ComfyUI

由阿里妈妈最新开源的换脸工具&#xff1a;EcomID&#xff0c;结合了InstantID和PuLID优点&#xff0c;以获得更好的背景一致性、面部关键点控制、更真实的面部以及更高的相似度。旨在从单个ID参考图像生成定制的保ID图像&#xff0c;优势在于很强的语义一致性&#xff0c;同时…
阅读更多...
情感咨询小程序的市场需求大吗？

情感咨询小程序的市场需求大吗？

情感咨询小程序的市场需求较大&#xff0c;主要体现在以下几个方面&#xff1a; 情感问题普遍存在5&#xff1a; 恋爱关系困扰&#xff1a;在恋爱过程中&#xff0c;人们经常会遇到诸如沟通不畅、争吵频繁、信任危机等问题。例如&#xff0c;年轻人在恋爱初期可能会因为不了解…
阅读更多...
技术分享 | 大语言模型增强灰盒模糊测试技术探索

技术分享 | 大语言模型增强灰盒模糊测试技术探索

大语言模型凭借其庞大的参数规模&#xff0c;能够通过无监督学习从海量文本中获取知识&#xff0c;从而不仅能够深刻理解文本语义&#xff0c;还能准确识别文本的格式和结构。凭借对不同数据结构的深度理解&#xff0c;大语言模型已在众多领域得到广泛应用。其中&#xff0c;尤…
阅读更多...
Cmake Error:could not find any instance of Visual Studio.

Cmake Error:could not find any instance of Visual Studio.

出现以下错误 解决方案&#xff1a; 安装visual stuido 2017。 检查是否安装“使用C的桌面开发” 检查是否安装了扩展开发 点开“单个组件”是否安装了以下组件 编辑计算机环境变量&#xff0c;
阅读更多...
linux查看文件命令

linux查看文件命令

查看文件命令 显示命令 cat 语法&#xff1a;cat 【选项】 文件 选项 命令含义n显示行号包括空行b显示行号不包括空行s压缩空行为一行A显示隐藏字符 cat -n 文件&#xff1a;显示行号包括空行 cat -b 文件 cat -s 文件 cat -A 文件 more和less是 分页查看 tac和rev都…
阅读更多...
使用Python统计目录下所有.txt文件中的字符数

使用Python统计目录下所有.txt文件中的字符数

前言 在日常开发或数据处理中&#xff0c;我们经常需要对大量文本文件进行各种统计操作&#xff0c;比如计算总字数。本文将介绍一种简单的方法&#xff0c;通过Python脚本遍历指定目录下的所有.txt文件&#xff0c;并统计这些文件中的字符总数。这个过程可以帮助开发者更好地…
阅读更多...
【Kaggle | Pandas】练习2：索引，选择和分配

【Kaggle | Pandas】练习2：索引，选择和分配

文章目录 数据总表1、读取列2、读取某列的第几行的值3、第一行数据4、读取列中前10个值5、读取索引标签为1 、 2 、 3 、 5和8的记录6、包含索引标签为0 、1 、10和100的记录的country 、province 、 region_1和region_2列7、 前 100 条记录的country和variety列8、包含Italy葡…
阅读更多...
三款计算服务器配置→如何选择科学计算服务器？

三款计算服务器配置→如何选择科学计算服务器？

科学计算在众多领域都扮演着关键角色&#xff0c;无论是基础科学研究还是实际工程应用&#xff0c;强大的计算能力都是不可或缺的。而选择一台合适的科学计算服务器&#xff0c;对于确保科研和工作的顺利进行至关重要。 首先&#xff0c;明确自身需求是重中之重。要仔细考虑计算…
阅读更多...
【ceral】c++轻量的序列化库

【ceral】c++轻量的序列化库

背景 在开发硬件产品时&#xff0c;会有一些参数配置文件&#xff0c;为了保密性或者传输&#xff0c;需要对其序列化处理&#xff0c;待到产品读取文件时&#xff0c;进行反序列化解码转化为设定的参数类型。 简介 ceral是一个仅包含头文件的C序列化库&#xff0c;可以将任…
阅读更多...
前后端请求、返回数据的多种方式

前后端请求、返回数据的多种方式

Springboot项目的业务逻辑 &#x1f319;项目基本结构&#xff1a; 通常情况下&#xff0c;我们在搭建后端项目的时候&#xff0c;处理业务逻辑我们需要用到Controller,Service,Mapper(mybatis,mybatis-plus)&#xff0c;Entry各层之间的相互调用来完成&#xff0c;还有就是我…
阅读更多...
计算机网络-MSTP的基础概念

计算机网络-MSTP的基础概念

前面我们大致了解了MSTP的由来&#xff0c;是为了解决STP/RSTP只有一根生成树导致的VLAN流量负载分担与次优路径问题&#xff0c;了解MSTP采用实例映射VLAN的方式实现多实例生成树&#xff0c;MSTP有很多的理论概念需要知道&#xff0c;其实与其它的知识一样理论复杂配置还好的…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023