python机器人编程——一种3D骨架动画逆解算法的启示（上）

news2024/11/30 2:25:58

目录

  • 一、前言
  • 二、fabrik 算法
  • 三、python实现
  • 结论
  • PS.扩展阅读
    • ps1.六自由度机器人相关文章资源
    • ps2.四轴机器相关文章资源
    • ps3.移动小车相关文章资源
    • ps3.wifi小车控制相关文章资源

一、前言

我们用blender等3D动画软件时，会用到骨骼的动画，通过逆向IK动力学，可以实现控制少量点，就能控制一个复杂的骨架运动。这种IK动力学几乎是实时的，非常的高效。这种IK动力学算法的代表是fabrik 算法，该算法应被用于UE虚幻引擎、Unity等3D软件中。大至效果是，可以实现骨架的目标跟随，而且几乎是“实时”的：
在这里插入图片描述
这种感觉，不就是机械臂的虚拟拖拽吗？是否可以给机械臂的逆解，或者是虚拟化示教带来一些启发，是一个有意思的应用。本篇先来初步研究一下fabrik 算法。

二、fabrik 算法

该算法在文章 FABRIK: A fast, iterative solver for the Inverse Kinematics problem中有详细说明，FABRIK算法是一种用于解决逆运动学问题的启发式方法。它通过迭代地调整关节链，使末端执行器逐渐接近目标位置。与传统方法相比，FABRIK算法不需要使用旋转角度或矩阵，而是通过在线段上定位点来找到每个关节的位置，这使得它在计算上更加高效，并且能够产生视觉上现实的关节姿势。
在这里插入图片描述

三、python实现

网上已经有很多实现的python算法，这里，主要是利用实现的3D算法，实现在matplot中的IK，即，任意点击3D坐标点，实现IK，骨架的末端移动到目标点，就像开始的blender一样。
在这里插入图片描述
首先，我们需要导入一些必要的Python库，包括NumPy、Math、Matplotlib等，用于数学运算和图形绘制。

import numpy as np
import math
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
import re

单位向量函数
定义了一个函数 unitVector，它接受一个向量作为输入，并返回该向量的单位向量。

def unitVector(vector):
    return vector / np.linalg.norm(vector)

Segment3D 类用于存储逆运动学链的一部分。它接受参考点坐标、段长度和初始角度作为参数，并计算出该段的新坐标。

class Segment3D:
    def __init__(self, referenceX, referenceY, referenceZ, length, zAngle, yAngle):
        self.zAngle = zAngle
        self.yAngle = yAngle
        self.length = length
        deltaX = math.cos(math.radians(zAngle)) * length
        deltaY = math.sin(math.radians(zAngle)) * length
        deltaZ = math.sin(math.radians(yAngle)) * length
        newX = referenceX + deltaX
        newY = referenceY + deltaY
        newZ = referenceZ + deltaZ
        self.point = np.array([newX, newY, newZ])

FabrikSolver3D 类是FABRIK算法的核心，它初始化了一个3D逆运动学求解器，并提供了添加段、检查可达性、迭代求解和绘图等功能。

        
class FabrikSolver3D:
    """ 
        An inverse kinematics solver in 3D. Uses the Fabrik Algorithm.
    """
    def __init__(self, baseX=0, baseY=0, baseZ=0,  marginOfError=0.01):
        

        # Create the base of the chain.
        self.basePoint = np.array([baseX, baseY, baseZ])

        # Initialize empty segment array -> [].
        self.segments = []

        # Initialize length of the chain -> 0.
        self.armLength = 0

        # Initialize the margin of error.
        self.marginOfError = marginOfError
        self.targetpoint=None
        self.fig = plt.figure()
        self.ax1 = self.fig.add_subplot(111, projection="3d")
        self.mousep=None


    def addSegment(self, length, zAngle, yAngle):

        

        if len(self.segments) > 0:

            segment = Segment3D(self.segments[-1].point[0], self.segments[-1].point[1], self.segments[-1].point[2], length, zAngle + self.segments[-1].zAngle, self.segments[-1].yAngle + yAngle)
        else:
            # Maak een segment van de vector beginpoint, lengte en hoek.
            segment = Segment3D(self.basePoint[0], self.basePoint[1], self.basePoint[2], length, zAngle, yAngle)

        # Voeg lengte toe aan de totale armlengte.
        self.armLength += segment.length

        # Voeg de nieuwe segment toe aan de list.
        self.segments.append(segment)

    def isReachable(self, targetX, targetY, targetZ):
        

        if np.linalg.norm(self.basePoint - np.array([targetX, targetY, targetZ])) < self.armLength:
            return True
        return False

    def inMarginOfError(self, targetX, targetY, targetZ):
        
        if np.linalg.norm(self.segments[-1].point - np.array([targetX, targetY, targetZ])) < self.marginOfError:
            return True
        return False     

    def iterate(self, targetX, targetY, targetZ):
       
        target = np.array([targetX, targetY, targetZ])

        # Backwards.
        for i in range(len(self.segments) - 1, 0, -1):

            if i == len(self.segments) - 1:
              
                self.segments[i-1].point = (unitVector(self.segments[i-1].point - target) * self.segments[i].length) + target

            else:
                self.segments[i-1].point = (unitVector(self.segments[i-1].point - self.segments[i].point) * self.segments[i].length) + self.segments[i].point

         # Forwards.
        for i in range(len(self.segments)):
            if i == 0:
                self.segments[i].point = (unitVector(self.segments[i].point - self.basePoint) * self.segments[i].length) + self.basePoint

            elif i == len(self.segments) - 1:
                self.segments[i].point = (unitVector(self.segments[i-1].point - target) * self.segments[i].length * -1) + self.segments[i-1].point

            else:
                self.segments[i].point = (unitVector(self.segments[i].point - self.segments[i-1].point) * self.segments[i].length) + self.segments[i-1].point

    def compute(self, targetX, targetY, targetZ):

      
        
        if self.isReachable(targetX, targetY, targetZ):
            while not self.inMarginOfError(targetX, targetY, targetZ):
                self.iterate(targetX, targetY, targetZ)   
                self.targetpoint=[targetX, targetY, targetZ]
        else:
            print('Target not reachable.')
            sys.exit()

    def plot(self, save=False, name="graph"):
        
        self.ax1.clear()  # 清除当前轴
        ax1=self.ax1
        
        # Plot arm.
        for i, segment in enumerate(self.segments):
            #ax1.scatter(segment.point[2], segment.point[0], segment.point[1], c='b')
            ax1.scatter(segment.point[0], segment.point[1], segment.point[2], c='b')
            if i > 0:  # Connect to the previous segment
                ax1.plot([self.segments[i-1].point[0], segment.point[0]],
                          [self.segments[i-1].point[1], segment.point[1]],
                          [self.segments[i-1].point[2], segment.point[2]], 'b-')
                """
                ax1.plot([self.segments[i-1].point[2], segment.point[2]],
                          [self.segments[i-1].point[0], segment.point[0]],
                          [self.segments[i-1].point[1], segment.point[1]], 'b-')
                """
        # Connect the last segment to the base point
        """
        ax1.plot([self.basePoint[2], self.segments[0].point[2]],
                  [self.basePoint[0], self.segments[0].point[0]],
                  [self.basePoint[1], self.segments[0].point[1]], 'b-')
        """
        ax1.plot([self.basePoint[0], self.segments[0].point[0]],
                  [self.basePoint[1], self.segments[0].point[1]],
                  [self.basePoint[2], self.segments[0].point[2]], 'b-')
    
        # Start point
        #ax1.scatter(self.basePoint[2], self.basePoint[0], self.basePoint[1], c='g')
        ax1.scatter(self.basePoint[0], self.basePoint[1], self.basePoint[2], c='g')
        
        ax1.scatter(self.targetpoint[0],self.targetpoint[1],self.targetpoint[2], c='r',alpha=0.6, s=100)
        
                
        ax1.set_ylabel('y-axis')
        ax1.set_zlabel('z-axis')
        ax1.set_xlabel('x-axis')
        # Set the view angle so that the z-axis is pointing upwards
        ax1.view_init(elev=45., azim=45.)
        plt.pause(0.01)
    

    def extract_coordinates(self,s):
        # 使用正则表达式匹配x, y, z的值
        # 注意：负号前面加上了反斜杠进行转义
        # 使用正则表达式提取实数值，包括负号
        pattern = r'−?\d+\.\d+'
        matches = re.findall(pattern, s)
        values = [float(match.replace('−', '-')) for match in matches]
        x, y, z=values 
    
        return x, y, z
        
    def show(self):
        self.plot()
        self.fig.canvas.mpl_connect('button_press_event', self.on_click)  # 连接点击事件
        self.fig.canvas.mpl_connect('motion_notify_event', self.on_motion) 
        plt.show()
    def on_motion(self,event):
        if event.inaxes is not None:
            x, y = event.xdata, event.ydata
            sting = self.ax1.format_coord(x, y)              
            x,y,z=self.extract_coordinates(sting)
            #print(x,y,z) 
            self.mousep=(x,y,z)
    def on_click(self, event):
        # 检查点击事件是否在坐标轴内
        if event.inaxes is not None:
            print(f'Clicked on axis {event.inaxes}')
            # 触发你的函数
            print(self.mousep)
            if not type(self.mousep) == type(None):           
                x,y,z=self.mousep
                print("compute")
                self.compute(x, y, z)
                self.plot()
            # 获取点击的坐标值
            

            #self.compute(x, y, z)
            # 重绘图形
            #

可以通过如下步骤实现逆解：

  • 添加关节段：通过addSegment方法，我们可以为机械臂添加多个关节段，每个关节段都有自己的长度和初始角度。

  • 检查可达性：isReachable方法检查目标位置是否在机械臂的可达范围内。

  • 迭代计算：iterate方法执行一次FABRIK算法迭代，调整关节位置以接近目标。

  • 绘图显示：plot方法用于在3D空间中绘制机械臂的当前状态，show方法则显示最终的图形界面，并允许用户通过点击来选择目标位置。

  • 事件处理：on_click和on_motion方法用于处理用户的点击和鼠标移动事件，以便动态地调整目标位置。

        
        
if __name__ == "__main__":        
    arm = FabrikSolver3D()    
    arm.addSegment(0, 0, 0)
    arm.addSegment(50, 0, 0)
    arm.addSegment(50, 0, 0)
    arm.addSegment(50, 0, 0)
    arm.addSegment(50, 0, 0)
    arm.compute(50, 50, 100)    
    arm.show()

在这里插入图片描述

结论

通过这个Python实现，我们可以看到FABRIK算法在解决3D逆运动学问题中的强大能力。它不仅能够快速找到解决方案，还能够实时响应用户的交互，这在模拟和实际应用中都是非常有价值的。接下来我们尝试丰富这个算法，在各关节添加约束，并应用到6轴机械臂的IK计算中，看看能否获得预期效果。

[------------本篇完-------------]

PS.扩展阅读

————————————————————————————————————————

对于python机器人编程感兴趣的小伙伴，可以进入如下链接阅读相关咨询

ps1.六自由度机器人相关文章资源

(1) 对六自由度机械臂的运动控制及python实现（附源码)
在这里插入图片描述

(2) N轴机械臂的MDH正向建模，及python算法
在这里插入图片描述

ps2.四轴机器相关文章资源

(1) 文章：python机器人编程——用python实现一个写字机器人
在这里插入图片描述

在这里插入图片描述

（2）python机器人实战——0到1创建一个自动是色块机器人项目-CSDN直播

(3)博文《我从0开始搭建了一个色块自动抓取机器人，并实现了大模型的接入和语音控制-(上基础篇)》的vrep基础环境
(3)博文《我从0开始搭建了一个色块自动抓取机器人，并实现了大模型的接入和语音控制-(上基础篇)》的vrep基础环境
(4)实现了语音输入+大模型指令解析+机器视觉+机械臂流程打通
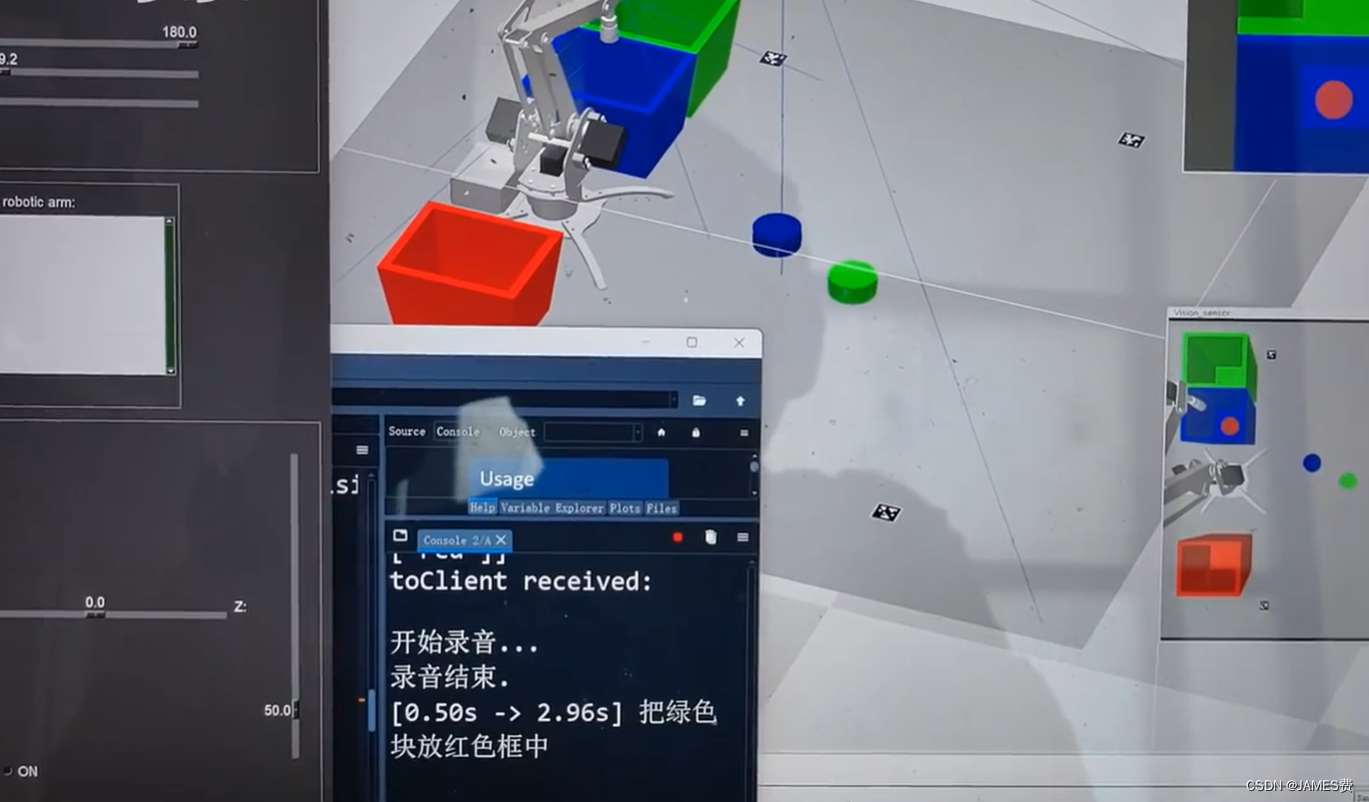
在这里插入图片描述
在这里插入图片描述

ps3.移动小车相关文章资源

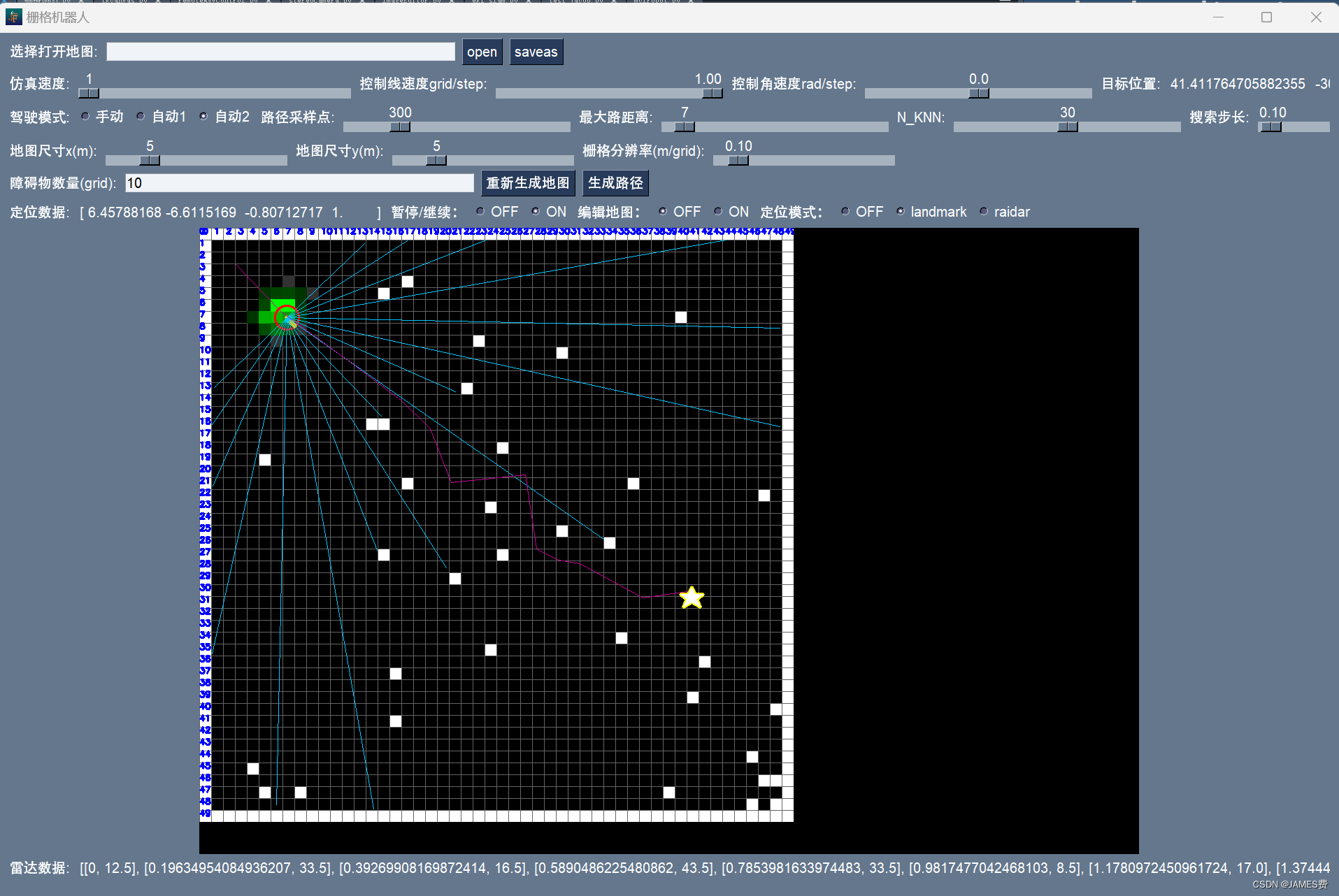
（1）python做了一个极简的栅格地图行走机器人，到底能干啥？[第五弹]——解锁蒙特卡洛定位功能-CSDN博客
(2) 对应python资源：源码地址
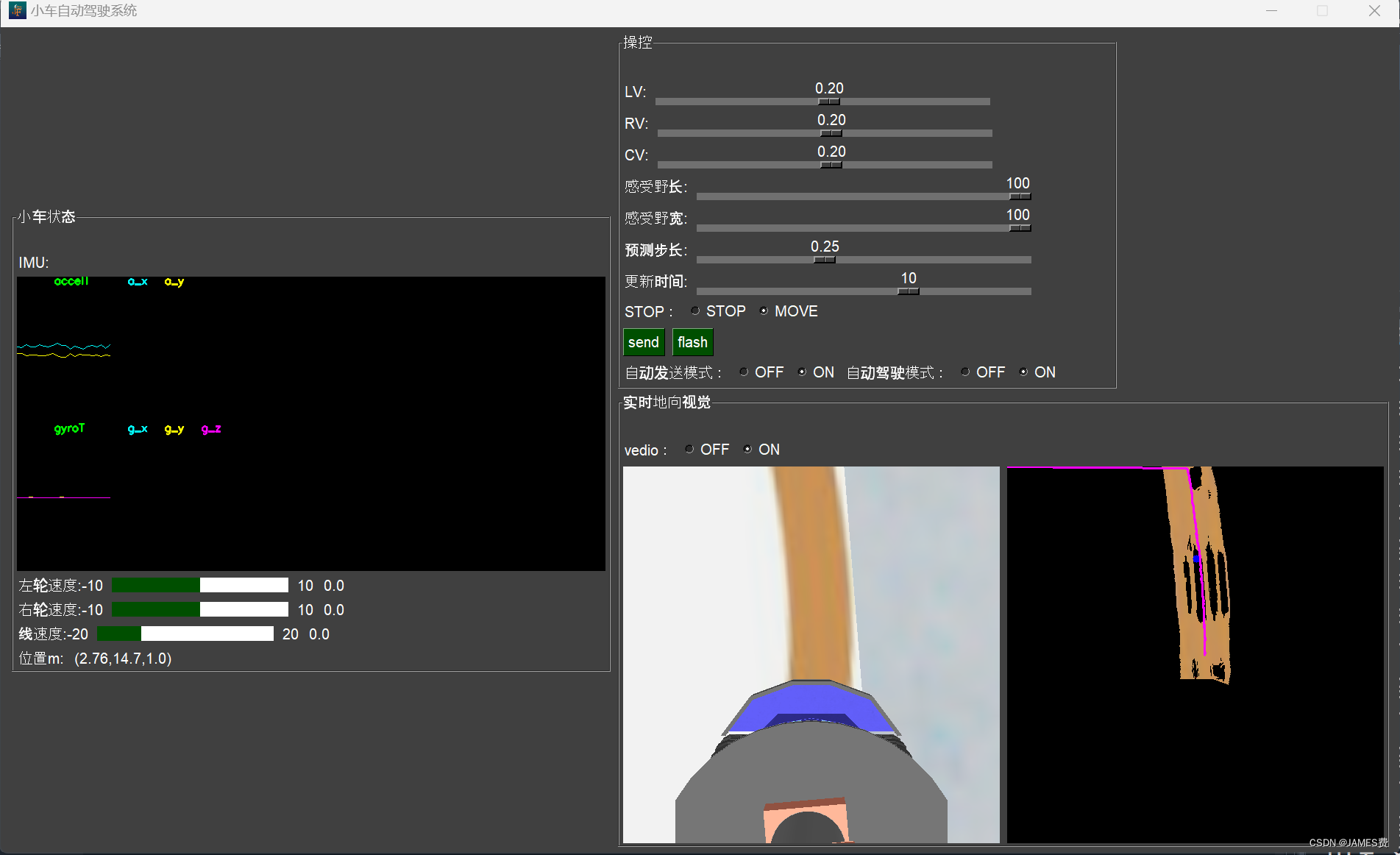
在这里插入图片描述
在这里插入图片描述

(3)python机器人编程——差速AGV机器、基于视觉和预测控制的循迹、自动行驶（上篇）_agv编程-CSDN博客
(4)python机器人编程——差速AGV机器、基于视觉和预测控制的循迹、自动行驶（下篇）_agv路线规划原则python-CSDN博客
对应python及仿真环境资源：源码链接
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

ps3.wifi小车控制相关文章资源

web端配套资源源代码已经上传(竖屏版)，下载地址
仿真配套资源已经上传：下载地址
web端配套资源源代码已经上传(横屏版)，下载地址

在这里插入代码片

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2227042.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

docker上传离线镜像包到Artifactory

docker上传离线镜像包到Artifactory

docker上传离线镜像包到Artifactory 原创 大阳 北京晓数神州科技有限公司 2024年10月25日 17:33 北京 随着docker官方源的封禁&#xff0c;最近国内资源也出现无法拉取的问题&#xff0c;Artifactory在生产环境中&#xff0c;很少挂外网代理去官方源拉取&#xff0c;小编提供…
阅读更多...
await前后线程切换改变，AsyncLocal＜T＞比ThreadLocal＜T＞ 更适合多线程变量隔离的场景

await前后线程切换改变，AsyncLocal＜T＞比ThreadLocal＜T＞ 更适合多线程变量隔离的场景

1. await前后线程发生切换&#xff0c;不一定保留在原线程中执行&#xff1b; 2. AsyncLocal<T> 比 ThreadLocal<T> 更适合多数多线程变量隔离的场景。 从 ThreadLocal 到 AsyncLocal https://cloud.tencent.cn/developer/article/1902826
阅读更多...
xss跨站及绕过与防护

xss跨站及绕过与防护

XSS 它主要是指攻击者可以在页面中插入恶意脚本代码&#xff0c;当受害者访问这些页面时&#xff0c;浏览器会解析并执行这些恶意代码&#xff0c;从而达到窃取用户身份/钓鱼/传播恶意代码等行为。 SVG-XSS SVG(Scalable Vector Graphics)是一种基于XML的二维矢量图格式&…
阅读更多...
WDG看门狗---独立看门狗和窗口看门狗

WDG看门狗---独立看门狗和窗口看门狗

目录 一. 前言 1. STM32内置看门狗 2. 看门狗的实质 二. 独立看门狗 1. 独立看门狗的系统框图 2. 键寄存器 3. IWDG的超时时间 三. 窗口看门狗 1. 窗口看门狗的系统框图 2. WWDG的工作特性 四. 独立看门狗和窗口看门狗的代码配置 1. 独立看门狗 2. 窗口看门狗 一. 前言 1. S…
阅读更多...
一篇文章讲透数据结构之二叉搜索树

一篇文章讲透数据结构之二叉搜索树

前言 在前面的学习过程中&#xff0c;我们已经学习了二叉树的相关知识。在这里我们再使用C来实现一些比较难的数据结构。 这篇文章用来实现二叉搜索树。 一.二叉搜索树 1.1二叉搜索树的定义 二叉搜索树&#xff08;Binary Search Tree&#xff09;是基于二叉树的一种升级版…
阅读更多...
python：ADB通过包名打开应用

python：ADB通过包名打开应用

一、依赖库 os 二、命令 1.这是查看设备中所有应用包名的最简单方法。只需在命令行中输入以下命令&#xff1a; adb shell pm list packages 2.打印启动的程序包名 adb shell am monitor回车&#xff0c;然后启动你想要获取包名的那个应用&#xff0c;即可获得 3.查看正在运…
阅读更多...
【AI开源项目】LangChain-3分钟让你知道什么是LangChain，以及LangChain的部署配置全流程

【AI开源项目】LangChain-3分钟让你知道什么是LangChain，以及LangChain的部署配置全流程

文章目录 什么是 LangChain&#xff1f;LangChain 概述主要特点 理解 Agent 和 ChainChainAgent示例简单顺序链示例 检索增强生成&#xff08;RAG&#xff09;LLM 面临的主要问题RAG 的工作流程 LangChain 核心组件1. 模型输入/输出&#xff08;Model I/O&#xff09;2. 数据连…
阅读更多...
CXL与近内存计算结合，会发生什么？--part1

CXL与近内存计算结合，会发生什么？--part1

一、基础背景 传统的冯诺依曼架构虽然广泛应用于各类计算系统&#xff0c;但其分离的数据存储与处理单元导致了数据传输瓶颈&#xff0c;特别是在处理内存密集型任务时&#xff0c;CPU或GPU需要频繁地从内存中读取数据进行运算&#xff0c;然后再将结果写回内存&#xff0c;这…
阅读更多...
React + Vite + TypeScript + React router项目搭建教程

React + Vite + TypeScript + React router项目搭建教程

一、创建项目 运行项目 二、目录结构 项目目录&#xff1a; ├─node_modules //第三方依赖 ├─public //静态资源&#xff08;不参与打包&#xff09; └─src├─assets //静态资源├─components //组件├─config //配置├─http //请求方法封装├─layout //页面…
阅读更多...
SCI一区级 | Matlab实现SSA-TCN-LSTM-Attention多变量时间序列预测

SCI一区级 | Matlab实现SSA-TCN-LSTM-Attention多变量时间序列预测

目录 效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.基于SSA-TCN-LSTM-Attention麻雀搜索算法优化时间卷积长短期记忆神经网络融合注意力机制多变量时间序列预测&#xff0c;要求Matlab2023版以上&#xff0c;自注意力机制&#xff0c;一键单头注意力机制替换成多头注…
阅读更多...
【Linux学习】（9）调试器gdb

【Linux学习】（9）调试器gdb

前言 Linux基础工具&#xff1a;安装软件我们用的是yum&#xff0c;写代码用的是vim&#xff0c;编译代码用gcc/g&#xff0c;调试代码用gdb&#xff0c;自动化构建用make/Makefile&#xff0c;多人协作上传代码到远端用的是git。 在前面我们把yum、vim、gcc、make、git都已经学…
阅读更多...
Linux系统下minio设置SSL证书进行HTTPS远程连接访问

Linux系统下minio设置SSL证书进行HTTPS远程连接访问

文章目录 1.配置SSL证书使用HTTPS访问2.MINIO SDK 忽略证书验证3.使用受信任的证书 1.配置SSL证书使用HTTPS访问 生成域名对应的SSL证书&#xff0c;下载Apache版本&#xff0c;我目前只发现Apache这个里面有对应的私钥和证书 私钥重命名为private.key证书重命名为public.crt&…
阅读更多...
Diffusion原理

Diffusion原理

Diffusion 文章目录 Diffusion前置知识基本介绍数学推导前向过程反向过程损失求解前置知识 马尔科夫链： 第 i i i时刻上的状态条件依赖于且仅依赖于第 i − 1 i-1 i−1时刻的状态条件，即 ​ P ( x i ∣ x i − 1 , x i − 2 , . . . , x 1 ) = P ( x i ∣ x i − 1 ) P(x…
阅读更多...
以通俗易懂的仓库来讲解JVM内存模型

以通俗易懂的仓库来讲解JVM内存模型

JVM内存模型可以想象成一个大型的仓库&#xff0c;这个仓库被分成了几个不同的区域&#xff0c;每个区域都有特定的用途和规则。下面我们用一个仓库的比喻来介绍JVM内存模型&#xff1a; 仓库大门&#xff08;JVM启动&#xff09;&#xff1a; 当JVM启动时&#xff0c;就像打开…
阅读更多...
排查PHP服务器CPU占用率高的问题

排查PHP服务器CPU占用率高的问题

排查PHP服务器CPU占用率高的问题通常可以通过以下步骤进行&#xff1a; 使用top或htop命令&#xff1a;这些命令可以实时显示服务器上各个进程的CPU和内存使用情况。找到CPU使用率高的进程。 查看进程日志&#xff1a;如果PHP-FPM或Apache等服务器进程的日志记录了具体的请求…
阅读更多...
Django入门教程——用户管理实现

Django入门教程——用户管理实现

第六章 用户管理实现 教学目的 复习数据的增删改查的实现。了解数据MD5加密算法以及实现模型表单中&#xff0c;自定义控件的使用中间件的原理和使用 需求分析 系统问题 员工档案涉及到员工的秘密&#xff0c;不能让任何人都可以看到&#xff0c;主要是人事部门进行数据的…
阅读更多...
su user更换用户后无法打开图形屏幕Cannot open your terminal ‘/dev/pts/0‘ 解决办法

su user更换用户后无法打开图形屏幕Cannot open your terminal ‘/dev/pts/0‘ 解决办法

我在docker内使用了su john更换了用户&#xff0c;执行petalinux-config -c kernel时打不开图形屏幕窗口&#xff0c;需要执行命令script /dev/null 进入docker和配置状态的所有命令行命令如下&#xff1a; johnjohn-hp:~/zynq$ ./docker_ubuntu16.sh rootjohn-hp:/home/john/…
阅读更多...
2024最新版鸿蒙纯血原生应用开发教程文档丨HarmonyOS 开发准备-成为华为开发者

2024最新版鸿蒙纯血原生应用开发教程文档丨HarmonyOS 开发准备-成为华为开发者

1. 成为华为开发者 在开始应用开发前&#xff0c;需要先完成以下准备工作。在华为开发者联盟网站上&#xff0c;注册成为开发者&#xff0c;并完成实名认证&#xff0c;从而享受联盟开放的各类能力和服务。 1.1. 注册账号 如果您已经有华为开发者联盟帐号&#xff0c;点击右…
阅读更多...
记录如何在RK3588板子上跑通paddle的OCR模型

记录如何在RK3588板子上跑通paddle的OCR模型

官网文档地址 rknn_zoo RKNPU2_SDK RKNN Model Zoo 一、PC电脑是Ubuntu22.04系统中完成环境搭建(板子是20.04&#xff09; 安装模型转换环境 ​conda create -n rknn2 python3.10 conda activate rknn2 安装Ubuntu依赖包 su…
阅读更多...
CloudStack云平台搭建：XenServer服务器系统安装

CloudStack云平台搭建：XenServer服务器系统安装

1.打开VMware虚拟机&#xff0c;点击“创建新的虚拟机” 2. 点击“自定义&#xff08;高级&#xff09;” → “下一步” 3. 点击“下一步” 4. 点击“稍后安装操作系统” → “下一步” 5. 选择“其他” → “其他64位” → “下一步” 6. 修改“虚拟机名称” 、“位置”&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023