-
计算极限 lim n → ∞ 2024 n ( 1 − cos 1 n 2 ) n 3 1 + n 2 − n \mathop {\lim }\limits_{n \to \infty } \frac{ {\sqrt[n]{ {2024}}\left( {1 - \cos \frac{1}{ { {n^2}}}} \right){n^3}}}{ {\sqrt {1 + {n^2}} - n}} n→∞lim1+n2−nn2024(1−cosn21)n3
lim n → ∞ 2024 n ( 1 − cos 1 n 2 ) n 3 1 + n 2 − n = lim n → ∞ 1 2 ( 1 n 2 ) 2 n 3 ( 1 + n 2 + n ) 1 lim n → ∞ 2024 n = 1 \begin{align*} \lim_{n \to \infty} \frac{\sqrt [n]{2024} \left( 1 - \cos \frac{1}{n^2} \right) n^3}{\sqrt{1 + n^2} - n} &= \lim_{n \to \infty} \frac{\frac{1}{2} \left( \frac{1}{n^2} \right)^2 n^3 \left( \sqrt{1 + n^2} + n \right)}{1} \lim_{n \to \infty} \sqrt [n]{2024} \\ &= 1 \end{align*} n→∞lim1+n2−nn2024(1−cosn21)n3=n→∞lim121(n21)2n3(1+n2+n)n→∞limn2024=1
-
计算定积分 ∫ 0 π cos 2 x e x d x \int_0^\pi \cos^2 x e^x \, \mathrm{d}x ∫0πcos2xexdx
∫ 0 π cos 2 x e x d x + ∫ 0 π sin 2 x e x d x = ∫ 0 π e x d x = e π − 1 ∫ 0 π cos 2 x e x d x − ∫ 0 π sin 2 x e x d x = ∫ 0 π cos 2 x e x d x = ( k 1 cos 2 x + k 2 sin 2 x ) e x ∣ 0 π \begin{align*} \int_0^\pi \cos^2 x e^x \, \mathrm{d}x + \int_0^\pi \sin^2 x e^x \, \mathrm{d}x &= \int_0^\pi e^x \, \mathrm{d}x \\ &= e^\pi - 1 \\ \int_0^\pi \cos^2 x e^x \, \mathrm{d}x - \int_0^\pi \sin^2 x e^x \, \mathrm{d}x &= \int_0^\pi \cos 2x e^x \, \mathrm{d}x \\ &= \left( k_1 \cos 2x + k_2 \sin 2x \right) e^x \bigg|_0^\pi \end{align*} ∫0πcos2xexdx+∫0πsin2xexdx∫0πcos2xexdx−∫0πsin2xexdx=∫0πexdx=eπ−1=∫0πcos2xexdx=(k1cos2x+k2sin2x)ex 0π
由方程组 k 1 + 2 k 2 = 1 {k_1} + 2{k_2} = 1 k1+2k2=1, k 2 − 2 k 1 = 0 {k_2} - 2{k_1} = 0 k2−2k1=0 可得 k 1 = 1 5 {k_1} = \frac{1}{5} k1=51, k 2 = 2 5 {k_2} = \frac{2}{5} k2=52。
( 1 5 cos 2 x + 2 5 sin 2 x ) e x ∣ 0 π = 1 5 ( e π − 1 ) \begin{align*} \left( \frac{1}{5} \cos 2x + \frac{2}{5} \sin 2x \right) e^x \bigg|_0^\pi &= \frac{1}{5} \left( e^\pi - 1 \right) \end{align*} (51cos2x+52sin2x)ex 0π=51(eπ−1)
故原式为 3 5 ( e π − 1 ) \frac{3}{5} \left( e^\pi - 1 \right) 53(eπ−1)。
-
计算曲线积分
∮ C y 1 + x 2 d x + ( 4 x + ln ( x + 1 + x 2 ) ) d y \oint_C \frac{y}{\sqrt{1 + x^2}} \, \mathrm{d}x + \left( 4x + \ln \left( x + \sqrt{1 + x^2} \right) \right) \, \mathrm{d}y ∮C1+x2ydx+(4x+ln(x+1+x2))dy其中曲线 C C C 为从 A ( 1 , 0 ) A(1,0) A(1,0) 到 B ( − 1 , 0 ) B(-1,0) B(−1,0) 的上半圆周,方向为逆时针。
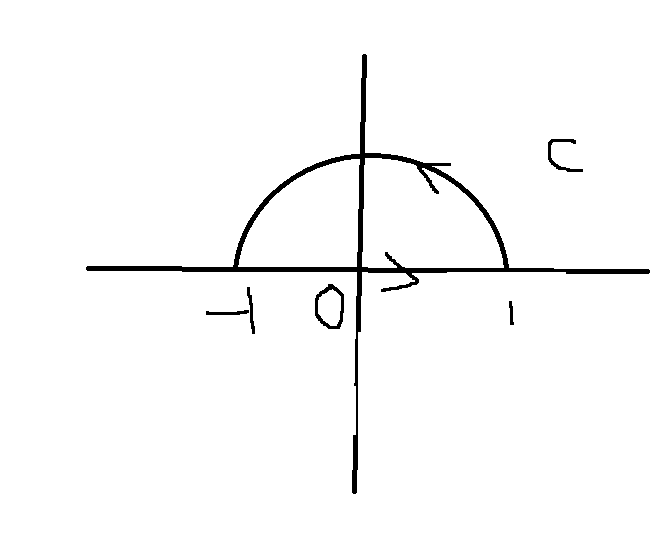
∮ C y 1 + x 2 d x + ln ( x + 1 + x 2 ) d y = ∮ C 4 x d y = ∫ 0 π 4 cos 2 θ d θ = ∫ 0 π 2 ( cos 2 θ + 1 ) d θ = 2 π \begin{align*} \oint_C \frac{y}{\sqrt{1 + x^2}} \, \mathrm{d}x + \ln \left( x + \sqrt{1 + x^2} \right) \, \mathrm{d}y &= \oint_C 4x \, \mathrm{d}y \\ &= \int_0^\pi 4 \cos^2 \theta \, \mathrm{d}\theta \\ &= \int_0^\pi 2 \left( \cos 2\theta + 1 \right) \, \mathrm{d}\theta \\ &= 2\pi \end{align*} ∮C1+x2ydx+ln(x+1+x2)dy=∮C4xdy=∫0π4cos
2024数学分析【南昌大学】
news2026/2/16 14:15:20
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/2224521.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
桥接模式,外界与主机通,与虚拟机不通
一 二 在此选择Windows与外界连接的网卡,通过有线连就选有线网卡,通过无线连就选无线网卡。
三 如果需要设置固定IP,则选择"Manual"进行设置。我这边根据实际需要,走无线的时候用DHCP,走有线的时候设固定IP…
C#生成SVG文件(文本、线段、圆、椭圆、多边形的示例)
1. 介绍 一些参考博客: C#生成SVG涉及文字、线段、椭圆的示例 用C#解析渲染显示SVG矢量图转化格式保存 C#操作SVG矢量图-nuget库svg 开源库:https://github.com/svg-net/SVG 在NuGet上搜索SVG并安装:
2. 示例
引入的命名空间: …
初识算法 · 前缀和(1)
目录
前言:
一维数组的前缀和
题目解析
算法原理
算法编写
二维数组的前缀和
题目解析
算法原理
算法编写 前言:
本文的主题是前缀和,通过两道题目讲解,一道是一维数组的模板,一道是二维数组的模板。 链接…
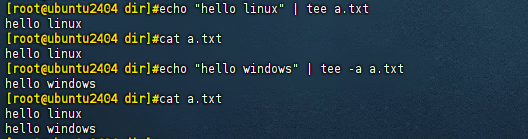
03 文件管理和IO重定向
1 文件系统目录结构 1.1 文件系统目录结构 文件系统的目录结构成树形结构一切文件的路径起点都是从根目录开始,用 / 表示文件名大小写敏感以 . 开头的文件都是隐藏文件路径通过 / 进行分割不同颜色的文件,它的类型是不同的每个文件都有两类数据ÿ…
S-Function
目录 S-Function介绍
生成S-Function的三种常用手段
使用手写S-函数合并定制代码
使用S-Function Builder块合并定制代码
使用代码继承工具合并定制代码 S-Function介绍
我们可以使用S-Function扩展Simulink对仿真和代码生成的支持。例如,可以使用它们…
初识Linux · 动静态库(incomplete)
目录
前言:
静态库
动态库 前言:
继上文,我们从磁盘的理解,到了文件系统框架的基本搭建,再到软硬链接部分,我们开始逐渐理解了为什么运行程序需要./a.out了,这个前面的.是什么我们也知道了。…
探索 Python 幽默之源:pyjokes 库全解析
🚀 探索 Python 幽默之源:pyjokes 库全解析
1. 背景介绍:为何选择 pyjokes?
在紧张的编程工作中,幽默是一种有效的缓解压力的方式。pyjokes 是一个专为程序员设计的 Python 库,它提供了丰富的单行笑话&am…
vscode配色主题与图标库推荐
vscode配色主题推荐:Andromedavsocde图标库: vscode-icons
Andromeda Dark theme with a taste of the universe 仙女座:一套宇宙深空体验的哑暗色主题; 高对比度,色彩饱和; Easy Installation
Open the extensions sidebar on Visual Studio CodeSear…
定时任务使用kafka
定时任务使用kafka
在上述业务场景中使用 Kafka 而不是直接定时执行任务有以下几个重要原因: 一、解耦 任务触发与执行分离: 使用 XXL-JOB 定时触发任务并将任务消息发送到 Kafka,实现了任务触发端(通常是调度系统)和…
C++,STL 049(24.10.26)
内容
pair的基本概念及构建方式。 运行代码
#include <iostream>
#include <string>using namespace std;void test01()
{// pair将2个数据组合成一组数据来使用(first 、second)// 注意pair的使用可以不添加头文件pair<string, int>…
Golang | Leetcode Golang题解之第501题二叉搜索树中的众数
题目: 题解:
func findMode(root *TreeNode) (answer []int) {var base, count, maxCount intupdate : func(x int) {if x base {count} else {base, count x, 1}if count maxCount {answer append(answer, base)} else if count > maxCount {ma…
实验干货|电流型霍尔传感器采样设计02-有源滤波设计
在上一篇博客中,介绍了如何通过跨阻放大器,将霍尔输出的电流转换成电压。本篇博客继续介绍,如何将得到的电压进行滤波。
有源滤波和无源滤波的选择
简单来说,对于采样电路而言,无源滤波一般选择RC滤波,RC…
【K8S系列】Kubernetes Service 基础知识 详细介绍
在 Kubernetes 中,Service 是一种抽象的资源,用于定义一组 Pod 的访问策略。它为这些 Pod 提供了一个稳定的访问入口,解决了 Pod 可能频繁变化的问题。本文将详细介绍 Kubernetes Service 的类型、功能、使用场景、DNS 和负载均衡等方面。 1.…
使用FRP搭建内网穿透服务(新版toml配置文件,搭配反向代理方便内网网站访问)【使用frp搭建内网穿透】
FRP(Fast Reverse Proxy)是一个高性能的反向代理应用程序,主要用于内网穿透。它允许用户将内部网络服务暴露到外部网络,适用于 NAT 或防火墙环境下的服务访问。 他是一个开源的 服务 如果大家不想用 花生壳 软件,可以尝…
遗传算法(Genetic Algorithm)理论详解
遗传算法(Genetic Algorithm,GA)是一种模拟自然界生物进化过程与机制的随机搜索与优化算法,被广泛应用于计算机科学、工程技术、经济学等众多领域。
1. 基本原理
1.1 生物遗传学类比 遗传算法的灵感来源于达尔文的进化论。在自然…
订购 Claude AI 的第二天 它独自完成 文字转语音 flask应用
图二里,删除几个无关的 chats
全程我做的工作:向 AI 提要求,copy / paste 代码,在venv验证运行,向 AI 反馈,总共用了3个 chats.(图中的只有一个 Chat, 删掉的另外两个: Python 库安…
背包问题(位运算优化、bitset)
3180. 执行操作可获得的最大总奖励| . - 力扣(LeetCode)
给你一个整数数组 rewardValues,长度为 n,代表奖励的值。
最初,你的总奖励 x 为 0,所有下标都是 未标记 的。你可以执行以下操作 任意次 …
数字IC后端实现 | Innovus各个阶段常用命令汇总
应各位读者要求,小编最近按照Innovus流程顺序整理出数字IC后端项目中常用的命令汇总。限于篇幅,这次只更新到powerplan阶段。有了这份Innovus常用命令汇总,学习数字IC后端从此不再迷路!如果大家觉得这个专题还不错,想继…
Linux 字符设备驱动 之 无法归类的《杂项设备驱动》
学习目标:
了解 杂项设备驱动 和普通字符设备的异同,及杂项设备驱动程序的写法 学习内容:
一、杂项设备驱动的特别之处 杂项设备(Miscellaneous Devices)是一种通用的设备类型,用于表示那些不适合其他设备…
LeetCode 热题 100之普通数组
1.最大子数组和 思路分析:这个问题可以通过动态规划来解决,我们可以使用Kadane’s Algorithm(卡登算法)来找到具有最大和的连续子数组。 Kadane’s Algorithm 的核心思想是利用一个变量存储当前的累加和 currentSum,并…