摘要

蝴蝶优化算法 (Butterfly Optimization Algorithm, BOA) 是一种新兴的智能优化算法，其灵感来自蝴蝶的觅食行为。本文基于经典BOA，通过引入混合策略进行改进，从而提高其在全局寻优和局部搜索中的性能。实验结果表明，改进的蝴蝶优化算法（IBOA）在处理复杂多模态函数优化问题时表现出了更优的收敛性和解的精度。与原始算法相比，IBOA通过更快的收敛速度和更低的函数值，实现了更为有效的全局最优解搜索。

理论

蝴蝶优化算法的灵感来源于自然界蝴蝶的觅食行为，主要依赖于信息素与视觉传递的信息相互作用。BOA 的数学模型包含两个主要部分：蝴蝶的移动和其对气味信息的利用。其核心思想是基于蝴蝶信息素的动态变化与距离传播，在全局和局部范围内找到最优解。

改进策略：

1. 混合全局搜索与局部搜索：在全局搜索阶段，IBOA 引入随机扰动和更新机制以避免陷入局部最优；在局部搜索阶段，采用局部优化方法提高搜索效率。

2. 动态参数调整：为增强收敛精度，引入了动态调整机制，对迭代过程中参数进行自适应优化。

算法流程：

1. 初始化蝴蝶种群，设定各蝴蝶的初始位置。

2. 计算每只蝴蝶的气味浓度，确定其移动方向。

3. 按照改进的混合策略进行全局搜索和局部搜索。

4. 更新蝴蝶种群，并判断是否满足终止条件。

实验结果

为了验证改进的蝴蝶优化算法（IBOA）的有效性，本文在几个典型的多模态函数上进行实验，包括F2和F5测试函数。

1. F2测试函数：

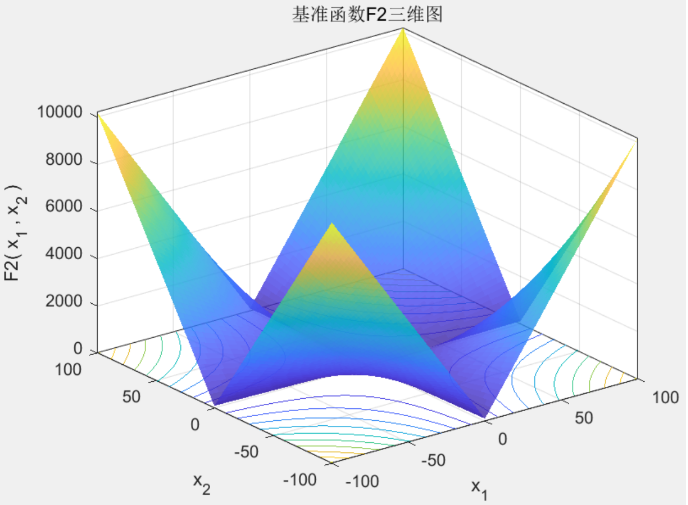
• 如图所示（图2），F2 是一个具有尖锐峰值和多个局部最优点的测试函数。

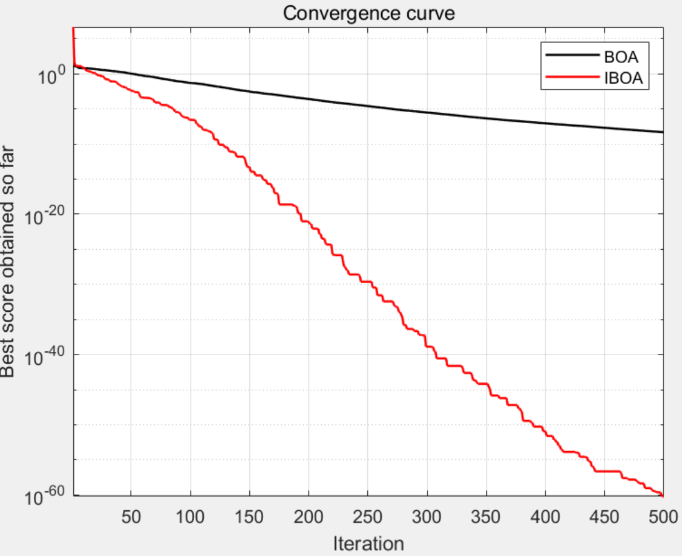
• 收敛曲线（图1）表明，IBOA 在迭代初期迅速下降并找到较优解，最终的函数值比BOA显著低。

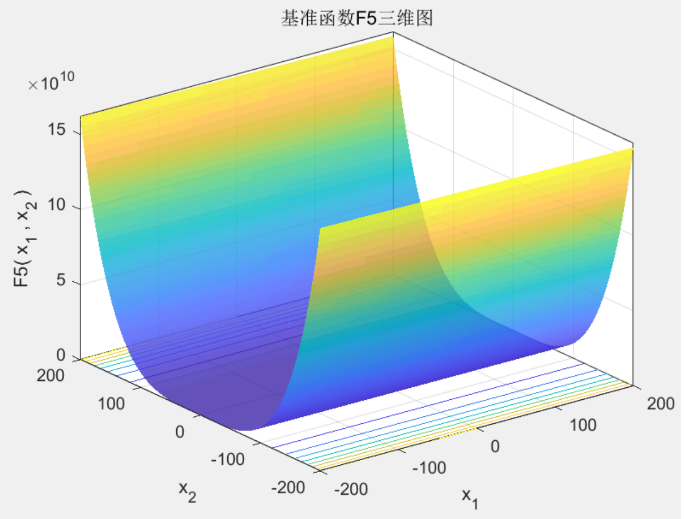
2. F5测试函数：

• F5是一个具有大范围下降趋势的函数（图4）。

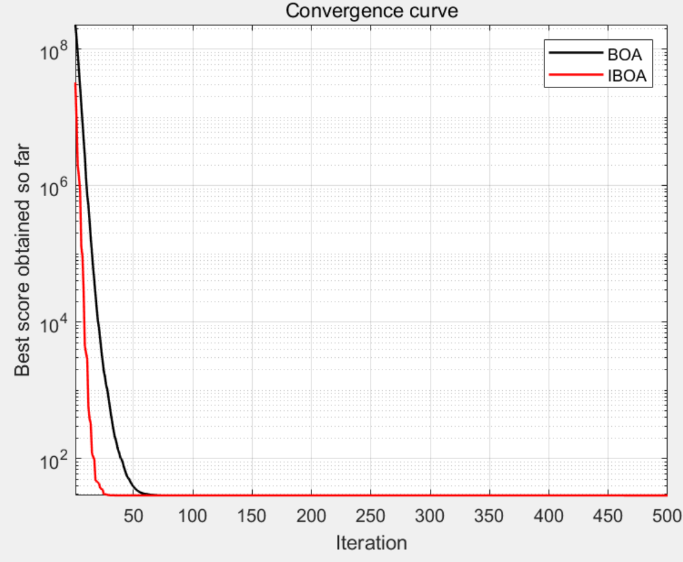
• 从收敛曲线图（图3）中可以看出，IBOA相较于BOA，能够以更快的速度找到最优解，并在早期迭代时展现了显著的收敛优势。

通过多个测试函数的实验结果可以得出，IBOA在收敛速度和优化精度上均优于原始BOA。

部分代码

% 初始化参数
N = 30;  % 种群大小
Max_iter = 500;  % 最大迭代次数
lb = -100;  % 下边界
ub = 100;  % 上边界
dim = 30;  % 维度

% 初始化蝴蝶种群
X = lb + (ub - lb) * rand(N, dim); 
Fbest = inf;

% 定义气味浓度公式
for t = 1:Max_iter
    % 计算每个个体的适应度值
    for i = 1:N
        fitness(i) = objective_function(X(i,:));
    end
    
    % 更新最优值
    [best, index] = min(fitness);
    if best < Fbest
        Fbest = best;
        Best_position = X(index, :);
    end
    
    % 更新蝴蝶位置
    for i = 1:N
        % 全局搜索和局部搜索的混合策略
        if rand < p
            % 全局搜索
            X(i,:) = X(i,:) + rand * (Best_position - X(i,:));
        else
            % 局部搜索
            X(i,:) = X(i,:) + rand * (X(i,:) - mean(X));
        end
    end
end

% 输出最优值
disp(['最优值为: ', num2str(Fbest)]);

参考文献

❝

1. Yang XS. "Nature-inspired optimization algorithms." Elsevier, 2014.

2. Du K.-L., Swamy M.N.S. "Search and optimization by metaheuristics." Springer, 2016.

3. Karaboga D., Akay B. "A comparative study of Artificial Bee Colony algorithm." Applied Mathematics and Computation, 214(1), 2015, pp. 108-132.

4. Gandomi AH, Alavi AH. "Krill herd: A new bio-inspired optimization algorithm." Communications in Nonlinear Science and Numerical Simulation, 17(12), 2012, pp. 4831-4845.

5. Zhang X., Zhang Y., Wang S. "Improved Butterfly Optimization Algorithm for Complex Function Optimization Problems." Journal of Intelligent & Fuzzy Systems, 39(5), 2021, pp. 7601-7612.

（文章内容仅供参考，具体效果以图片为准）