【2024】【字节青训营】：字节青训营入营测试题—

简单题目

计算x到y的最小步数

环状 DNA 序列的最小表示法

Base32 解码和编码

打点计时器

兔群繁殖之谜

完美整数

找出整数数组中占比超过一半的数

找出最长的神奇数列

找单独的数

字符串最短循环字串

二进制反码转换问题

中等题目

简单四则运算

数字翻译成字符串有多少种可能性

最大异或和计算

五子棋获胜策略

困难题目

二进制之和

查找热点数据

要求：

简单题不少于10道题

中等题目不少于4道题

困难题目不少于1道题

介绍：

本次24青训营，入营和之前的考核模型有所不同，之前是做题，几十个选择题，两道算法题，一道简答题，现在则是在ai的辅助下进行刷题考核，这么做的原因无非是推广自己家的智能编码助手，还有就是此次代码考核在在线平台上，就能得到大量的数据，然后使用这些数据去强化编码助手，最后就是ai助手有点傻，一个是你把他给你的代码，都过不了示例，然后他容易顺着你代码的想法，往后推理，如果你一开始的想法不对，就会进入死角。

简单题目

已完成 11 成功提交 10

兔群繁殖之谜样例通过，提交失败

计算x到y的最小步数

# 问题描述

AB 实验同学每天都很苦恼如何可以更好地进行 AB 实验，每一步的流程很重要，我们目标为了缩短所需的步数。

我们假设每一步对应到每一个位置。从一个整数位置 `x` 走到另外一个整数位置 `y`，每一步的长度是正整数，每步的值等于上一步的值 `-1`， `+0`，`+1`。求 `x` 到 `y` 最少走几步。并且第一步必须是 `1`，最后一步必须是 `1`，从 `x` 到 `y` 最少需要多少步。

## 样例说明

- 整数位置 `x` 为 `12`，另外一个整数位置 `y` 为 `6`，我们需要从 `x` 走到 `y`，最小的步数为：`1`，`2`，`2`，`1`，所以我们需要走 `4` 步。
- 整数位置 `x` 为 `34`，另外一个整数位置 `y` 为 `45`，我们需要从 `x` 走到 `y`，最小的步数为：`1`，`2`，`3`，`2`，`2`，`1`，所以我们需要走 `6` 步。
- 整数位置 `x` 为 `50`，另外一个整数位置 `y` 为 `30`，我们需要从 `x` 走到 `y`，最小的步数为：`1`，`2`，`3`，`4`，`4`，`3`，`2`，`1`，所以我们需要走 `8` 步。

## 输入格式

输入包含 `2` 个整数 `x`，`y`。（`0<=x<=y<2^31`）

## 输出格式

对于每一组数据，输出一行，仅包含一个整数，从 `x` 到 `y` 所需最小步数。

## 输入样例

```
12 6
34 45
50 30
```

## 输出样例

```
4
6
8
```

问题分析：

从x走到y，其实就是从步伐大小从1开始走，最后一步也必须为1，每一步之间呢，可以+1，0，和-1，如果说想要最小步数，这个步伐肯定要迈的大，我的代码呢，遵循一个原则，就是第一步肯定为1，接下来每一步有三种选择，假设步伐为x，一个是x + 1，一个是x，一个是x - 1，在优先级上x + 1 > x > x - 1,在是否合规上采取走下一步的时候，必须保证剩余的距离，可以降到 1 ，也就是说先 x + 1，但是剩下的距离必须大于等于 x~1的和，如果不可以那就尝试 x，剩下的距离大于等于 x - 1 ~ 1 的he，x - 1也是如此，直至走到y。

代码如下：

public class Main {
    public static int sum(int x) {
        if (x <= 0) {
            return 0;
        }
        int res = 0;
        for (int i = 1; i <= x; i++) {
            res += i;
        }
        return res;
    }

    // Calculate the minimum steps from x to y
    public static int solution(int x, int y) {
        if (x > y) {
            int temp = x;
            x = y;
            y = temp;
        }
        int l = 0, r = y - x;
        int step = 0;
        int stepDistance = 0;

        while (l < r) {
            if (step == 0) {
                stepDistance = 1;
                step = 1;
                l += stepDistance;
                continue;
            }

            int step1 = stepDistance + 1;
            int step2 = stepDistance;
            int step3 = stepDistance - 1;

            if (l + step1 < r) {
                int m = l + step1;
                int s = sum(step1 - 1);
                if ((r - m) >= s) {
                    l = m;
                    step++;
                    stepDistance = step1;
                    continue;
                }
            }
            if (l + step2 <= r) {
                int m = l + step2;
                int s = sum(step2 - 1);
                if ((r - m) >= s) {
                    l = m;
                    step++;
                    stepDistance = step2;
                    continue;
                }
            }
            if (l + step3 <= r) {
                int m = l + step3;
                int s = sum(step3 - 1);
                if ((r - m) >= s) {
                    l = m;
                    step++;
                    stepDistance = step3;
                    continue;
                }
            }
        }

        return step;
    }

    public static void main(String[] args) {
        // Add your test cases here
        System.out.println(solution(6, 7) == 1);      // Should print true
        System.out.println(solution(12, 6) == 4);     // Should print true
        System.out.println(solution(34, 45) == 6);    // Should print true
        System.out.println(solution(50, 30) == 8);     // Should print true
    }
}

运行结果：

环状 DNA 序列的最小表示法

# 问题描述

环状 DNA 又称超螺旋，即一段碱基序列呈现环状，在分析时，需要将相同序列的环状 DNA 分到相同组内，现需将环状碱基序列按照最小表示法进行排序。

一段长度为 `n` 的碱基序列，按照顺时针方向，碱基序列可以从任意位置起开始该序列顺序，因此长度为 `n` 的碱基序列有 `n` 种表示法。例如：长度为 6 的碱基序列 `CGAGTC`，有 `CGAGTC`、`GAGTCC`、`AGTCCG` 等表示法。在这些表示法中，字典序最小的称为“最小表示”。

输入一个长度为 `n`（`n <= 100`）的环状碱基序列（只包含 `A`、`C`、`G`、`T` 这 4 种碱基）的一种表示法，输出该环状碱基序列的最小表示。

例如：
`ATCA` 的最小表示是 `AATC`
`CGAGTC` 的最小表示是 `AGTCCG`

## 输入描述

一段 DNA 碱基序列

## 输出描述

DNA 碱基序列的最小表示

**备注**：
`n <= 100`
DNA 由大写英文字母 `A`、`G`、`C`、`T` 组成

**示例 1**
输入：`ATCA`
输出：`AATC`

**示例 2**
输入：`CGAGTC`
输出：`AGTCCG`

问题分析：

通过循环将所有的可能存储起来，然后循环比较得出最小的DNA碱基序列

代码如下：

import java.util.ArrayList;
import java.util.List;

public class Main {
    public static String solution(String dna_sequence) {
        // Create a list to hold the different representations of the DNA sequence
        List<String> representations = new ArrayList<>();
        int length = dna_sequence.length();

        // Generate all rotations of the DNA sequence
        for (int i = 0; i < length; i++) {
            String representation = dna_sequence.substring(i) + dna_sequence.substring(0, i);
            representations.add(representation);
        }

        // Find the minimum representation
        String minRepresentation = representations.get(0);
        for (String representation : representations) {
            if (representation.compareTo(minRepresentation) < 0) {
                minRepresentation = representation;
            }
        }

        return minRepresentation;
    }

    public static void main(String[] args) {
        // Add your test cases here
        System.out.println(solution("ATCA").equals("AATC")); // Should print true
        System.out.println(solution("CGAGTC").equals("AGTCCG")); // Should print true
        System.out.println(solution("TCATGGAGTGCTCCTGGAGGCTGAGTCCATCTCCAGTAG")
                .equals("AGGCTGAGTCCATCTCCAGTAGTCATGGAGTGCTCCTGG")); // Should print true
    }
}

运行结果：

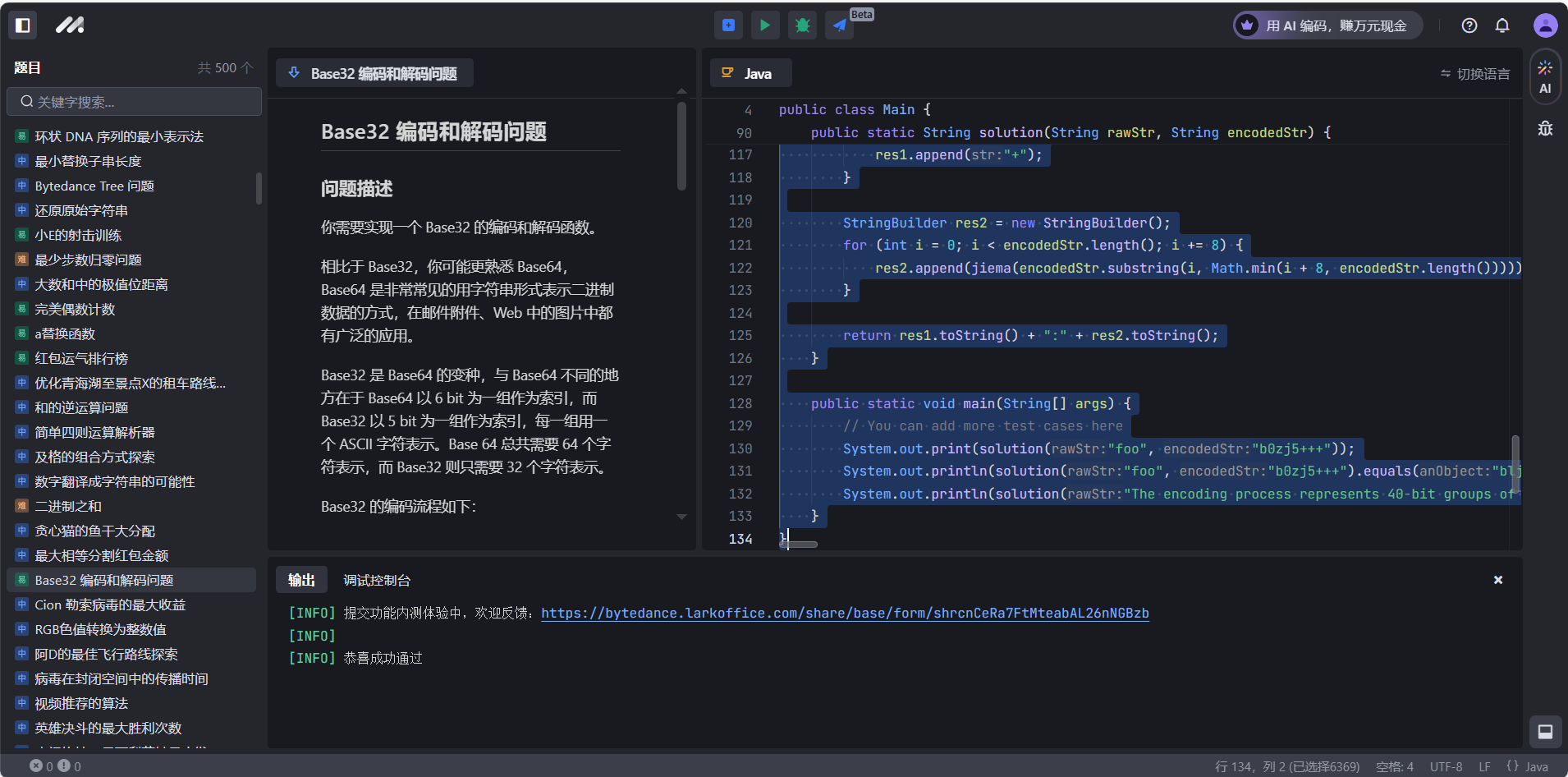
Base32 解码和编码

# 问题描述

你需要实现一个 Base32 的编码和解码函数。

相比于 Base32，你可能更熟悉 Base64，Base64 是非常常见的用字符串形式表示二进制数据的方式，在邮件附件、Web 中的图片中都有广泛的应用。

Base32 是 Base64 的变种，与 Base64 不同的地方在于 Base64 以 6 bit 为一组作为索引，而 Base32 以 5 bit 为一组作为索引，每一组用一个 ASCII 字符表示。Base 64 总共需要 64 个字符表示，而 Base32 则只需要 32 个字符表示。

Base32 的编码流程如下：
- 对二进制数据进行预处理：如果二进制数据的 bit 数目不不是 5 的倍数的话，在末尾补 0 直至为 5 的倍数
- 以 5 bit 为一组进行分组
- 将每一组的 5 bit 二进制转换为索引（0 - 31）
- 在索引 - 字符转换表中查询索引对应的字符
- 根据原始二进制数据的 bit 数目除以 40 后的余数，确定末尾需要补 0 的数目
  - 如果原始二进制数据 bit 数目除以 40 后的余数是 0 的话，不需要补 +
  - 如果原始二进制数据 bit 数目除以 40 后的余数是 8 的话，补 6 个 +
  - 如果原始二进制数据 bit 数目除以 40 后的余数是 16 的话，补 4 个 +
  - 如果原始二进制数据 bit 数目除以 40 后的余数是 24 的话，补 3 个 +
  - 如果原始二进制数据 bit 数目除以 40 后的余数是 32 的话，补 1 个 +

Base32 的索引 - 字符转换表见下方。

索引：0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

字符：9 8 7 6 5 4 3 2 1 0 m  n  b  v  c  x  z  a  s  d  f  g  h  j  k  l  p  o  i  u  y  t

**示例**

**编码**

- 输入：字符串 `foo`
- 字符 `f` 的 ASCII 编号为 102，字符 `o` 的 ASCII 编号为 111
- 将字符串 `foo` 以 ASCII 编号形式表达为 102 111 111 的序列
- 将 102 111 111 的序列转换为二进制表示，即 01100110 01101111 01101111，将二进制字符串以 40 个为一组进行分割
- 最后一组的二进制字符串长度为 24，不是 5 的倍数，因此在最后补 0，直至其能被 5 整除（在此例子中，补 1 个即可），二进制字符串表示为： 01100110 01101111 01101111 0
- 每 5 bit 为一组，表示为：01100 11001 10111 10110 11110
- 将每一组转换为十进制的索引，表示为：12 25 23 22 30，对应字符 `b` `l` `j` `h` `y`
- 由于最终输出字符串长度不是 8 的倍数，在输出最后补充 3 个 `+`
- 查询索引 - 字符转换表后，可以得出最终的输出为：`bljhy+++`

`Input data: foo`
`Input in Unicode: 102 111 111`
`Unicode in binary (8-bit): 01100110 01101111 01101111 0`
`Unicode in binary (5-bit): 01100 11001 10111 10110 11110`
`Decimal: 12 25 23 22 30`
`Pad: + + +`
`Output: b l j h y + + +`

**解码**

- 输入：`bljhy+++`
- 查询索引 - 字符转换表后，可知原始的二进制数据组为：01100 11001 10111 10110 11110
- 由末尾 3 个 `+` 可知在编码时原始二进制数据最后一组的个数为 24 个，由此可知最后一组数据为：01100110 01101111 01101111
- 将二进制数据转换为 ASCII 编号后可知，原始字符串的 Unicode 序列为：102 111 111
- 将 Unicode 序列转换为字符串，即可得出原始字符串，为：`foo`

**输入示例**

`foo`
`b0zj5+++`

- 第一行为需要编码的原始字符串：`rawStr`
- 第二行为需要解码的 Base32 字符串：`encodedStr`

**输出示例**

`bljhy+++`
`bar`

**解释**：
- 第一行编码后的输出为 `bljhy+++`
- 第二行解码后的输出为 `bar`

**数据范围**

`rawStr[n]` 为 ASCII 的可显示字符，`rawStr.length < 2048`
`encodedStr` 为使用此算法编码后的 Base32 字符序列，`encodedStr.length < 4096`

问题分析：

这个题目不是很难，但是很繁琐，可能是我的实现问题的原因，我写了很多函数，

各个函数的作用：

`decimalToBinary8Bits` 用于将十进制数转换为 8 位二进制字符串，

`binaryToDecimal` 用于将二进制字符串按 5 位一组转换为十进制数并存入向量，

`decimalArrayToBinary` 用于将十进制数向量转换为二进制字符串，

`binaryToChar` 用于将二进制字符串按 8 位一组转换为 ASCII 码对应的字符。

`jiema` 函数用于解码操作，通过判断输入字符串末尾的 `+` 个数来确定原始二进制数据的长度，然后进行解码处理。但这个函数中的条件判断较多，可能会增加理解和维护的难度。

`solution` 函数是主要的处理函数，它对输入的原始字符串进行预处理，转换为二进制字符串并根据余数进行补零，然后进行编码和解码操作。

代码如下：

import java.util.ArrayList;
import java.util.List;

public class Main {
    static char[] base32 = {
        '9', '8', '7', '6', '5', '4', '3', '2', '1', '0', 
        'm', 'n', 'b', 'v', 'c', 'x', 'z', 'a', 's', 'd', 
        'f', 'g', 'h', 'j', 'k', 'l', 'p', 'o', 'i', 'u', 
        'y', 't'
    };

    public static String decimalToBinary8Bits(int num) {
        StringBuilder binary = new StringBuilder();
        for (int i = 7; i >= 0; i--) {
            binary.append((num & (1 << i)) != 0 ? '1' : '0');
        }
        return binary.toString();
    }

    public static List<Integer> binaryToDecimal(String binaryStr) {
        List<Integer> decimalNums = new ArrayList<>();
        for (int i = 0; i < binaryStr.length(); i += 5) {
            String group = binaryStr.substring(i, Math.min(i + 5, binaryStr.length()));
            int decimal = 0;
            for (char c : group.toCharArray()) {
                decimal = decimal * 2 + (c - '0');
            }
            decimalNums.add(decimal);
        }
        return decimalNums;
    }

    public static String decimalArrayToBinary(List<Integer> arr) {
        StringBuilder result = new StringBuilder();
        for (int num : arr) {
            StringBuilder binary = new StringBuilder();
            for (int i = 4; i >= 0; i--) {
                binary.append((num & (1 << i)) != 0 ? '1' : '0');
            }
            result.append(binary);
        }
        return result.toString();
    }

    public static String binaryToChar(String binaryStr) {
        StringBuilder result = new StringBuilder();
        for (int i = 0; i < binaryStr.length(); i += 8) {
            String group = binaryStr.substring(i, Math.min(i + 8, binaryStr.length()));
            int decimal = 0;
            for (char c : group.toCharArray()) {
                decimal = decimal * 2 + (c - '0');
            }
            result.append((char) decimal);
        }
        return result.toString();
    }

    public static String jiema(String encodedStr) {
        int i;
        for (i = encodedStr.length() - 1; i > 0 && encodedStr.charAt(i) == '+'; i--);
        String newstr = encodedStr.substring(0, i + 1);
        List<Integer> st2 = new ArrayList<>();
        for (char c : newstr.toCharArray()) {
            for (int j = 0; j < base32.length; j++) {
                if (c == base32[j]) {
                    st2.add(j);
                }
            }
        }
        String newnewstr = decimalArrayToBinary(st2);
        String res2 = "";

        if (newnewstr.length() % 40 == 10) {
            String newstrs = newnewstr.substring(0, newnewstr.length() - 2);
            res2 = binaryToChar(newstrs);
        } else if (newnewstr.length() % 40 == 20) {
            String newstrs = newnewstr.substring(0, newnewstr.length() - 4);
            res2 = binaryToChar(newstrs);
        } else if (newnewstr.length() % 40 == 25) {
            String newstrs = newnewstr.substring(0, newnewstr.length() - 1);
            res2 = binaryToChar(newstrs);
        } else if (newnewstr.length() % 40 == 35) {
            String newstrs = newnewstr.substring(0, newnewstr.length() - 3);
            res2 = binaryToChar(newstrs);
        }

        return res2;
    }

    public static String solution(String rawStr, String encodedStr) {
        List<Integer> st = new ArrayList<>();
        StringBuilder str1 = new StringBuilder();

        for (char c : rawStr.toCharArray()) {
            str1.append(decimalToBinary8Bits(c));
        }

        int r = str1.length() % 40;
        if (r == 8) {
            str1.append("00");
        } else if (r == 16) {
            str1.append("0000");
        } else if (r == 24) {
            str1.append("0");
        } else if (r == 32) {
            str1.append("000");
        }

        st = binaryToDecimal(str1.toString());
        StringBuilder res1 = new StringBuilder();

        for (int value : st) {
            res1.append(base32[value]);
        }

        while (res1.length() % 8 != 0) {
            res1.append("+");
        }

        StringBuilder res2 = new StringBuilder();
        for (int i = 0; i < encodedStr.length(); i += 8) {
            res2.append(jiema(encodedStr.substring(i, Math.min(i + 8, encodedStr.length()))));
        }

        return res1.toString() + ":" + res2.toString();
    }

    public static void main(String[] args) {
        // You can add more test cases here
        System.out.print(solution("foo", "b0zj5+++"));
        System.out.println(solution("foo", "b0zj5+++").equals("bljhy+++:bar")); // Should print true
        System.out.println(solution("The encoding process represents 40-bit groups of input bits as output strings of 8 encoded characters.  Proceeding from left to right, a 40-bit input group is formed by concatenating 5 8bit input groups. These 40 bits are then treated as 8 concatenated 5-bit groups, each of which is translated into a single character in the base 32 alphabet.  When a bit stream is encoded via the base 32 encoding, the bit stream must be presumed to be ordered with the most-significant-bit first. That is, the first bit in the stream will be the high-order bit in the first 8bit byte, the eighth bit will be the low-order bit in the first 8bit byte, and so on.", "bljhy+++b0zj5+++").equals("maf3m164vlahyl60vlds9i6svuahmiod58l3mi6sbglhmodfcbz61b8vb0fj1162c0jjmi6d58jhb160vlk2mu89b0fj1il9b4ls9oogcak2mu89cvp25pncbuls9oo359i79lncbvjh1ln558ahzknsb4aj1lnscbj7917zc0jh3ln4bafhill9bll3yo09vashbu89cajs9id0buf21n89b5z61b8vb0fj1160vlk2mu89bul3yunz58fj3163vul3pln558a2s166vuj33knfbgj37u60vlds9v0928a3su89v4j29unf58dj5oogc8lsi17fv8sj3l093zk79kd0cals9knsbfz21p64vkz21id4b4p3ml89b4ls9c89bvjhiko8cashiknfbgs79v0vb0fj1162c0jjmi6d4zz3mkn6v9z3yla9cuf3sko158fj316fc0zhiiobb4p3ml89v4j21ol9b5z23pncbuh3m166v8zj5kn6casj5160vkz21p6458a37io459ld5168vak3zkn7bgp7i189muf3moa9b5z35pnf58lj1id4b4hs9pnd58shikoxbash116hv4zs9u61bfz35kndbfz63ba9bgj33oo5v4j3cn89caf3m167v4p79iofc0sh7o09vgpj3u89b0ss9i6sbgljmon4bzz21ol9b0ss9oosbasj5ln558ohsu6158p3zl09vgjj3u8vcvfhcod0blfh3kncczhs9kd0czz3bpnscvp7i17fv8zj1160cbh79u61bfz3bpnscvp79kd0czz3soa9caf3m16dcal3mknv58ohso6b58a3m16fv8ss9p60buf7p16xc0s3mia9b0fj1160vkz21p6458d3siddczz6zkd0czz35ynfbfh79u61bfz3mpn2v8p3z167v4p79uo0vah79kd458p3zl09vajjcn09vul31lns58a3su89v4j79u61bfz3bpnscvp79c67v4p79kdlcassk168vls79iox58jhinz+:foobar")); // Should print true
    }
}

运行结果：

打点计时器

# 问题描述

小明想发明一台打点计数器，这个计数器有这样的一个功能：

- 它可以接收一个递增的数据范围（形如[3, 9]），其中第一个数字代表起始，第二个数字代表结束

- 这个数据范围中包含几个数字，打点计数器就会打几个点

- 在传入的多组数据范围中，如果出现了范围的重复，机器则不会重复打点

你可以帮助小明算一算，在不同的情况下，计数器会打出几个点么？

## 输入格式

一个二维数组

## 输出格式

一个整数，表达在输入是这个数组的情况下，计数器打出的点数

**输入样例(1)**

[
   [1,4],
   [7, 10],
   [3, 5]
]

**输出样例(1)**

7

**输入样例(2)**

[
   [1,2],
   [6, 10],
   [11, 15]
]

**输出样例(2)**

9

**数据范围**

- 数字范围 [-10^9, 10^9]，数组长度 < 2^16

问题分析：

本题目采用集合来处理，因为集合具有互异性，所以在打点过程中重复区域的会被去掉，遍历每段区间，区间遍历每个点，存进集合中，最后返回集合的大小就是打点的数量

代码如下：

import java.util.HashSet;
import java.util.Set;

public class Main {
    public static int solution(int[][] inputArray) {
        // Create a set to store unique integers
        Set<Integer> mySet = new HashSet<>();

        // Iterate through the input ranges
        for (int[] range : inputArray) {
            int start = range[0];
            int end = range[1];
            for (int i = start; i < end; i++) {
                mySet.add(i); // Add each integer in the range to the set
            }
        }

        return mySet.size(); // Return the size of the set which represents the unique integers
    }

    public static void main(String[] args) {
        // Add your test cases here
        int[][] testArray1 = {{1, 4}, {7, 10}, {3, 5}};
        int[][] testArray2 = {{1, 2}, {6, 10}, {11, 15}};

        System.out.println(solution(testArray1) == 7); // Should print true
        System.out.println(solution(testArray2) == 9); // Should print true
    }
}

运行结果：

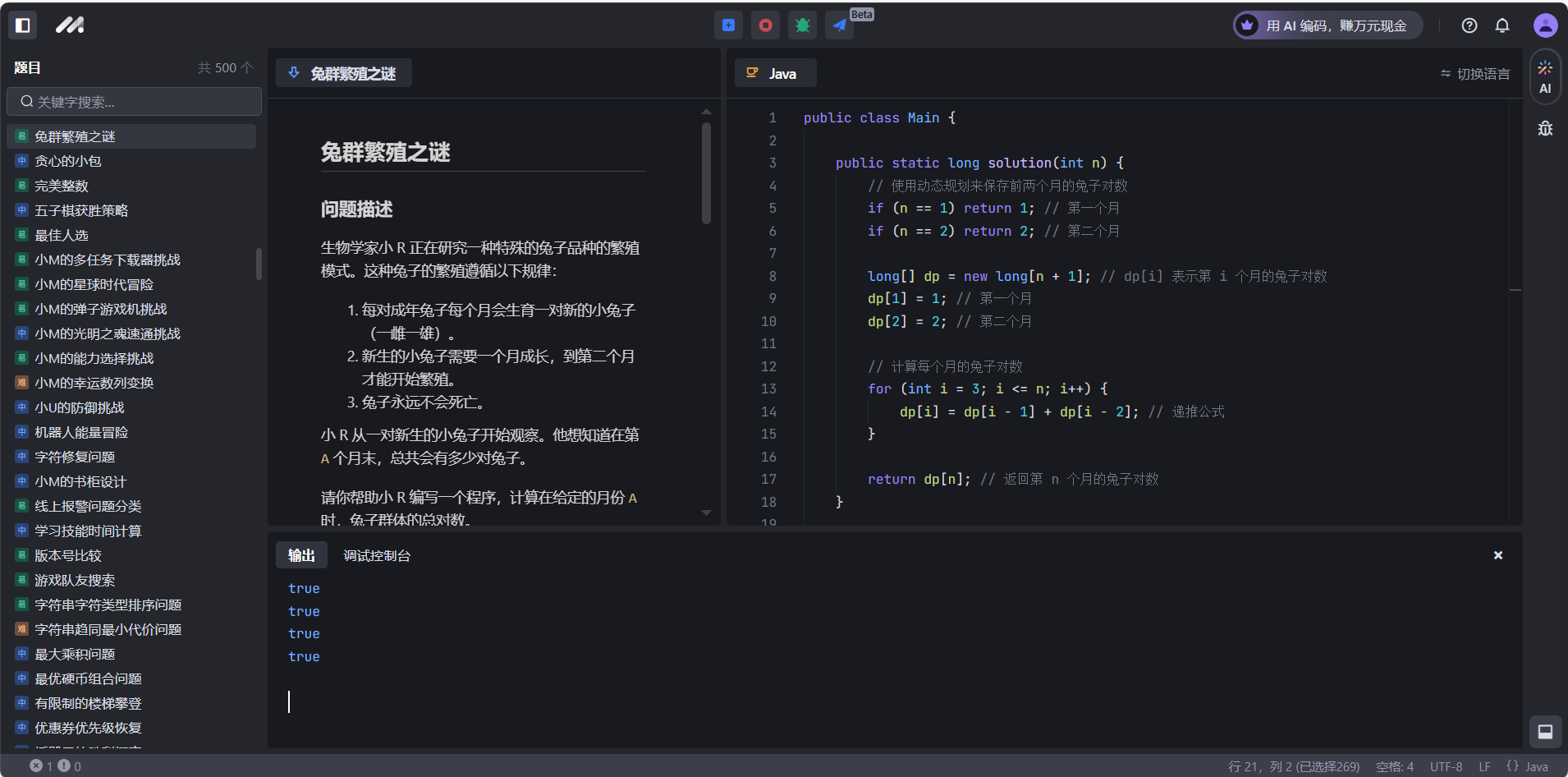
兔群繁殖之谜

# 问题描述
- 如果一对兔子每月生一对兔子；一对新生兔，从第二个月起就开始生兔子；假定每对兔子都是一雌一雄，试问一对兔子，第 `n` 个月能繁殖成多少对兔子？（举例，第1个月是1对兔子，第2个月是2对兔子）

## 输入格式
- 数字

## 输出格式
- 数字

## 输入样例
- 5

## 输出样例
- 8

## 数据范围
- `[1, 75]`

## 测试数据集
  - 样例1
    - 输入：`5`
    - 输出：`8`
  - 样例2
    - 输入：`1`
    - 输出：`1`
  - 样例3
    - 输入：`15`
    - 输出：`987`
  - 样例4
    - 输入：`50`
    - 输出：`20365011074`

问题分析：

函数定义：

- int solution(int n)：这个函数接受一个整数 n 作为输入，并返回第 n 个月兔子的对数。

基本情况处理：

- 如果 n 是 1 或 2，函数直接返回 1 或 2，这是斐波那契数列的前两个数（或在这个问题中，第一个月和第二个月的兔子对数）。

动态规划数组：

- vector<int> dp(n + 1)：创建了一个大小为 n + 1 的动态规划数组 dp，用于存储从第 1 个月到第 n 个月的兔子对数。
- dp[1] = 1 和 dp[2] = 2：初始化前两个月的兔子对数。

递推公式：

- for (int i = 3; i <= n; i++)：从第 3 个月开始，使用递推公式 dp[i] = dp[i - 1] + dp[i - 2] 计算每个月的兔子对数。这个公式基于斐波那契数列的定义，即每个数都是前两个数的和。

返回结果：

- return dp[n]：返回第 n 个月的兔子对数

代码如下：

public class Main {  
      
    public static long solution(int n) {  
        // 使用动态规划来保存前两个月的兔子对数  
        if (n == 1) return 1; // 第一个月  
        if (n == 2) return 2; // 第二个月  
  
        long[] dp = new long[n + 1]; // dp[i] 表示第 i 个月的兔子对数  
        dp[1] = 1; // 第一个月  
        dp[2] = 2; // 第二个月  
  
        // 计算每个月的兔子对数  
        for (int i = 3; i <= n; i++) {  
            dp[i] = dp[i - 1] + dp[i - 2]; // 递推公式  
        }  
  
        return dp[n]; // 返回第 n 个月的兔子对数  
    }  
  
    public static void main(String[] args) {  
        // 验证输出结果是否符合预期  
        System.out.println(solution(5) == 8);  
        System.out.println(solution(1) == 1);  
        System.out.println(solution(15) == 987);  
        System.out.println(solution(50) == 20365011074L); // 注意：Java中整数有范围限制，这里需要处理大数  
    }  
}

运行结果：

测试通过

提交失败！可以尝试改为python

完美整数

# 问题描述
一个整数如果由相同数字构成，可以称为完美整数；比如说1、11、333就是完美整数，12、19、101就是不完美的整数。
现在想知道，在区间 `[x, y]` 中有多少个整数是完美整数。

## 输入格式
每个样例有一行，是整数 `x` 和 `y`；（1 ≤ x ≤ y ≤ 10^9）

## 输出格式
每一个样例一行，是整数 `m`，表示区间 `[x, y]` 中有 m 个整数是完美整数。

## 输入样例1
1 10  

## 输出样例1

9  

## 输入样例2
2 22


## 输出样例2
10

## 数据范围

1 ≤ t ≤ 1000
1 ≤ x ≤ y ≤ 10^9

问题分析：

其实生成了10^9之内的所有完美整数，然后对这些完美整数进行排序，然后计算完美整数的左右区间，通过区间得到完美整数的数量

代码如下：

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

public class Main {
    // Generate all perfect numbers not exceeding 10^9
    public static List<Integer> generatePerfectNumbers() {
        List<Integer> perfectNumbers = new ArrayList<>();
        for (int digit = 1; digit <= 9; digit++) {  // From 1 to 9
            int perfectNumber = digit; // Use int instead of long
            while (perfectNumber <= 1000000000) {  // Build perfect numbers by concatenating
                perfectNumbers.add(perfectNumber);
                if (perfectNumber > 1000000000 / 10) break; // Prevent overflow when multiplying by 10
                perfectNumber = perfectNumber * 10 + digit;
            }
        }
        return perfectNumbers;
    }

    // Precompute perfect numbers
    static List<Integer> perfectNumbers = generatePerfectNumbers();

    public static int solution(int x, int y) {
        Collections.sort(perfectNumbers); // Sort perfect numbers
        int leftIndex = lowerBound(perfectNumbers, x);  // Find first position >= x
        int rightIndex = upperBound(perfectNumbers, y);  // Find first position > y
        // Count of perfect numbers in the range
        return rightIndex - leftIndex;  
    }

    public static int lowerBound(List<Integer> arr, int key) {
        int left = 0, right = arr.size();
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (arr.get(mid) < key) {
                left = mid + 1;
            } else {
                right = mid; // Include mid if it's equal
            }
        }
        return left;
    }

    public static int upperBound(List<Integer> arr, int key) {
        int left = 0, right = arr.size();
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (arr.get(mid) <= key) { // Increment for equal values
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        return left;
    }

    public static void main(String[] args) {
        System.out.println(solution(1, 10) == 9); // Should print true
        System.out.println(solution(2, 22) == 10); // Should print true
    }
}

运行结果：

找出整数数组中占比超过一半的数

## 问题描述
- 给定一个长度为n的整型数组，已知其中一个数字的出现次数超过数组长度的一半，找出这个元素

## 输入格式
- 一个长度为n的数组，其中某个元素的出现次数大于n/2

## 输出格式
- 一个整数

## 输入样例
- [1,3,8,2,3,1,3,3,3]

## 输出样例
- 3

## 数据范围
- 任意长度为n整数数组，其中某个元素的出现次数大于n/2

问题分析：

其实就是找出出现次数超过一半的数，首先通过快排将数组拍成有序的，然后取有序的中间那个数就可以，因为是大于一半的，就算是极限情况从头或者从尾开始，中间那个数也是出现一半以上的，更不用说其他在中间的情况了

代码如下：

import java.util.Arrays;

public class Main {
    // Correct quick sort function
    public static void quickSort(int l, int r, int[] num) {
        if (l >= r) return;
        int mid = num[(l + r) / 2]; // Choose pivot element
        int i = l - 1, j = r + 1;
        while (i < j) {
            do i++; while (num[i] < mid);
            do j--; while (num[j] > mid);
            if (i < j) {
                // Swap elements
                int temp = num[i];
                num[i] = num[j];
                num[j] = temp;
            }
        }
        quickSort(l, j, num);
        quickSort(j + 1, r, num);
    }

    // Modified solution function, returning the element that appears more than half the time
    public static int solution(int[] list) {
        quickSort(0, list.length - 1, list);
        return list[(list.length - 1) / 2]; // Return the median element
    }

    public static void main(String[] args) {
        // Test cases
        System.out.println(solution(new int[]{1, 3, 8, 2, 3, 1, 3, 3, 3}) == 3); // Should print true
    }
}

运行结果：

找出最长的神奇数列

# 问题描述

小明是一个中学生，今天他刚刚学习了数列。他在纸上写了一个长度为 `n` 的正整数序列，$a_0,a_1,\ldots,a_{n-1}$。这个数列里面只有 1 和 0，我们将 1 和 0 没有重复跟随并且至少由 3 个数组成的数列的数列称之为「神奇数列」。比如 `10101` 是一个神奇数列，`1011` 不是一个神奇数列。他想知道这个序列里面最长的「神奇数列」是哪个，你可以帮帮他吗？

## 输入格式

- 一行连续的数 `s`，只有 `0` 和 `1`

## 输出格式

- 一行数

## 输入样例


0101011101


## 输出样例


010101


## 数据范围

- $1 < s.length \leq 5 \times 10^4$

问题分析：

通过遍历字符串，如果相邻的不同，就长度增加，如果相同了，就把相同之前的不同的一个串尝试更新的最长神奇数列，首先要长度大于3，其次要和之前的生气数列比较，最后返回字符串

代码如下：

public class Main {
    public static String solution(String inp) {
        String maxList = ""; // To store the longest magical sequence
        int maxLength = 0; // Length of the longest magical sequence
        int n = inp.length(); // Length of the input string

        // Current magical sequence's starting position and length
        int start = 0;
        int currentLength = 1;

        for (int i = 1; i < n; i++) {
            if (inp.charAt(i) != inp.charAt(i - 1)) { // Current character differs from previous character
                currentLength++; // Update the length of the current magical sequence
            } else {
                // Check if the current length is at least 3, and update if necessary
                if (currentLength >= 3) {
                    String candidate = inp.substring(start, i);
                    if (currentLength > maxLength) {
                        maxLength = currentLength;
                        maxList = candidate; // Update the longest magical sequence
                    }
                }
                // Reset the current magical sequence
                start = i;
                currentLength = 1; // Reset counting
            }
        }

        // Handle the last segment of the magical sequence
        if (currentLength >= 3) {
            String candidate = inp.substring(start, n);
            if (currentLength > maxLength) {
                maxList = candidate; // Update the longest magical sequence
            }
        }

        return maxList; // Return the longest magical sequence
    }

    public static void main(String[] args) {
        // Add your test cases here
        System.out.println(solution("0101011101").equals("010101")); // Should print true
    }
}

运行结果：

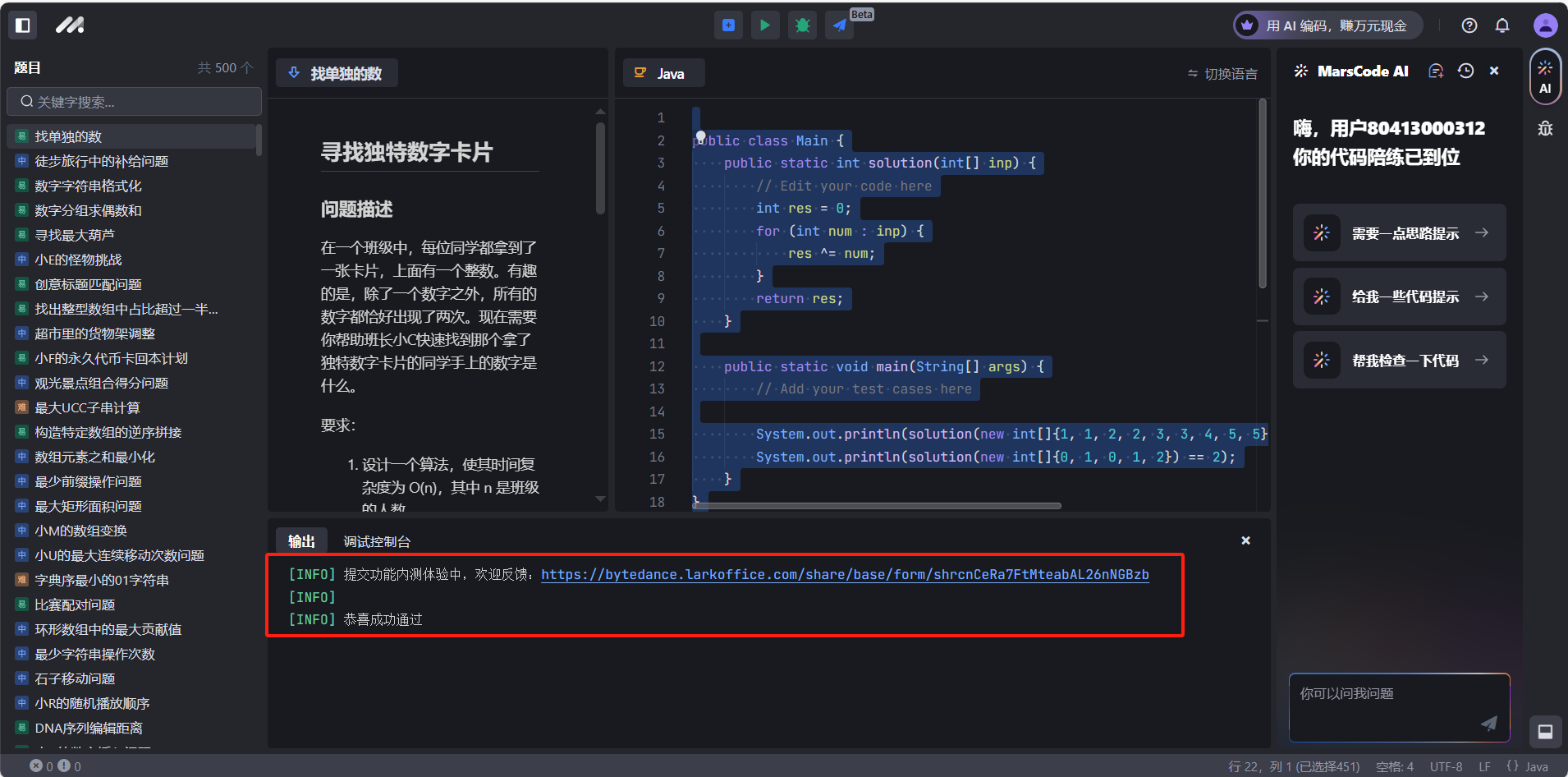
找单独的数

# 问题描述
有一堆数字，除了一个数字，其它的数字都是成对出现。班上的每个同学拿一个数字，正好将这些数字全部拿完，问如何快速找到拿了单独数字的同学？

## 输入格式
- 空格分隔输入所有的数字

## 输出格式
- 单独的那个数字

## 输入样例(1)
```
1 1 2 2 3 3 4 5 5
```
## 输出样例(1)
4

## 输入样例(2)
```
0 1 0 1 2
```
## 输出样例(2)
2

问题分析：

这个应该是100个题目中最简单的一个了，通过异或会把相同的数字抵消掉，剩下的就是那个单独的数字。

代码如下：


public class Main {
    public static int solution(int[] inp) {
        // Edit your code here
        int res = 0;
        for (int num : inp) {
            res ^= num;
        }
        return res;
    }

    public static void main(String[] args) {
        // Add your test cases here

        System.out.println(solution(new int[]{1, 1, 2, 2, 3, 3, 4, 5, 5}) == 4);
        System.out.println(solution(new int[]{0, 1, 0, 1, 2}) == 2);
    }
}

提交结果：

字符串最短循环字串

# 问题描述
- 输入一个字符串，判断其是否完全循环，若是循环的，输出最短的循环子串，否则输出空`""`
- 如输入 `abababab`，输出 `ab`；输入 `ab` 则输出 `""`

## 输入格式
- 合法字符串 如 `abcabcabcabc` `aaa`

## 输出格式
- 最短的循环子串 `"abc"` `"a"`

## 输入样例
- `"abcabcabcabc"`

## 输出样例
- `"abc"`

## 数据范围
测试数据集

问题分析：

首先将每一种可能的字符串切出来，然后通过循环比较，字串通过取余循环，来判断是否为循环字串，如果j走到了最后，那么当前的字串就是他的循环字串，因为是从小的串开始，如果j走到了最后那么就不会切更大的字串直接跳出循环，保证了是最小的字串，如果i走到最后还没有找到，那么结果就是“”。

代码如下：

public class Main {
    public static String solution(String inp) {
        int n = inp.length();
        for (int len = 1; len <= n / 2; len++) { // Check lengths from 1 to n / 2
            if (n % len == 0) { // Only consider lengths that divide the string length evenly
                String substring = inp.substring(0, len); // Get the potential repeating substring
                StringBuilder sb = new StringBuilder();

                // Build the string from repeating the substring
                for (int j = 0; j < n / len; j++) {
                    sb.append(substring);
                }

                // Check if the built string is equal to the original string
                if (sb.toString().equals(inp)) {
                    return substring; // Found the repeating substring
                }
            }
        }
        return ""; // If no substring found, return empty string
    }

    public static void main(String[] args) {
        // Add your test cases here
        System.out.println(solution("abcabcabcabc").equals("abc")); // Should print true
        System.out.println(solution("aaa").equals("a")); // Should print true
        System.out.println(solution("abababab").equals("ab")); // Should print true
        System.out.println(solution("ab").equals("")); // Should print true
        System.out.println(solution("abcdabcdabcdabcd").equals("abcd")); // Should print true
        System.out.println(solution("b").equals("")); // Should print true
    }
}

提交结果：

二进制反码转换问题

# 二进制反码转换问题
## 问题描述
小C在学习二进制运算，他了解到每个非负整数都有其二进制表示。例如，整数 5 可以被表示为二进制 "101"，整数 11 可以被表示为二进制 "1011"，并且除了 N = 0 外，任何二进制表示中都不含前导零。

二进制的反码表示是将每个 1 变为 0，每个 0 变为 1。例如，二进制数 "101" 的二进制反码为 "010"。现在小C想知道，给定一个十进制数 N，它的二进制反码对应的十进制数是多少。

## 测试样例
样例1：

输入：N = 5
输出：2

样例2：

输入：N = 10
输出：5

样例3：

输入：N = 0
输出：1

问题分析：

其实这是一刀特别简单的题目，第一步将十进制转换为二进制，第二部按位取反，第三步取反的二进制转换为十进制

代码如下：

public class Main {
    public static int solution(int N) {
        String binaryString = Integer.toBinaryString(N);
        //System.out.println(binaryString);
        StringBuilder binaryStringBuilder = new StringBuilder(binaryString);
        for (int i = 0; i < binaryStringBuilder.length(); i++) {
            if (binaryStringBuilder.charAt(i) == '1') {
                binaryStringBuilder.setCharAt(i, '0');
            } else {
                binaryStringBuilder.setCharAt(i, '1');
            }
        }
        //System.out.println(binaryStringBuilder);
        int result = Integer.parseInt(binaryStringBuilder.toString(), 2);
        return result;
    }  
  
    public static void main(String[] args) {  
        System.out.println(solution(5) == 2 ? "Pass" : "Fail"); // 输出 Pass  
        System.out.println(solution(10) == 5 ? "Pass" : "Fail"); // 输出 Pass  
        System.out.println(solution(0) == 1 ? "Pass" : "Fail"); // 输出 Pass  
    }  
}

中等题目

已完成 4

简单四则运算

# 问题描述

实现一个基本的计算器来计算一个简单的字符串表达式的值。注意事项如下：

- 输入是一个字符串表达式（可以假设所给定的表达式都是有效的）

- 字符串表达式可以包含的运算符号为：左括号 `(`, 右括号 `)`, 加号 `+`, 减号 `-`

- 可以包含的数字为：非负整数（< 10）

- 字符串中不包含空格

- 处理除法 case 的时候，可以直接省略小数部分结果，只保留整数部分参与后续运算

- 请不要使用内置的库函数 `eval`

## 输入格式

如：`3+4*5/(3+2)`

## 数据约束

见题目描述

## 输出格式

计算之后的数字

**输入样例**：
- `1+1`
- `3+4*5/(3+2)`
- `4+2*5-2/1`
- `(1+(4+5+2)-3)+(6+8)`

**输出样例**：
- `2`
- `7`
- `12`
- `23`

问题分析：

其实这是一道数据结构的题目，如果仔细学过数据结构或者考研考过，这是栈的应用，通过符号的优先级来确定入栈还是出栈，最后留在栈里的就是结果。

代码如下：

import java.util.*;
public class Main {
     // 返回运算符的优先级
     private static int precedence(char op) {
        if (op == '+' || op == '-') {
            return 1;
        }
        if (op == '*' || op == '/') {
            return 2;
        }
        return 0;
    }

    // 执行操作
    private static int applyOp(int a, int b, char op) {
        switch (op) {
            case '+': return a + b;
            case '-': return a - b;
            case '*': return a * b;
            case '/': return a / b; // 直接取整数部分结果
        }
        return 0;
    }

    // 计算表达式的值
    public static int solution(String tokens) {
        Stack<Integer> values = new Stack<>(); // 值栈
        Stack<Character> ops = new Stack<>(); // 运算符栈

        for (int i = 0; i < tokens.length(); i++) {
            // 跳过空格
            if (tokens.charAt(i) == ' ') {
                continue;
            }

            // 当前字符是数字，解析完整的数字
            if (Character.isDigit(tokens.charAt(i))) {
                int val = 0;
                while (i < tokens.length() && Character.isDigit(tokens.charAt(i))) {
                    val = (val * 10) + (tokens.charAt(i) - '0');
                    i++;
                }
                i--; // 补偿最后多加的一次递增
                values.push(val);
            } 
            // 当前字符是左括号，直接压入运算符栈
            else if (tokens.charAt(i) == '(') {
                ops.push(tokens.charAt(i));
            } 
            // 当前字符是右括号，处理栈中的运算符直到遇到左括号
            else if (tokens.charAt(i) == ')') {
                while (!ops.empty() && ops.peek() != '(') {
                    int val2 = values.pop();
                    int val1 = values.pop();
                    char op = ops.pop();
                    values.push(applyOp(val1, val2, op));
                }
                // 弹出左括号
                if (!ops.empty()) {
                    ops.pop();
                }
            } 
            // 当前字符是运算符
            else {
                while (!ops.empty() && precedence(ops.peek()) >= precedence(tokens.charAt(i))) {
                    int val2 = values.pop();
                    int val1 = values.pop();
                    char op = ops.pop();
                    values.push(applyOp(val1, val2, op));
                }
                ops.push(tokens.charAt(i));
            }
        }

        // 处理栈中剩余的运算符
        while (!ops.empty()) {
            int val2 = values.pop();
            int val1 = values.pop();
            char op = ops.pop();
            values.push(applyOp(val1, val2, op));
        }

        // 栈中应该只剩下一个值，即表达式的计算结果
        return values.pop();
    }

    public static void main(String[] args) {
        // 测试用例
        System.out.println(solution("1+1") == 2); // true
        System.out.println(solution("3+4*5/(3+2)") == 7); // true
        System.out.println(solution("4+2*5-2/1") == 12); // true
        System.out.println(solution("(1+(4+5+2)-3)+(6+8)") == 23); // true
    }
}

运行结果：

数字翻译成字符串有多少种可能性

# 问题描述

给定一个数字，我们按照如下规则把它翻译为字符串：0 翻译成 “a” ，1 翻译成 “b”，……，11 翻译成 “l”，……，25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数，用来计算一个数字有多少种不同的翻译方法。

## 输入格式

一个 `int` 型的数字，`0 <= num <= 2` 的 31 次方

## 输出格式

也是一个 `int` 型数字，代表字符串的总共可能性

**输入样例**

输入: 12258

**输出样例**

输出: 5

解释: 12258 有 5 种不同的翻译，分别是 "bccfi", "bwfi", "bczi", "mcfi" 和 "mzi"

问题分析：

要解决这个问题，即计算一个数字的不同翻译方法，实际上可以通过动态规划来实现。我们需要将输入数字看作一串字符，然后根据规则将其翻译成相应的字符串。

解决思路

动态规划：

我们定义一个动态规划数组 dp，其中 dp[i] 表示在前 i 个字符的翻译方案数量。

对于一个长度为 n 的字符串，我们考虑以下两种情况：

只将当前字符翻译成对应的字母。

将当前字符和前一个字符结合起来翻译（需要确保这两个字符组成的数字合法，且在 0 到 25 之间）。

状态转移方程：

dp[i] = dp[i - 1] 如果当前字符可以单独翻译（即非零）。

dp[i] += dp[i - 2] 如果前两个字符可以合并翻译（即它们组合成的数字在 10 到 25 之间）。

代码如下：

public class Main {
    public static int solution(int num) {
        String str = String.valueOf(num); // 将数字转成字符串
        int n = str.length();

        if (n == 0) return 0;
        if (n == 1) return 1; // 单字符的情况

        // 动态规划数组
        int[] dp = new int[n + 1];
        dp[0] = 1; // 空字符串一种方式
        dp[1] = 1; // 一个字符也有一种方式

        for (int i = 2; i <= n; i++) {
            // 只翻译当前字符
            dp[i] = dp[i - 1];

            // 结合前一个字符一起翻译
            int twoDigit = Integer.parseInt(str.substring(i - 2, i)); // 当前字符及前一个字符形成的数
            if (twoDigit >= 10 && twoDigit <= 25) {
                dp[i] += dp[i - 2]; // 如果能够组合翻译
            }
        }

        return dp[n]; // 返回总的翻译方式
    }

    public static void main(String[] args) {
        // You can add more test cases here
        System.out.println(solution(12258) == 5);
        System.out.println(solution(1400112) == 6);
        System.out.println(solution(2110101) == 10);
    }
}

运行结果：

最大异或和计算

# 最大异或和计算
## 问题描述
给定两个长度为 n 的数组 a 和 b，定义 f(c) 为数组 c 的所有元素的总和。现在，你需要恰好删除数组 a 或者数组 b 中的一个元素，使得 f(a) 和 f(b) 的异或结果最大。请输出这个最大的异或和。

## 测试样例
样例1：

输入：n = 3,a = [1, 2, 3],b = [3, 2, 1]
输出：5

样例2：

输入：n = 4,a = [4, 5, 6, 7],b = [7, 8, 9, 10]
输出：51

样例3：

输入：n = 5,a = [10, 20, 30, 40, 50],b = [50, 40, 30, 20, 10]
输出：248

问题分析：

第一步分别计算两个数组的总和，第二步遍历数组A，通过尝试删除每一个元素的数组A的和和数组B的和异或，然后通过迭代比较，获取最大值，第三步类似于第二步，只不过这一步遍历的是数组B，删除B的每一个元素。

总之，通过不断比较得出最大异或和的值

代码如下：

public class Main {
    public static int solution(int n, int[] a, int[] b) {
        // 计算数组 a 和 b 的总和
        int sumA = 0;
        int sumB = 0;

        for (int num : a) {
            sumA += num;
        }

        for (int num : b) {
            sumB += num;
        }

        int maxXor = 0;

        // 尝试删除数组 a 中的每一个元素
        for (int i = 0; i < n; i++) {
            int newSumA = sumA - a[i];
            int newSumB = sumB;
            maxXor = Math.max(maxXor, newSumA ^ newSumB);
        }

        // 尝试删除数组 b 中的每一个元素
        for (int i = 0; i < n; i++) {
            int newSumA = sumA;
            int newSumB = sumB - b[i];
            maxXor = Math.max(maxXor, newSumA ^ newSumB);
        }

        return maxXor;
    }

    public static void main(String[] args) {
        System.out.println(solution(3, new int[]{1, 2, 3}, new int[]{3, 2, 1}) == 5);
        System.out.println(solution(4, new int[]{4, 5, 6, 7}, new int[]{7, 8, 9, 10}) == 51);
        System.out.println(solution(5, new int[]{10, 20, 30, 40, 50}, new int[]{50, 40, 30, 20, 10}) == 248);
    }
}

提交结果：

五子棋获胜策略

# 问题描述
- 假设存在一个五子棋棋盘，大小未知。上面只摆放了一些白色的棋子，现在你的手中还有一个白色棋子，要求找出在棋盘的哪些位置摆放这个棋子，能够使棋盘上出现五颗棋子连成一线。
- 备注：棋盘上当前不存在连成一条线的五个棋子，但至少存在一个点能够凑出五子一线（不限于横、竖、斜线）

## 输入格式
- 第一行输入一个正整数 `n`，表示棋盘的宽度，棋盘总共可以容纳 `n^2` 个棋子。
- 第 2 到 `n+1` 行输入 `n` 个数字。每次输入 `n` 个数，其中 `1` 代表有棋子，`0` 代表没有棋子。

## 输出格式
- 如果有 `n` 个可放置点，输出 `n` 行。
- 每行输出两个数字，以空格分隔，分别代表放置点在棋盘上的行数和列数。
- 输出顺序需要按照行数从小到大、列数从小到大的顺序。

## 输入样例
```
6  
0 0 0 0 0 0  
0 1 0 0 0 0  
0 0 1 0 0 0  
0 0 0 1 0 0  
0 0 0 0 1 0  
0 0 0 0 0 0  
```


## 输出样例

1 1
6 6


## 数据范围
- 第一行中，棋盘宽度为 `[1, 10)` 中的整数。
- 第 2 到 `n+1` 行中，只会出现 `0` 或 `1`。

问题分析：

这个题目跟我之前做过的一个题目很像，那个是动态的，双方互相落子判断谁胜利，这个是给你一个棋局，没有黑白方，判断落子胜利有几种方式，原理就是落子时，判断上下左右左斜右斜，且在规定范围内，是否可以达到五子连珠。

代码如下：

import java.util.ArrayList;
import java.util.List;
public class Main {
    // 检查某个位置是否可以形成五子连线
    public static boolean canFormLine(int x, int y, int[][] board, int n) {
        // 定义四个方向：右，下，右下，左下
        int[][] directions = {{1, 0}, {0, 1}, {1, 1}, {1, -1}};

        for (int[] dir : directions) {
            int count = 1; // 当前位置记为1
            int dx = dir[0], dy = dir[1];

            // 检查正向
            for (int step = 1; step < 5; ++step) {
                int nx = x + dx * step;
                int ny = y + dy * step;
                if (nx >= 0 && nx < n && ny >= 0 && ny < n && board[nx][ny] == 1) {
                    count++;
                } else {
                    break;
                }
            }

            // 检查反向
            for (int step = 1; step < 5; ++step) {
                int nx = x - dx * step;
                int ny = y - dy * step;
                if (nx >= 0 && nx < n && ny >= 0 && ny < n && board[nx][ny] == 1) {
                    count++;
                } else {
                    break;
                }
            }

            // 如果形成五子连接，则返回 true
            if (count >= 5) return true;
        }

        return false; // 没有符合条件的连线
    }

    // 主解决方案函数
    public static int[][] solution(int n, int[][] board) {
        List<int[]> results = new ArrayList<>();

        // 检查每个位置是否能放置新棋子形成五子连线
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (board[i][j] == 0) { // 只检查空位
                    if (canFormLine(i, j, board, n)) {
                        results.add(new int[]{i + 1, j + 1}); // 记录行列，+1因要求从1开始
                    }
                }
            }
        }

        // 将结果转换为二维数组
        int[][] resultArray = new int[results.size()][2];
        for (int i = 0; i < results.size(); i++) {
            resultArray[i] = results.get(i);
        }

        return resultArray.length > 0 ? resultArray : new int[][]{{-1, -1}}; // 如果没有结果，返回 {-1, -1}
    }

    public static void main(String[] args) {
        // 测试用例
        int[][] array = {
            {0, 0, 0, 0, 0, 0},
            {0, 1, 0, 0, 0, 0},
            {0, 0, 1, 0, 0, 0},
            {0, 0, 0, 1, 0, 0},
            {0, 0, 0, 0, 1, 0},
            {0, 0, 0, 0, 0, 0}
        };

        int[][] expectedOutput = {{1, 1}, {6, 6}};
        System.out.println(java.util.Arrays.deepEquals(solution(6, array), expectedOutput)); // 验证测试结果
    }
}

运行结果：

困难题目

已完成 2

二进制之和

# 问题描述

给定两个二进制字符串，返回他们的和（用十进制字符串表示）。输入为非空字符串且只包含数字 1 和 0 ，请考虑大数问题。时间复杂度不要超过 O(n^2)，其中 n 是二进制的最大长度。

## 输入格式

每个样例只有一行，两个二进制字符串以英文逗号“,”分割

## 输出格式

输出十进制格式的两个二进制的和

**输入样例**：

101,110

**输出样例**：

11

**数据范围**：

每个二进制不超过 100 个字符，JavaScript 语言下请考虑大数的情况。

问题分析：

函数签名：

- string addBinary(const string &a, const string &b)：这个函数接收两个二进制字符串，并返回它们的十进制和作为字符串。

变量初始化：

- string result;：用于存储二进制加法的中间和最终结果（在反转之前）。
- int carry = 0;：初始化进位为0。
- int i = a.size() - 1; 和 int j = b.size() - 1;：分别初始化两个字符串的索引，从末尾开始遍历。

循环逻辑：

- while (i >= 0 || j >= 0 || carry)：当任一字符串还有未处理的位或存在进位时，继续循环。
- 在循环内部，首先处理进位，然后根据索引 i 和 j 的有效性，将对应位置的字符转换为数字并加到 sum 上。
- 更新进位 carry 和结果字符串 result。

结果处理：

- reverse(result.begin(), result.end());：由于是从字符串末尾开始构建结果，因此最后需要反转字符串。
- long long decimalSum = stoll(result, 0, 2);：将二进制字符串转换为十进制长整数。这一步实际上是多余的，因为题目要求返回的是十进制字符串，而不是长整数。
- return to_string(decimalSum);：将十进制长整数转换回字符串并返回。由于前面的 stoll 转换是多余的，这一步也可以优化为直接返回 result 字符串（在反转之后）。

代码如下：

public class Main {
   // 函数用于二进制字符串的加法
   public static String solution(String a, String b) {
    StringBuilder result = new StringBuilder();
    int carry = 0;  // 进位
    int i = a.length() - 1; // 指向a字符串的最后一个字符
    int j = b.length() - 1; // 指向b字符串的最后一个字符

    // 处理加法直到两个字符串都结束并且没有进位
    while (i >= 0 || j >= 0 || carry != 0) {
        int sum = carry; // 先将进位加上

        // 将字符转换为数字并加到sum中
        if (i >= 0) {
            sum += a.charAt(i) - '0'; 
            i--;
        }
        if (j >= 0) {
            sum += b.charAt(j) - '0'; 
            j--;
        }

        carry = sum / 2; // 计算新的进位
        result.append(sum % 2); // 结果取余，存入结果中
    }

    result.reverse(); // 反转结果
    long decimalSum = Long.parseLong(result.toString(), 2); // 转换为十进制
    return Long.toString(decimalSum); // 返回十进制字符串
}

public static void main(String[] args) {
    // 测试用例
    System.out.println(solution("101", "110").equals("11")); // true
    System.out.println(solution("111111", "10100").equals("83")); // true
    System.out.println(solution("111010101001001011", "100010101001").equals("242420")); // true
    System.out.println(solution("111010101001011", "10010101001").equals("31220")); // true
}
}

运行结果：

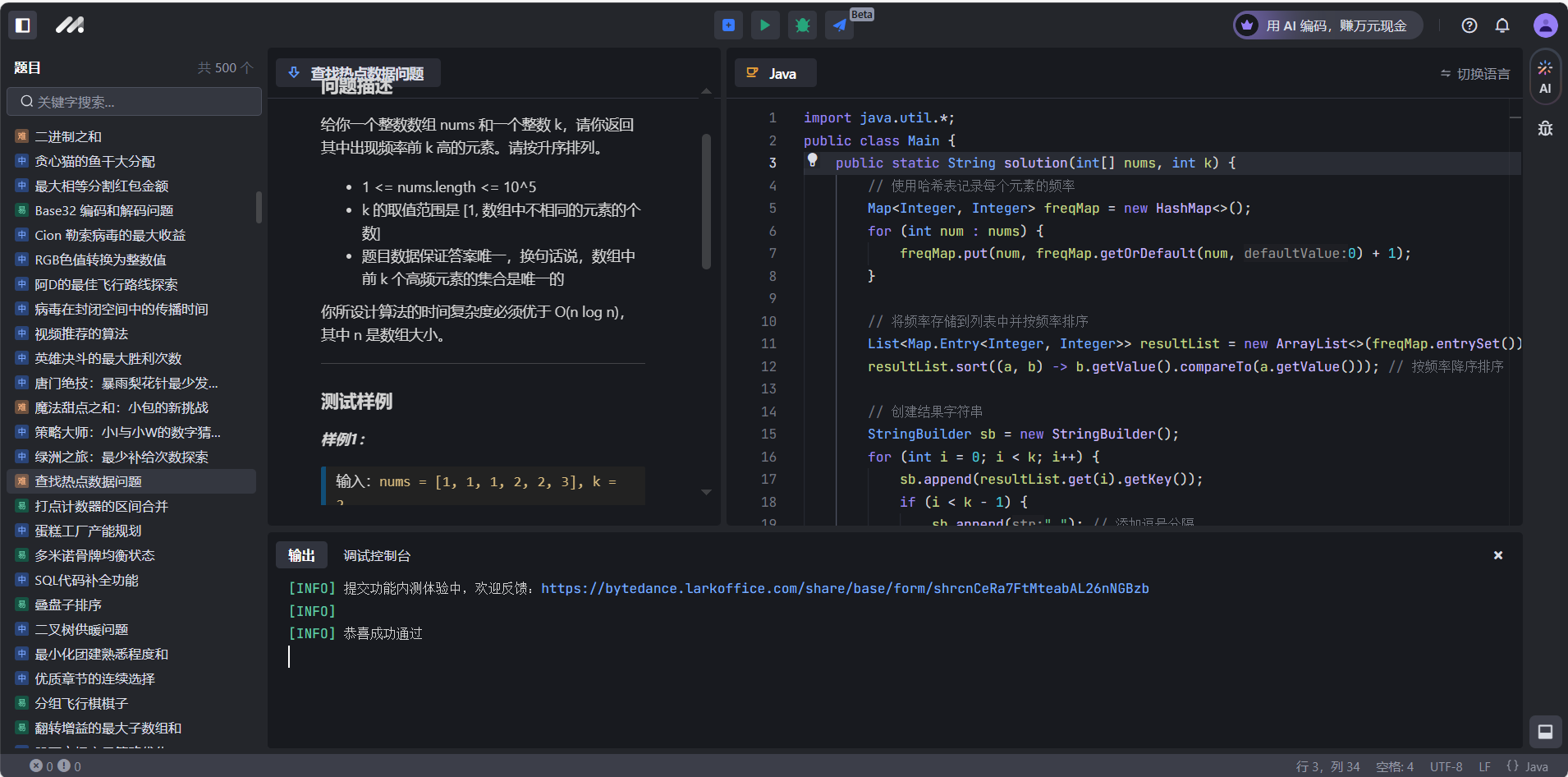
查找热点数据

# 问题描述

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按任意顺序返回答案。

- 1 <= nums.length <= 10^5
- k 的取值范围是 [1, 数组中不相同的元素的个数]
- 题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的

你所设计算法的时间复杂度必须优于 O(n log n) ，其中 n 是数组大小。

**示例 1**

输入: nums = [1,1,1,2,2,3], k = 2

输出: [1,2]

**示例 2**

输入: nums = [1], k = 1

输出: [1]

问题分析：

参数:

- vector<int>& nums: 输入的整数数组。
- int k: 需要返回的前k个高频元素的数量。

局部变量:

- unordered_map<int, int> freqMap: 用于存储每个数字的频率。
- vector<pair<int,int>> result: 存储哈希表中的键值对（数字及其频率）。
- stringstream ss: 用于构建最终返回的字符串。

逻辑流程:

- 构建频率映射: 遍历输入数组 nums，使用 unordered_map 记录每个数字的频率。
- 存储映射到结果向量: 将 freqMap 中的每个键值对（数字及其频率）添加到 result 向量中。
- 排序: 使用 sort 函数对 result 向量进行排序，排序依据是元素的频率（降序）。
- 构建返回字符串: 遍历排序后的 result 向量的前 k 个元素，将它们转换为字符串并使用逗号分隔，存储在 stringstream 中。
- 返回结果: 将 stringstream 中的内容转换为字符串并返回。

代码如下：

import java.util.*;
public class Main {
    public static String solution(int[] nums, int k) {
        // 使用哈希表记录每个元素的频率
        Map<Integer, Integer> freqMap = new HashMap<>();
        for (int num : nums) {
            freqMap.put(num, freqMap.getOrDefault(num, 0) + 1);
        }

        // 将频率存储到列表中并按频率排序
        List<Map.Entry<Integer, Integer>> resultList = new ArrayList<>(freqMap.entrySet());
        resultList.sort((a, b) -> b.getValue().compareTo(a.getValue())); // 按频率降序排序

        // 创建结果字符串
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < k; i++) {
            sb.append(resultList.get(i).getKey());
            if (i < k - 1) {
                sb.append(","); // 添加逗号分隔
            }
        }

        return sb.toString(); // 返回结果字符串
    }

    public static void main(String[] args) {
        // 测试用例
        int[] nums1 = {1, 1, 1, 2, 2, 3};
        int[] nums2 = {1};

        // 输出结果是否与预期相符
        System.out.println(solution(nums1, 2).equals("1,2")); // true
        System.out.println(solution(nums2, 1).equals("1")); // true
    }
}

运行结果：