快速排序（Quicksort）是一种高效的排序算法，最早由Tony Hoare在1960年提出。它采用了分治（Divide and Conquer）策略，平均时间复杂度为 $O(n\log n)$，在大多数实际应用中，表现优于其他 $O(n\log n)$ 的排序算法如归并排序（Merge Sort）。

基本原理

快速排序的核心思想是通过递归地将数组划分为两个子数组来实现排序，步骤如下：

1. 选择基准（Pivot）： 从数组中选择一个基准元素，可以是第一个、最后一个、中间一个或者随机一个。
2. 分区（Partition）： 将数组中的其他元素与基准进行比较，所有小于基准的元素移到基准的左边，大于基准的元素移到右边。
3. 递归排序： 递归地对左边和右边的子数组进行相同的操作，直到子数组的大小为1或者0，即数组已经有序。

原理模拟

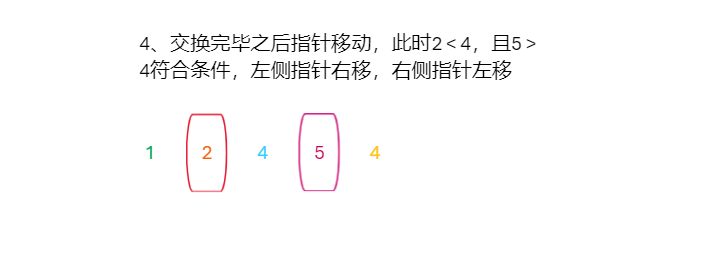
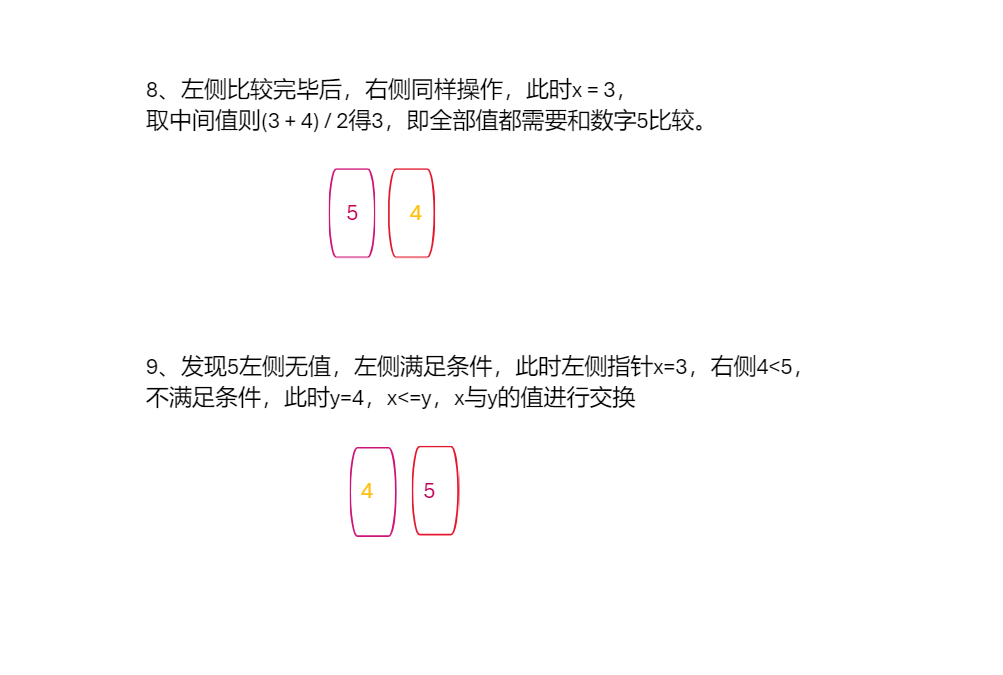
代码实现

以下是一个典型的C++实现：

void quickSort(int l, int r)
{
    int x = l, y = r, mid = arr[(r + l) / 2];
    while (x < y)
    {
        while (arr[x] < mid) x++;
        while (arr[y] > mid) y--;
        if (x <= y)
        {
            swap(arr[x], arr[y]);
            x++;
            y--;
        }
    }
    if (y > l) quickSort(l, y);
    if (x < r) quickSort(x, r);
}

代码解析：

1. 选择基准： 代码中 mid = arr[(r + l) / 2] 选择数组中间的元素作为基准。
2. 分区操作： 通过 while (arr[x] < mid) 和 while (arr[y] > mid) 找到左右两边需要交换的元素并进行交换。
3. 递归调用： 最后递归地对左右子数组继续进行快速排序。

实战应用

快速排序广泛应用于以下场景：

1. 大数据排序： 快速排序由于其优秀的平均时间复杂度，适合用于处理大型数据集。
2. 数据库索引排序： 数据库系统中经常使用快速排序来优化查询性能，特别是在索引的创建和维护过程中。
3. 编程竞赛和面试： 作为经典的排序算法，快速排序经常出现在各种编程竞赛和技术面试中。

快速排序的复杂度分析

1. 平均时间复杂度： 快速排序的平均时间复杂度是 $O(n\log n)$，这是在划分较为均匀的情况下，递归深度为 $\log n$，每次划分的操作需要线性时间 $O(n)$。
2. 最坏时间复杂度： 最坏情况下，快速排序的时间复杂度为 $O(n^2)$，比如当数组已经有序时，每次选择的基准都位于数组的一端。
3. 空间复杂度： 快速排序是就地排序算法（in-place），不需要额外的存储空间，空间复杂度取决于递归的深度。在最优情况下为 $O(\log n)$，最坏情况下为 $O(n)$。

快速排序的优化策略

1. 三数取中法： 在基准选择上可以采用首、尾和中间元素的中位数作为基准，能够有效降低最坏情况的概率。
2. 随机基准法： 随机选择基准可以避免输入数据的特殊排列导致最坏情况。
3. 小数组优化： 当数组较小时（如小于10个元素），使用插入排序等简单排序算法往往更加高效。

结论

快速排序由于其高效性和较低的空间占用，是非常实用的排序算法。通过对基准选择和递归策略的优化，可以有效避免最坏情况的发生，从而进一步提升其性能。在大数据处理、系统应用和竞赛中，快速排序都是一种值得选择的排序方案。