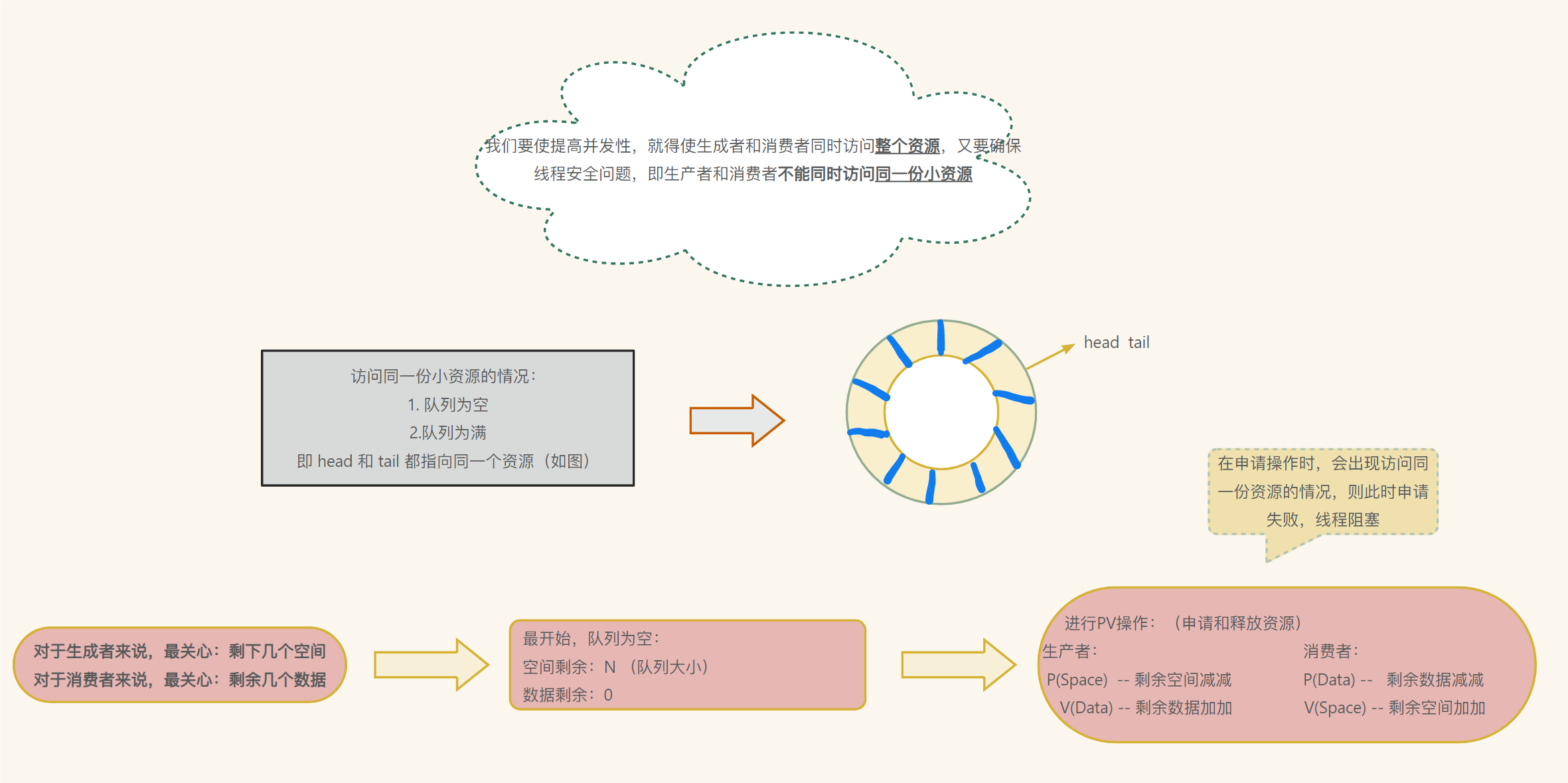
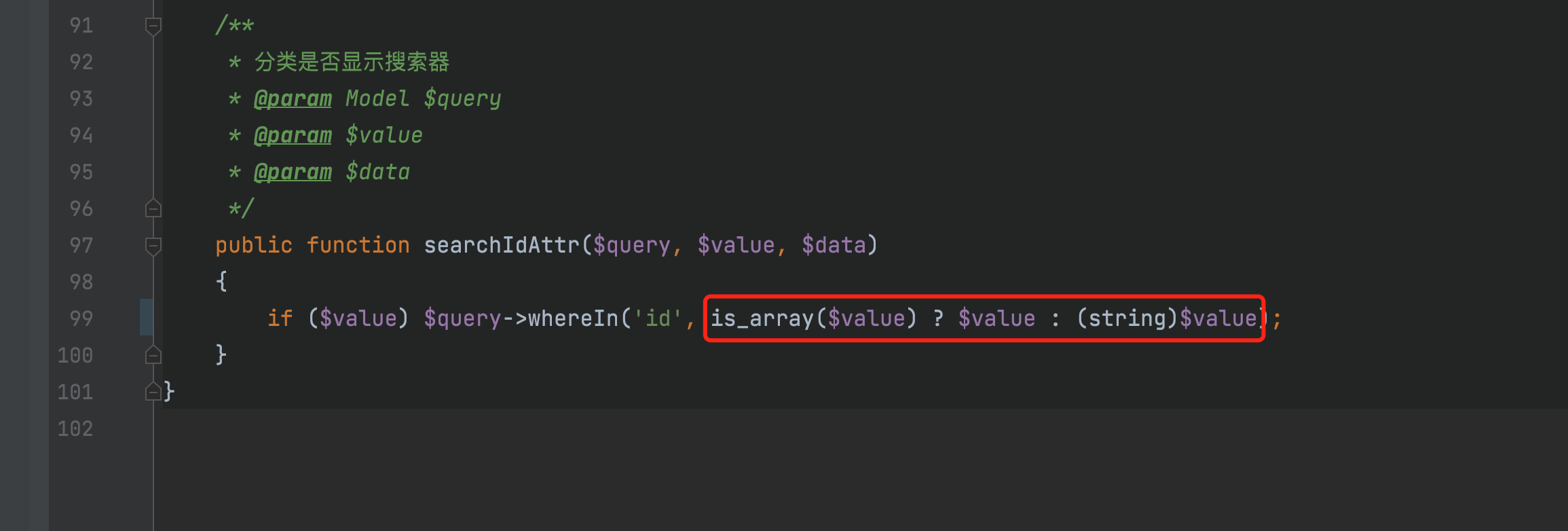
推荐文章
[凸优化-凸共轭]Legendre and Legendre-Fenchel transforms - 知乎 (zhihu.com)
一、Legendre变换
1、几何解释1
Legendre 变换通过选择斜率 作为新的自变量,将函数描述为它的斜率与相应的 x 的函数值之间的关系。几何上,它可以理解为用函数的斜率信息重新描述该函数,极大地拓展了我们在不同变量下描述物理系统的能力。
假设凸函数的Legendre 变换为
,则
的定义域为
的斜率的取值范围,
的取值为
中斜率为
的点的函数值。对于凸函数
,
中包含的
的所有信息。
2、数学推导
和
是凸函数。
一维情况下的推导 和 多维情况下的推导


3、几何解释2
这部分来看一下Legendre变换后的函数在几何上于原函数的关系:
,画在图像上:

公式中的等于图中的
,公式中的
等于图中的
,所以公式中的
等于图中的
即函数切线的负截距。
所以有以下几何解释:
Legendre 变换本质上是将一个曲线的点用该点上的切线表示。换句话说,你将函数的点集换成斜率 和切线的截距(由
表示)。也就是从一个点集转化为了一个“切线集”,点集中的每个点都包含两个信息:x和y,“切线集”中的每个切线也都包含两个信息:斜率和负截距。
反向推导:
对于,其在某点
处的切线方程为
切线方程的斜率为,负截距为
即
4、Legendre 变换的Legendre 变换是函数本身
数学推导

几何直观
上一点
处的切线为:
上一点
处的切线为:
所以他们是Legendre 变换是相互的。
也就是说的切线的斜率为自变量,负截距为函数值组成的函数
,
的切线的斜率和负截距分别是
和
。
5、从Legendre 变换函数到原函数的几何直观
对于一个凸且光滑的函数,在每个点处,有且仅有一个切线与之对应, 而这个切线又可以由
中唯一的一个点来表示,所以
与
是唯一对应的,他们相互包含着对方的所有信息。那么如何从
得到
呢?当然可以使用解析的方法,即对
进行Legendre 变换得到
。那么这个过程如何从几何视角来理解呢?
当从到
的变换过程中,
中的每个点都是
中相应点的切线信息,那么通过
即可画出
的所有切线,如图:

当画出所有切线时,在切线的上方将会形成一个保包络,这个包络即是。
同样的,由于与
是相对的,用
上的每个点画出
的所有切线时,切线上的包络也是
的图像。
二、共轭函数
1、定义及理解
了解了Legendre变换后,我们知道,存在Legendre变换的条件是它可微且是凸函数。对于是否可微,暂且不做讨论。想象一下,当
不是凸函数时,那么仍的Legendre变换,将会出现什么。
显然,其Legendre变换将会出现一对多的情况,这时取函数值的最大值,即此时Legendre变换的结果
即是
的共轭函数:
对于这个函数,自变量是的切线的斜率,因变量是切线负截距的最大值。
2、几何直观理解非凸函数的共轭函数
对于凸函数,其共轭函数就是其Legendre变换,共轭函数上的每个点对于原函数的每个点,即共轭函数包含原函数的所有信息,对于非凸函数,共轭函数上的每个点与原函数的对应关系是怎样的呢?从定义可以得知,非凸函数的Legendre变换会出现多对一的情况,共轭函数是取函数值的最大值,所以原非凸函数就会有一些点的信息丢失,不会传递到共轭函数,即存在斜率重复的一部分点的信息会丢失。

如图,红色部分的信息将会丢失,不会传递到共轭函数。
同样的,当对共轭函数再做Legendre变换时也不会再出现原函数中的红色段,得到的是边缘的两段函数,断点处直接直线连接。即当原函数不是凸函数时,其共轭函数的共轭函数不再是它本身。
三、Legendre变换与共轭函数的关系
从上面的分析已经可以得出Legendre变换与共轭函数的关系,即
当原函数是凸函数时,其Legendre变换就是其共轭函数;当原函数不是凸函数时,其不再符合Legendre变换的条件,当仍要对其做Legendre变换并取函数值的上确界时,得到的就是非凸函数的共轭函数。
四、对偶
1、Legendre 变换在对偶空间中的解释
Legendre 变换可以看作是将一个函数的表示从原空间映射到对偶空间。这意味着我们将一个函数的输入变量从原空间的变量 x 转换为对偶空间的变量 p(导数),并且通过这种转换构造了一个新函数,这个新函数描述的是原空间中的几何结构在对偶空间中的表现。
Legendre 变换将原始函数 f(x) 中的所有信息通过导数 p 转换到对偶空间 p-空间,描述了在对偶空间中的最大线性泛函形式。也就是说,Legendre 变换在对偶空间中找到了与原空间中曲线 f(x) 对应的线性表示。
2、共轭函数在对偶空间中的解释
共轭函数通过将原函数 f(x) 中的点和切线信息映射到对偶空间 p,从而给出原函数在对偶空间中所有可能的线性映射。这就意味着,我们不再直接处理原空间中的点,而是处理这些点的“线性效应”,这体现了对偶空间中的信息。