前言
状态是什么?状态就是数据,准确点说,状态是指 Flink 作业计算时依赖的历史数据或中间数据。如果一个 Flink 作业计算依赖状态,那它就是有状态计算的作业,反之就是无状态计算的作业。
举个例子,服务端应用为了方便扩缩容,一般会设计成无状态的,但是对外服务的接口又是有状态的,这是因为服务端应用本身不存储数据,数据存储在关系型或非关系型数据库中,此时的“状态”就从服务端迁移到数据库中了。
Flink 同理,一个稍微复杂一点的作业,基本都会使用到状态。Flink 作为一款强大的开源流处理框架,以其卓越的性能和丰富的功能备受瞩目,如何实现状态的高效访问和容错恢复,是 Flink 不得不解决的问题。
Flink有状态计算方案
Flink 是不是也可以效仿服务端应用,把状态数据存储在数据库中呢?这么做当然可以,但是会存在以下几个问题:
- 数据库种类这么多,Flink 难以适配所有数据库,且容错恢复的成本很高
- 开发者使用状态,必须了解状态存储的细节,使用门槛较高
- 状态访问难以形成统一的接口,徒增使用门槛
- 数据库的访问性能会增加 Flink 作业的延迟
以上这些问题里,最最重要的是性能问题。在大数据流处理场景中,处理的数据量是非常庞大的,单单是动辄几十万甚至百万的TPS,就不是传统数据库能承受的,况且还要考虑到Flink和数据库交互产生网络IO的额外开销。
基于这些问题,Flink 自己实现了一套状态的访问和存储方案:
- 状态本地化 如果Flink通过网络去访问状态,必然会导致较高的延迟和低吞吐问题。Flink 直接状态本地化,将状态存储在subTask本地内存或磁盘上,这样就可以将状态的访问耗时从毫秒级直接优化到微妙甚至纳秒级,实现状态的极致访问速度。
- 一致性快照实现容错 传统的有状态计算方案,为了实现异常容错时的数据处理和状态结果满足精准一次的一致性要求,往往会使用事务机制,大大增加用户的开发成本。Flink 自身实现了状态一致性的异常容错的逻辑,用户无需参与。Flink 以 Chandy-Lamport 分布式系统快照算法作为理论基础,实现了名为 Checkpoint 的分布式轻量级异步快照,保证了精确一次的数据处理和一致性状态,数据既不会多算,也不会少算。
- 统一的状态访问接口 Flink提供了一套统一的状态访问接口,用户基于这套接口,不但能享受状态本地化带来的极致的访问速度,还够得到状态持久化和一致性快照带来的异常容错场景下精确一次的数据处理保证。
状态接口
Flink 状态的顶层接口是org.apache.flink.api.common.state.State,基于此派生出五个常用的子接口。
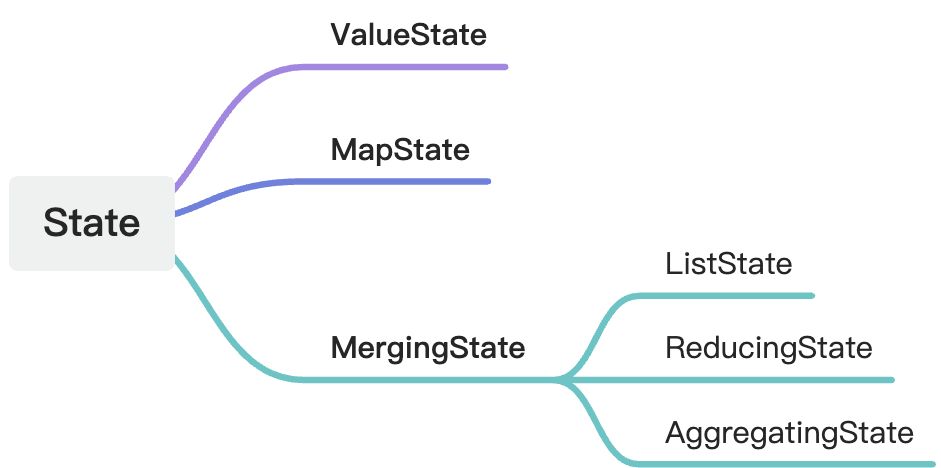
- ValueState 用于存储单个值的状态接口
- MapState 用于存储键值对的状态接口
- ListState 用于存储列表值的状态接口
- ReducingState 用于存储归约状态的接口,添加进去的状态会先经过ReduceFunction和旧值进行归约计算并保存
- AggregatingState 用于存储归约状态的接口,添加进去的状态会先经过AggregateFunction和旧值进行归约计算并保存,和ReducingState的区别是中间数据可以和输入数据类型不一致
键值状态和算子状态
Flink 将状态是否要根据Key分组,将状态划分为 **键值状态(Keyed State)和算子状态(Operator State)**两类。
键值状态只能在 KeyedStream 上使用,数据先经过 keyBy 分组,相同key的数据共享同一个键值状态。算子状态的作用范围是当前subTask,同一个subTask共享同一个算子状态。另外,键值状态支持的状态类型更丰富,算子状态只支持 ListState 状态类型,这主要是为了算子并行度发生变化时方便状态的重分配。
要想使用算子状态,只需要在 KeyedStream 上应用 ProcessFunction,通过RuntimeContext 获取状态对象来访问状态即可。
keyedStream.process(new ProcessFunction<Integer, Integer>() {
ValueState<Integer> sumState;
@Override
public void open(Configuration parameters) throws Exception {
// 获取状态对象
sumState = getRuntimeContext().getState(new ValueStateDescriptor<Integer>("sum", Integer.class));
}
@Override
public void processElement(Integer value, ProcessFunction<Integer, Integer>.Context context, Collector<Integer> collector) throws Exception {
sumState.value();// 访问状态
sumState.update();// 更新状态
}
})
算子状态可以在任意算子中使用,但是被限制只能用 ListState 状态类型。要使用算子状态,要实现 CheckpointedFunction 接口,通过重写 initializeState() 来恢复算子状态,重写 snapshotState() 在执行快照时存储状态。
public class MyProcess implements CheckpointedFunction {
ListState<Integer> listState;
@Override
public void snapshotState(FunctionSnapshotContext functionSnapshotContext) throws Exception {
// 执行快照,存储状态
listState.add();
}
@Override
public void initializeState(FunctionInitializationContext functionInitializationContext) throws Exception {
listState = functionInitializationContext.getOperatorStateStore().getListState(
new ListStateDescriptor<Integer>("elements", Integer.class)
);
// 从异常中恢复状态
if (functionInitializationContext.isRestored()) {
Iterator<Integer> iterator = listState.get().iterator();
while (iterator.hasNext()) {
iterator.next();
}
}
}
}
状态后端
Flink 状态本地化后,状态直接存储在subTask内存或本地磁盘中,避免了通过网络来访问状态,实现了极致的访问速度。但是随之而来的问题就是,subTask 崩溃后的数据容错和恢复。Flink 基于 Chandy-Lamport 分布式系统快照算法实现了名为 Checkpoint 的分布式轻量级异步快照,Flink 会周期性的触发 Checkpoint 操作,将subTask本地的状态数据持久化到远程分布式文件系统中,这个部分被 Flink 设计成可插拔的组件:后端组件(State Backend)。
下面是 Flink 支持的几种常用 State Backend:
- HashMapStateBackend 底层使用哈希表将状态数据存储在subTask内存中,状态的访问效率特别高,但是受限于机器自身的内存限制,存储的状态数据量有限。
- EmbeddedRocksDBStateBackend 将状态数据存储到内嵌的 RocksDB 数据库中,RocksDB是Facebook基于levelDB使用C编写的嵌入式K-V存储引擎,因为数据是保存在磁盘上的,它的状态访问性能虽然不如HashMapStateBackend,但它的存储能力是惊人的,甚至可以达到TB级别,非常适合处理大状态、长窗口的有状态计算作业,Checkpoint 时将数据快照写入远程分布式文件系统。
- FsStateBackend 基于文件系统的状态后端,subTask将数据存储在内存中,Checkpoint 时将数据快照写入远程分布式文件系统。
以 FsStateBackend 为例,在作业中指定状态后端的示例代码如下:
StreamExecutionEnvironment environment = StreamExecutionEnvironment.getExecutionEnvironment();
// Checkpoint频率
environment.enableCheckpointing(1000, CheckpointingMode.EXACTLY_ONCE);
environment.getCheckpointConfig().enableExternalizedCheckpoints(CheckpointConfig.ExternalizedCheckpointCleanup.RETAIN_ON_CANCELLATION);
// 状态后端配置
environment.setStateBackend(new FsStateBackend("file:///Users/panchanghe/temp/flink/state"));
尾巴
Flink 提供了一套统一且易用的状态接口API,基于这套接口开发者可以方便地开发出一个精准处理一次的有状态计算作业。Flink 通过将状态本地化,实现了极致的状态访问速度,避免了通过网络访问状态数据导致的高延时和低吞吐的问题。为了实现数据的精准一次处理,保证数据的不多算也不少算,Flink 实现了 Checkpoint 轻量级分布式快照算法,通过定时把subTask本地的状态数据持久化到远程的分布式文件系统来实现异常容错恢复。