题目

题目大意

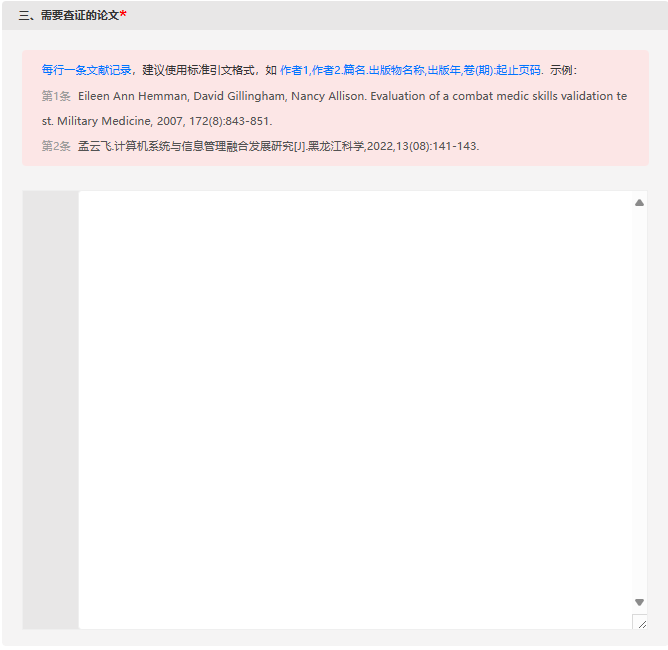
给出n个城市的连通图，其中共有m条边，起点为C1，终点为C2。每个城市都有一定数目的救援队，现从C1出发，每经过一个城市，都可以加上这个城市的救援队。要求从C1到C2最短路径的个数，并输出最短路径中最大的救援队数量。

思路

固定源点求最短路径，用迪杰斯特拉算法。该题又多了两个要求，一个是最短路径的数目，另一个是最大救援队的数目。迪杰斯特拉算法中用到3个数组，分别是bool类型的b数组，判断各节点是否被访问过；path数组，存储最短路径的长度；temp数组，存储临时的路径长度。所以还需要再加上num数组，求最短路径的个数；res数组，存储最大救援队的数目。这两个数组可以参与到temp数组的更新中。

多个最短路径：如果temp[i] == temp[now] + g[now][i]，说明找到了另外一条最短路径，num[i] += num[now]，累加。还要更新救援队数目，取两者中最大的，res[i] = max(res[i], res[now] + rescue[i])。如果当前只有一个最短路径，正常更新就可以。

需要注意，初始化图时，自己和自己是连通的，距离为0；num[C1]要初始化为1，自己到自己有一条路径，后续更新路径时，有重复路径累加，没有就继承。

知识点

num.resize(n, 0);  // 初始化vector数组的大小和元素值

代码

#include <iostream>
#include <vector>
#include <climits>
#include <cmath>
using namespace std;

int n, m, c1, c2;
int g[501][501] = {0};
vector<int> rescue;  // 各城市救援队的数目
vector<int> path;  // 记录最短路径的长度
vector<bool> b;  // 标记是否被访问过
vector<int> temp;  // 存放目前的路径长度
vector<int> num;  // 到达每个节点的最短路径的数量
vector<int> res;  // 记录最大救援队数

void dijie(int start){
    temp[start] = 0;
    path[start] = 0;
    res[start] = rescue[start];
    num[start] = 1;  // 自己到自己的路径只有一条

    for (int count = 0; count < n; count++) {
        int now = -1, minl = INT_MAX;
        // 找到当前未访问的节点中，距离最小的节点
        for (int i = 0; i < n; i++) {
            if (!b[i] && temp[i] < minl) {
                minl = temp[i];
                now = i;
            }
        }
        if (now == -1) break;  // 如果未找到合适的节点，说明所有节点已访问
        b[now] = true;

        // 更新邻接节点的距离
        for (int i = 0; i < n; i++) {
            if (!b[i] && g[now][i] < INT_MAX) {  // 如果 i 节点未访问并且与 now 有边
                if (temp[i] > temp[now] + g[now][i]) {
                    // 找到更短路径
                    temp[i] = temp[now] + g[now][i];
                    path[i] = temp[i];
                    num[i] = num[now];  // 更新最短路径的数量
                    res[i] = res[now] + rescue[i];  // 更新最大救援队数量
                } else if (temp[i] == temp[now] + g[now][i]) {
                    // 找到相同长度的最短路径
                    num[i] += num[now];
                    res[i] = max(res[i], res[now] + rescue[i]);  // 更新救援队数量
                }
            }
        }
    }
}

int main() {
    cin >> n >> m >> c1 >> c2;
    rescue.resize(n);
    for (int i = 0; i < n; i++) {
        cin >> rescue[i];
    }

    // 初始化图
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            g[i][j] = (i == j ? 0 : INT_MAX);  // 初始化自己到自己为 0，其他为无穷大
        }
    }
    for (int i = 0; i < m; i++) {
        int v1, v2, w;
        cin >> v1 >> v2 >> w;
        g[v1][v2] = g[v2][v1] = w;  // 无向图
    }

    path.resize(n, INT_MAX);  // 初始化路径为无穷大
    b.resize(n, false);  // 初始化所有节点未访问
    temp.resize(n, INT_MAX);  // 初始化临时数组为无穷大
    num.resize(n, 0);  // 初始化路径数量
    res.resize(n, 0);  // 初始化救援队数量

    dijie(c1);

    cout << num[c2] << " " << res[c2] << endl;

    return 0;
}