据互联网数据统计2024年1-9月全国法拍房挂拍量为494737套,同比增长66.84%,挂牌金额超过5200亿!
法拍房暴增的背后是原业主的债务困境,或是房地产风险释放触底,或与规模高达10.61万亿的经营D相关。而对于不良资产行业机构来说,法拍房数量的增加,则会影响到金融机构D款抵押物的处置速度和价值变现。

挂牌量激增,折扣率骤减
在不良资产领域,法拍房属于极为常见的资产类别。法拍房主要是基于借款合同以及金融机构的申请,由法院强制执行进行拍卖的房屋,其形成原因主要有以下两点:其一,房D违约所致。当房产所有者不能持续支付房贷时,银行或贷款机构便会向法院申请强制执行拍卖房产,以此收回贷款。其二,抵押物拍卖引发。房产作为债务的抵押物,一旦债务人无法偿还债务,债权人能够申请法院对抵押的房产予以强制拍卖,进而清偿债务。
今年开年,法拍房数量就经历过一轮暴增,直到到第三季度,势头依旧不减。
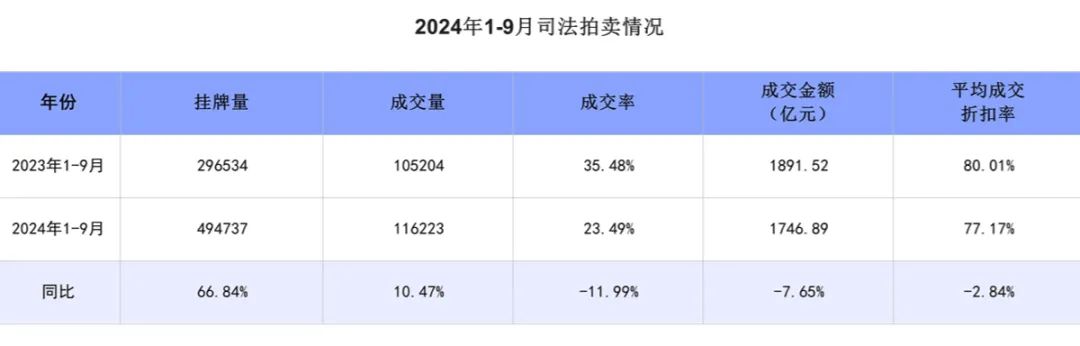
今年1-9月法拍房挂拍量为494737套;同比增长66.84%。
挂拍金额为5204.14亿元;成交量为116223套,成交率为23.49%;成交金额为1746.89亿;平均成交折扣率为77.17%,同比减少2.84个百分点。
在众多类型的法拍房中,住宅用房所占比例居于首位,为 48.47%。住宅用房和工业用房的成交率分别为 33.21% 和 30.85%,而商业用房的成交率相对偏低,仅为 17.68%。就折扣率方面而言,工业用房的成交价格在各类法拍房中是最高的一项。
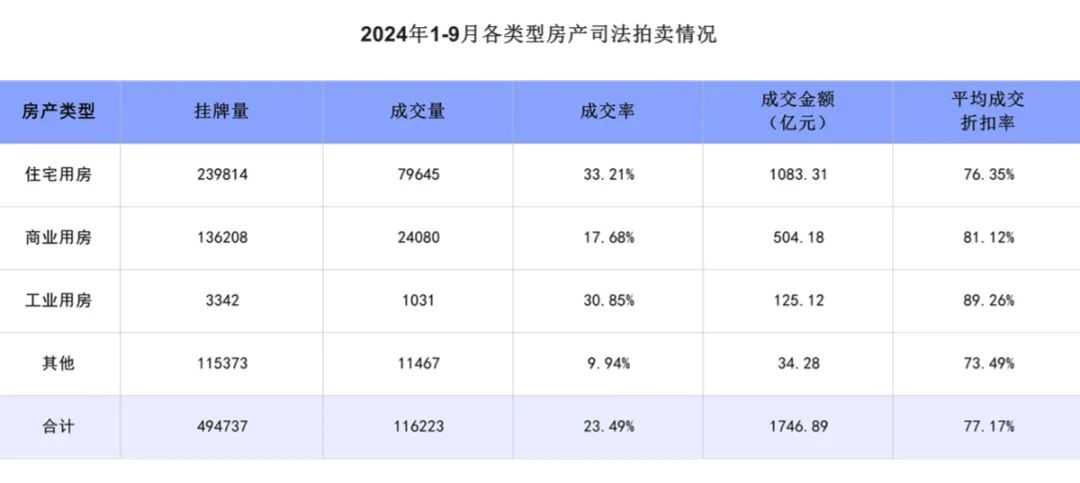
如果市场上法拍房数量占比达到20%,就会影响整个片区/城市的二手房价格。
2024 年 1 月至 9 月,在 10 个大中城市中,挂拍量处于较高水平的城市有成都、重庆、武汉、郑州和南宁,其挂拍数量分别为 24827 套、22886 套、10495 套、9859 套以及 7265 套;成交率较高的城市为杭州和温州,成交率各自达到 68.31% 和 63.31%;成交折扣率最高的城市是温州,折扣率为 94.29%;流拍率较高的城市分别是兰州和西宁,二者流拍率均超过 90%。
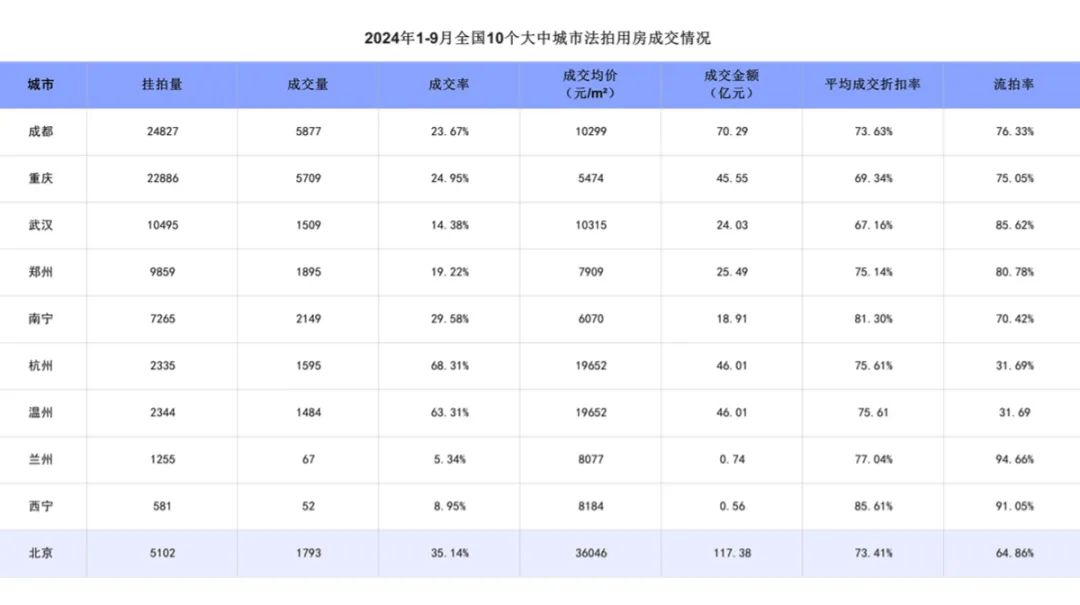
40个大中城市法拍房平均报名人数较多的城市分别是温州、杭州、上海、深圳、北京、苏州,平均报名人数破4。
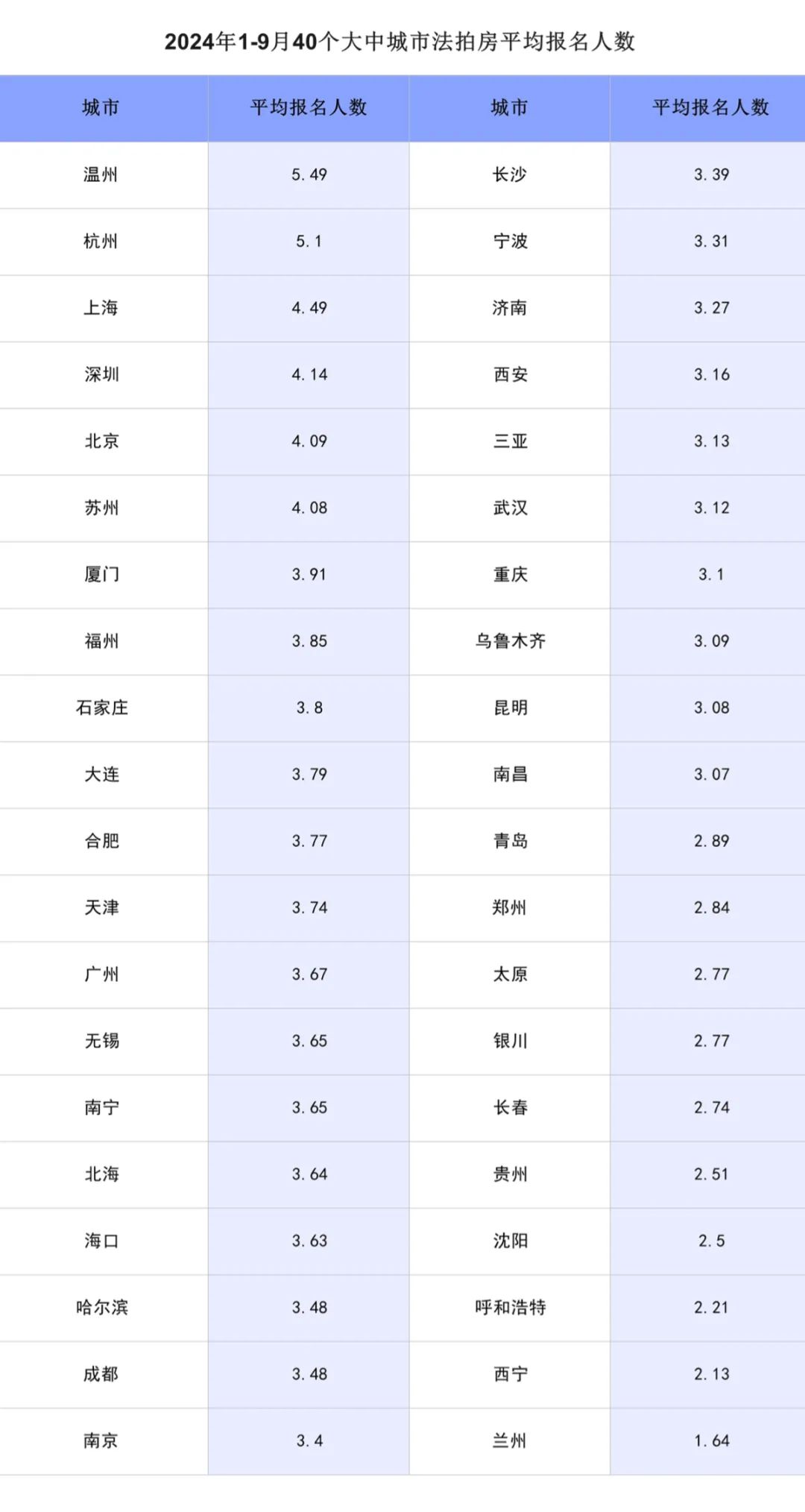

法拍房住宅用房情况
总体概况:
2024 年 1 月至 9 月,全国法拍住宅用房挂拍数量为 239814 套;成交数量为 79645 套,成交率达 33.21%;成交金额为 1083.31 亿元;平均成交折扣率是 76.35%。与 2023 年同期相比,全国住宅法拍房挂拍量同比增长 29.61%,成交量同比降低 1.05%,成交均价同比下降 13.23%,成交金额同比减少 10.12%,平均成交折扣率同比下降 3.69 个百分点。
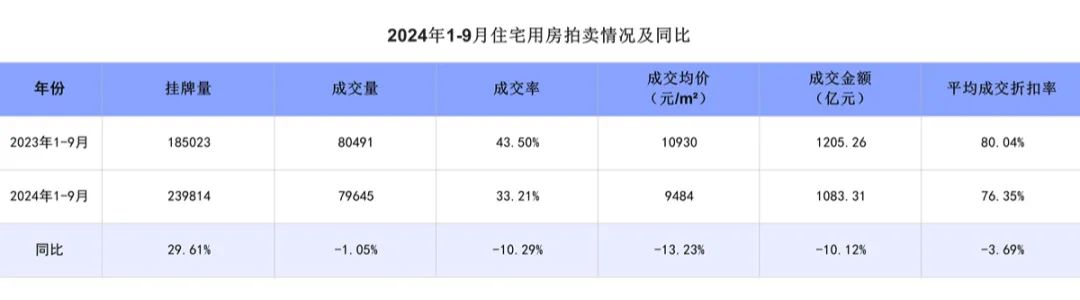
2.各城市概况:
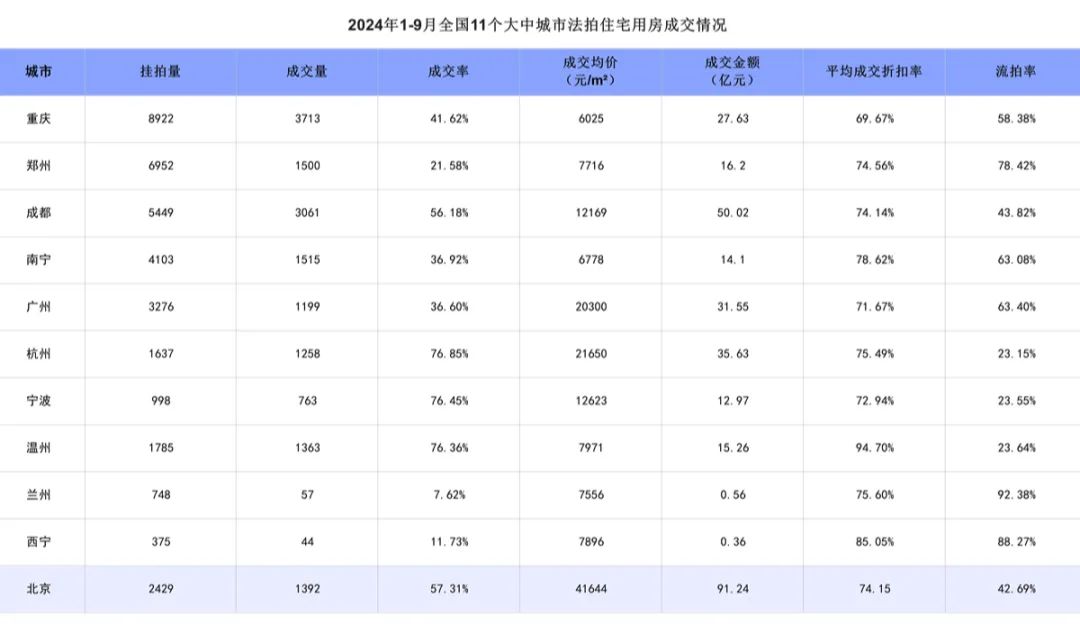
2024 年 1 月至 9 月期间,在全国已成交法拍住宅用房中,11 个大中城市里挂拍量处于较高水平的城市为重庆、郑州、成都、南宁和广州,其挂拍数量分别是 8922 套、6952 套、5449 套、4103 套以及 3276 套;成交率较高的城市有杭州、宁波和温州,成交率均超过 75%;成交折扣率最高的为温州;流拍率较高的城市分别是兰州和西宁,二者流拍率均高于 85%。
法拍房商业用房情况
总体概况
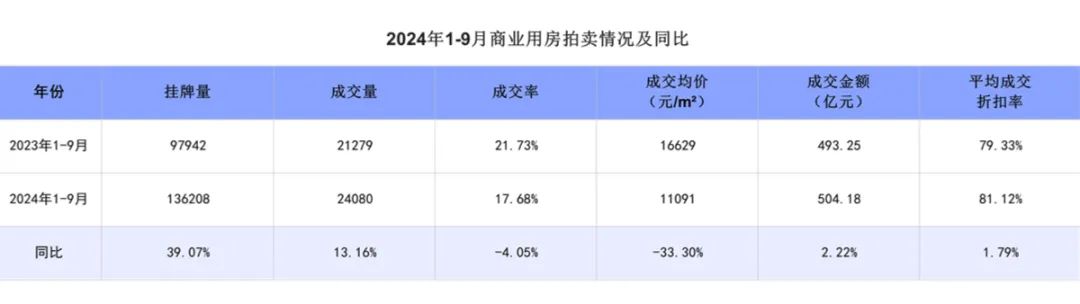
2024 年 1 月至 9 月,全国司法拍卖商业用房挂拍数量为 136208 套;成交数量为 24080 套,成交率为 17.68%;成交金额达 504.18 亿元;平均成交折扣率为 81.12%。与 2023 年同期相比,全国法拍商业用房挂拍量同比增长 39.07%,成交量同比增加 13.16%,成交均价同比下降 33.30%,成交金额同比上升 2.22%,平均成交折扣率增加 1.79 个百分点。
2.各城市概况:
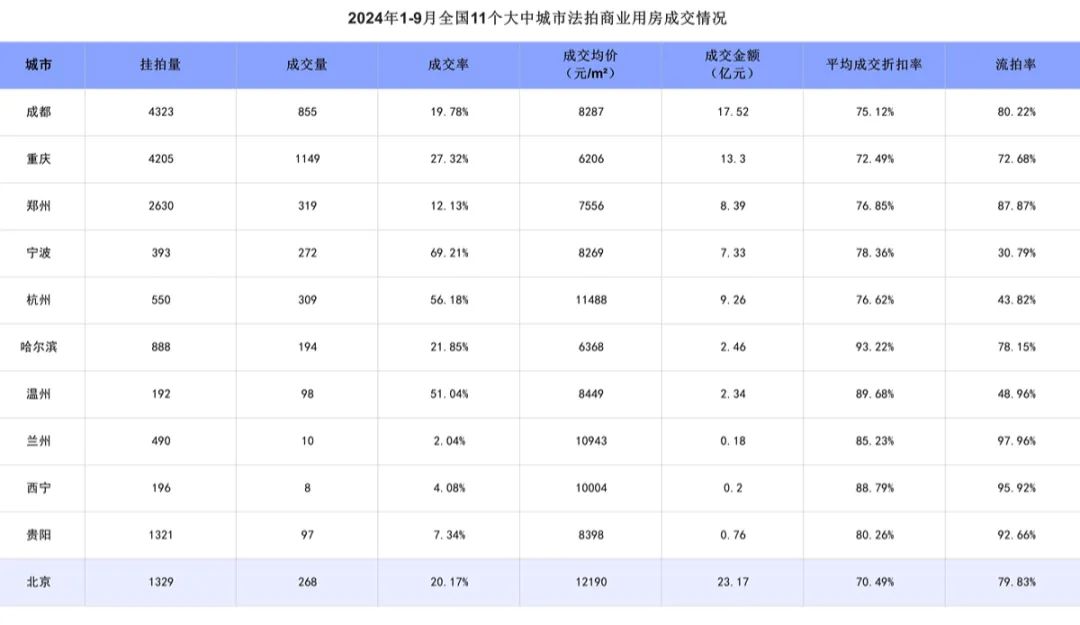
2024 年 1 月至 9 月,在全国已成交的法拍商业用房中,11个大中城市里挂拍量相对较高的城市为成都、重庆和郑州,其挂拍数量分别是 4323 套、4205 套和 2630 套;成交率较高的城市是宁波和杭州,二者成交率均超过 55%;成交折扣率处于较高水平的城市分别是哈尔滨和温州;流拍率较高的城市有兰州、西宁和贵阳。

如今,法拍房市场的火爆,的确为购房者提供了难得的购房机会,但!购买法拍房并非毫无风险。看似“便宜”的商业交易背后,很可能暗藏了“陷阱”。多次抵押、恶意租赁、非法侵占、户籍霸占……每一个问题,都能让你崩溃。便宜,是法拍房最大的诱惑,也是最大的陷阱。如果你不是专业人士,也不想寻求专业人士的帮助,那我给你的建议只有一个:
珍爱生命,远离法拍房。