PISA架构芯片资源排布研究
随着全球“芯”缺浪潮的持续发酵,作为“工业粮食”的芯片技术成为我国亟待突围的产业之一。PISA作为兼具良好处理速度与可编程性的交换芯片架构,有效缓解了传统固定功能的交换芯片研发效率低下的问题。为充分发挥芯片能力,高资源利用率的芯片资源排布算法的选择显得尤其重要。鉴于此,本文将复杂的基本块资源排布问题拆解为多个子问题,并结合各类约束条件,通过建立目标规划模型与基本块排布模型逐步求解,然后设计启发式规则对求解结果进行优化,最终将得到的尽可能短的流水线级数作为问题的解。
针对问题一,本文将其划分为依赖关系分析和基本块资源排布两个子问题。针对子问题一,分析处理附件 attachment3. csv数据得到控制流图CFG与控制流图的前向支配树FDT, CFG和FDT差集即为基本块的控制依赖关系。其次, 读取附件 attachment2. csv中基本块的读写关系,利用广度优先搜索算法BFS判断基本块间的连通性来确定数据依赖关系。将控制依赖与数据依赖关系取并集得到完整的依赖关系。针对子问题二,将完成的依赖关系抽象为带权有向无环图,初步确定基本块在流水线中排布的层级关系。然后,以占用尽量短的流水线级数为主要目标,结合 attachmentl. esv中的基本块资源需求和给定的资源约束条件建立了目标规划模型。模型的求解设计了基本块排布模型,依据串行排布的原则,从无前序依赖关系的基本块中依据随机规则选取基本块放入最早可放入的流水线级,直到所有基本块完成排布。
问题一得出流水线占用级数为40级。
针对问题二,由于不在一条执行流程上的基本块可以共享 HASH资源和ALU资源,我们在问题一的基础上引入不在一条执行流程上的基本块的概念,缓解了问题一中对HASH和ALU的占用问题。本文将问题二拆解为判断两个基本块是否在同一条执行流程、基本块资源排布两个子问题。针对子问题一,根据程序流程图,利用广度优先搜索算法判断两个基本块是否在一条执行流程上,即从一个基本块出发是否可到达另一个基本块,获得基本块执行流程关系对称矩阵。针对问题二,同样以占用尽量短的流水线级数为主要目标,结合不在同一执行流程上的基本块可共享HASH和ALU资源这一条件与更改后的三个约束,建立与问题一类似的目标规划模型。求解时对于有新的基本块排布的流水线,合并该级流水线中与其处于不同控制流的基本块对HASH和ALU的资源需求。
问题二得出流水线占用的级数为34级。
求解方案优化考虑到随机规则选取的不稳定性,对基本块选取规则进行优化,本文构建了最早开始时间EST、最多紧后资源块MST、最早开始时间且最多紧后资源块EST MST等6种启发式规则,依据启发式规则选取要加入流水线的基本块。本文综合了10次随机规则和6种启发式规则求解的最优结果作为最终的流水线排布方案。优化后,问题一得出流水线占用级数为40级。问题二得出流水线占用的级数为34级。
最后,本文发现了问题一的性能瓶颈在于HASH资源,问题二的性能瓶颈在于TCAM 资源。通过综合考虑控制依赖、数据依赖和各级流水线的资源约束条件,证明了所提方案的有效性与普适性。总结了所提算法与模型的优缺点,并对未来研究工作进行了展望。
关键词:PISA:资源利用率:基本块资源排布问题; 目标规划模型:随机算法; 启发式算法
问题重述
1.1 问题背景
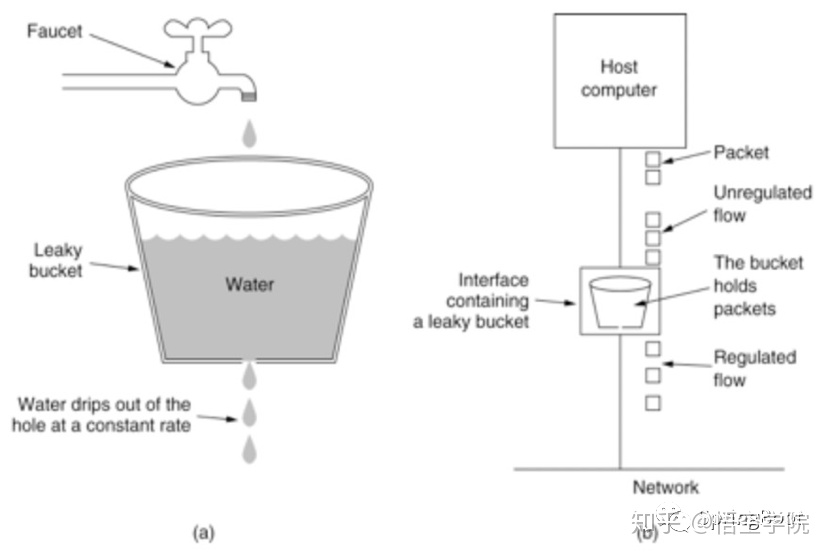
在全球“芯”缺浪潮持续发酵的形势下,作为“工业粮食”、安全根本的芯片是各个大国必争的高科技技术,是我国亟待突围的产业之一。传统固定功能的交换芯片,随网络协议的更新而需重新设计,这大大降低了研发效率,为此,诞生了可编程的交换芯片。兼具良好处理速度与可编程性的交换芯片架构PISA ( Protocol Independent Switch Architecture), 是当前主流之一。PISA 架构包括报文解析、多级的报文处理流水线与报文重组三个部分。本课题在只关注多级报文处理流水线部分的前提下,解决PISA架构芯片资源排布问题,即由P4语言得到的P4程序在经编译器编译时,首先会被划分为系列基本块,随后将各基本块排布到流水线各级当中。为充分发挥芯片能力,需考虑多种约条件束,找到高资源利用率的资源排布算法。
1.2 问题提出
题目给出 attachmentl. csv、 attachment2. csv、 attachment3. csv 三个附件, 分别表示了各基本块使用的资源信息、各基本块读写的变量信息、各基本块在流程图种的邻接基本块信息。充分挖掘各基本块间的数据依赖、控制依赖关系,建立相应的资源排布模型及算法,进一步解决以下问题:
问题一:结合给定的资源约束条件,实现资源排布并优化,使占用的流水线级数尽量短,以求最大化芯片资源利用率,要求输出基本块排布结果。
问题二:数据流图中,不在同一条执行流程上的基本块(从一个基本块出发不可达另一个基本块),可以共享HASH资源和ALU资源,即不在同一条执行流程上的基本块,任一个的HASH资源与ALU资源均不超过每级资源限制,就可排布到同一级。结合题目更改后的资源约束条件,实现资源排布并优化,使占用的流水线级数尽量短,并输出基本块排布结果。
2模型假设
[1]假设实验场景均位于理想状态,不受温度和电磁等因素影响。
[2]假设实验过程中不存在由芯片故障导致的误差。
[3]假设只关注 PISA 架构芯片多级的报文处理流水线部分。
[4]假设每级流水线除题目所给的资源约束外,其他条件均相同。
[5]假设可排布的流水线级数没有上限。
[6]假设随机模型种取随机数的过程是完全随机的
符号说明
本文中所用符号的说明如下表所示。
| 符号 | 说明 | 备注 |
| GW | 带权有向无环图 | |
| weight(u,v) | 表示(u,v)偏序关系 | 0:小于等于, 1:严格小 |
| B | 基本块集合 | 于 |
| duk | 基本块u对资源k的需求 | |
| P | 基本块分布矩阵 | N×N方阵 |
| pui | 基本块u放在第i级流水线 | |
| R | 流水线资源使用矩阵 | 4×N |
| rkj | 第j级流水线对资源k的使用 | |
| M | 流水线级数序号集合 | |
| Li | 基本块i可放入的最早流水线级数 | i=0... N |
| DINi | 基本块i的入度 | i=0…N |
| C | 矩阵(1,0,1,0,…)T | N×1 |
| qua | 有向无环图中有向边(u,v)的权值 | |
| E | 流程约束矩阵 | N×N方阵 |
| G | 基本块邻接关系图 | N×N方阵 |
| GF idomGF | 基本块邻接关系逆序图 基本块的前向支配图 | N×N方阵 N×N方阵 |
4问题一的模型建立与求解
4.1 问题分析
问题一要求考虑各基本块间的数据依赖、控制依赖关系情况下,结合给定的资源约束条件,实现基本块资源排布并优化,使占用的流水线级数尽量短,以求最大化芯片资源利用率。题目给出 attachment1. csv、attachment2. csv、attachment3. csv三个附件分别为各基本块使用的资源信息、各基本块读写的变量信息以及各基本块在流程图种的邻接基本块信息。
通过对题目分析,我们得出本题可拆解为以下三个子问题:
子问题一:通过设计算法与模型,对附件二、附件三中的数据进行处理分析,确定各基本块间的控制依赖关系与数据依赖关系,从而初步确定基本块在流水线中排布的层级关系。
子问题二:结合题目所给资源约束条件与附件一的资源使用数据,建立模型,确定基本块在流水线中的级数排布情况。
子问题三:对基本块排布进行优化,使得基本块占用的流水线级数尽可能短。
4.2模型建立与求解
4.2.1 依赖分析模型
为初步确定基本块在流水线中排布的层级关系,我们首先对附件二 attachment2. csv 与附件三attachment3. csv中的数据进行了预处理,分别得到具有数据依赖的基本块对集合与有控制依赖关系的基本块对集合。在此基础上,我们对两个集合进行合并,得到基本块偏序关系集合,即流水线级数关系分别为严格小于和小于等于的两个列表。模型建立流程如图4-1所示。

模型实现伪代码如表4-1所示。
表4-1
确定依赖关系伪代码
输入: attachmentl. esv, attachment2. csv, attachment3. csv
输出: dependence L, dependence LE
1: attachment3. csv→linkList #存取各基本块在程序流程图中的邻接关系
2: linkList→G, GF #将邻接关系及其逆序转化为图
3:GF+根节点→idomGF #获取邻接关系的前项支配图
4: for G中的每条边(i,j):
5: if(i,j)∉idomGF:
6: (i,j)→control dependance less equal #存入小于等于的控制依赖列表
7: end
8: attachment2.csv→wr dict #提取基本块与相关变量的读写关系
9: wr dict→ddg dict #将以基本块为键值的字典转化为以变量为键值的字典
10: for ddg dict中的每个变量:
11: if该变量对应的基本块对(i,j)之间存在通路:
12: if(i,j)存在写后写, 写后读关系:
13: (i,j)→data dependance less #存入严格小于的数据依赖列表
14: end
15: if(i,j)存在读后写关系:
16: (i,j)→data dependance less equal #存入小于等于的数据依赖列表
17: end
18: end
|
|
|
19: all less equal control dependance less equal data dependance less equal |
|
U |
20: all less equal→dependence LE
21: data dependance less→dependence L
(1) 控制依赖分析
控制依赖是程序控制流导致的一种约束。设A和B为某程序中的两个节点,若B能否执行取决于 A的执行结果,则称B控制依赖于A。通俗地讲,若节点B控制依赖于节点A,则要求A与B之间可达,A至少有两个直接后继节点。因此,若节点B是节点A 的唯一直接后继,则B并不控制依赖于A。PISA架构中,若基本块A与基本块B存在控制依赖,则A排布的流水线级数需要小于或等于B排布的流水线级数。
方法思想:附件三给出各基本块在流程图中的邻接基本块信息,我们需建立数学模型以分析各基本块间的控制依赖关系,从而得到它们在流水线中排布的级数关系。首先,
8
我们将附件三数据信息转换为控制流图CFG( Control Flow Graph)。其次, 反转控制流图CFG,并添加根结点,进一步求得反向控制流图的支配树,即为CFG 的前向支配树FDT( Forward dominance Tree)。最后,我们查找在CFG中, 但不在FDT中的边, 得到存在控制依赖关系的基本块集合S。
1)控制流图CFG
控制流图(程序流程图) 也即一个有向图,当程序被划分为基本块后,若将基本块视为一个基本单元节点,在程序执行流程上互为前驱和后继关系的两个基本块之间可视作存在一条有向边,整个程序就能转换为一个有向图G。
以表4-2数据集为例,我们可将其转化为如图4-2所示控制流图。
表4-2
| 基本块序号 | 邻接基本块序号 |
| 0 | 1 |
| 1 | 2, 3 |
| 2 | 4, 5 |
| 3 | 5, 7 |
| 4 | 6 |
| 5 | 6 |
| 6 | 7 |
| 7 8 | 8 |

2)前向支配树FDT
对于有向图G,设起点为s,终点为t,s->t之间可能存在多条路径,所有从s到t的路径中都必经的点,我们称之为支配点。删除该点,将不再存在由s可达t的路径,因此称起点为s时,该点支配了t。s->t中可能有许多支配点,由这些支配点构成的树,称为
(3) 依赖关系图模型
图论是研究点、线间关系的一门学科,属于应用数学的一部分。现实生活中,凡是涉及到事物间的关系,都可以抽象为图论模型。据于此,我们可以将上述求得的控制依赖关系与数据依赖关系映射到一个带权有向无环图中。
由于 4.2.1得到的控制依赖全部都是小于等于的偏序关系,可以将 data dependance less equal与 control dependance less equal取并集去除重复项。至此, 我们可以获取到由所有控制依赖和数据依赖条件提取出的两组流水线级数偏序关系列表,偏序关系为小于等于的基本块对列表 dependence LE 和偏序关系为小于的基本块对列表 dependence L。
我们用点表示基本块,连线表示基本块之间的读写关系,如果连线存在,表示两端的基本块对相同的变量有读写关系。为进一步区分读写关系的“读后写”“写后读”“写后写”,我们构造了带权的有向图,刻画事物间的联系(比如城市间的距离),就给连线赋一个权值,从而抽象成赋值图。
4.2.2基本块排布模型
(1) 模型建立
对流水线基本块分配问题进行需求分析,抽象问题并建立数学模型。建模过程需要考虑资源约束条件,优化目标等属性及基本块相互间的依赖关系,为更好的通过数学语言描述问题,我们建立如下变量:
R={k|k=0,1,2,3}:资源集合, 其中0:TCAM,1:HASH,3:ALU,4:QUALIFY
B={u|u=0,……,N},N=606:基本块集合
M={i|i=0,…,N}:流水线级数序号集合
L₁:基本块i所在流水线级数列表
duk: 基本块u对资源k的需求
Pui: 基本块u放在第i级流水线
rki: 第i级流水线对资源k的使用
|
|
|
该级有基本块 |
|
该级无基本块 |
qu,v: 有向无环图中有向边(u,v)的权值
|
quv=1,0, |
|
基本块u 流水线级数小于等于基本块v |
结合题目描述,目标函数可表述为在满足基本块依赖关系与流水线各级资源限制的情况下,尽量减少流水线的级数,可以抽象为:
min∑i=0Nmi![]() (1)
(1)
根据题目要求,还需以下约束条件:
1)依赖关系约束
基本块排布时需考虑它们之间的控制依赖与数据依赖关系,从而确定它们所在的流水线层级关系。若有向无环图GW中有向边权值为1,则两个基本块在流水线中排布的级数为严格小于关系,若有向边权值为0,则两个基本块在流水线中排布的级数为小于等于关系,由此可以抽象为:
Lᵤ<Lᵥ,qᵤᵥ=1![]() (2)
(2)
|
2)资源约束 |
|
Lᵤ≤Lᵥ,qᵥₓ=0 |
设i级流水线包含的基本块集为M(i),则第i级流水线对第k种资源的需求量为:
rₖₗ=∑dₖ,vi∈Mi![]()
由题目给出条件建立约束:
r0λ≤1![]() (4)
(4)
r1,i≤2![]() (5)
(5)
r₂₁≤5![]() (6)
(6)
r3λ≤64![]() (7)
(7)
3)折叠约束
题目规定流水线第0级与第16级,第1级与第17级,...,第15级与第31级为折叠级数,折叠的两级TCAM资源加起来最大为1,HASH 资源加起来最大为3。若所需的流水线级数超过32级,则从第32开始的级数不考虑折叠资源限制。据此,可抽象为:
r0,i+r0i+16≤1,i0.15![]() (8)
(8)
r1,i+r1,i+16≤3,i0.15![]() (9)
(9)
4)TCAM偶数级约束
设矩阵C=(1,0,1,0…)F,则约束“有TCAM资源的偶数级数量不超过5”可以抽象为:
∑i=0ℏr0,2*C≤5![]() (10)
(10)
5)基本块只能排到一级流水线约束
题目要求每个基本块只能排到一级流水线约束,可以抽象为:
vi,∑i=0Npu=1![]() (11)
(11)
综上所述,我们可以得到问题一的目标函数模型,如下所示:
min∑i=0Nmi![]() (1)
(1)
(2) 模型求解与优化
通过建立依赖关系模型,对附件 attachment2. csv与attachment3. csv中数据预处理后,得到基本块在流水线中排布的初步依赖关系,流水线排布过程中对所有基本块进行如下规定:
·前序基本块:两个基本块的依赖关系中需要优先排布的块:
·后序基本块:两个基本块的依赖关系中需要靠后排布的块:
·FB:完成流水线排布的基本块集合:
·CB:所有前序基本块都处于FB的基本块集合;
·NB:未完成流水线排布的基本块集合。
依据串行进度生成机制,优先排布前序基本块全部放入流水线的基本块,即集合CB 中的基本块。CB是一系列无前序依赖关系的基本块集合,不断从中随机选取一个基本块,计算其最早可排入的流水线级数,并将其排布该级流水线,并更新依赖关系CB与基本块集合CB和NB。NB为空说明所有基本块都已排入流水线。流水线排布算法的伪代码如表4-4所示。
表4-4
| 流水线排布算法 | |
| 输入: attachmentl. csv, dependence _L, dependence _LE, Resources | |
| 输出: L, P | |
| 1 dependence _L, dependence _LE→GW, DIN, CB, neignbors, neighbors _ len | |
| #根据依赖关系建立有向带权图GW和初始状态下模型参数 | |
| 2 | attachment1. csv→D #基本块所需的资源 |
| 3 | while GW 中的基本块数量>0: |
| 4 | for CB 中的每个基本块u: |
| 5 | while(1): |
| 6 7 | if把基本块u放入流水线L₀级别满足资源约束: |
| break | |
| 8 | else: |
| 9 | Lu++#更新基本块u的最早可放入级数 |
| 10 | end |
| 11 | CB→u#从CB 中随机选取基本块u |
| 12 | level= L₀#放入流水线L₀级 |
| 13 | Pujevel=1 |
| 14 | R=D*P |
| 15 | for基本块u的所有后序基本块v: |
| 16 17 | Lv= Lu+ weight(u,v) |
| DIN、-- | |
| 18 | CB-{u}+{v|v 的入度为0} |
| 19 20 | 删除GW的边(u,v) 删除GW的删除基本块u |
算法的具体实现如下:
步骤1:根据依赖关系建立有向带权图GW并获取模型所需参数。
1)初始化有向带权图GW,GW包含所有未完成流水线排布的基本块。
①将全部基本块B作为GW的结点GW. nodes:
GW. nodes = {u|u∈B}
②将基本块的依赖关系作为GW的边GW. nodes;
GW. edges={(u,v)|∀(u,v)∈dependence L}
GW. edges={(u,v)|∀(u,v)∈dependence LE}
③根据依赖关系的不同为GW的边添加权重,对于基本块u,v的依赖关系(u,v),如果依赖关系要求基本块u,v在流水线排布级数为严格小于关系,就将GW的边(u,v)的权重设置为1:如果依赖关系要求基本块u,v在流水线排布级数小于等于,就将GW的边(u,v)的权重设置为0;
weight(w.)={0,(u,v)e dependence LE
GW. edge(u,v). weight= weight(u,v),∀(u,v)∈dependence L∪dependence LE
2)初始化基本块入度DIN和CB
①统计GW中所有结点的入度:
DIN.. =|{u|(v,u)∈GW. edges(),v∈B}|,u∈B
②将入度数为0的点存入CB中,表示该点在流水线排布时间可被选择:
CB ={u|u∈B. 且 DlNᵤ-O;![]()
3)统计所有的后继结点以及后继结点的数量供后续使用:
neighborsu=|{v|(v,u)∈GW. edges(),v∈B}|
neighbors len..= |neighborsu|
4)初始化资源需求矩阵D,流水线排布矩阵P,最早可排入流水线L,4中流水线资源表 Resources
①从 attachmentl. csv文件中读取基本块对4种资源的需求:
DK,u= 基本块u对资源k的需求,k∈{0,1,2,3},u∈B
②初始状态下流水线中没有基本块:
Puj=0,u∈B,i∈{0,1,2,…,N}
③初始状态下未考虑任何依赖关系,所有块的最早均可第0级排入流水线:
Lᵤ=0,u∈B![]()
④TCAM、HASH、ALU、QUALIFY这4种资源的数量:
Resources={1,2,56,64}
步骤2:更新GW中所有基本块最早可放入流水线的级数。
对于基本块u,尝试将其放入流水线 Lu级,如果放入后满足资源资源约束
代码
| import networkx as nx import matplotlib. pyplot as plt import numpy as np import csv import sci py as sp #入度 inGF=□ #第一步: dfs dfn=[] rak=[] fa=[] search _ path=[] #第二步: sdom val=[] bel=[] sdom=[] #第三步: idom idom=[] #比较获取 CDG cdg=[] idomGF= nx. DiGraph() def read _csv3( file _ name): f= open( file _ name, encoding='UTF8') csv _ reader= csv. reader(f) control _ edges=[] for line in esv _ reader: adj _ num= len( line) if adj _ num>1: for i in range(1, adj _ num): control _ edges. append(( int( line[0]), int( line[i]))) f. close() # print( control _ edges) return control _ edges def subgraph(pointList, linkList): G= nx. DiGraph() GF= nx. DiGraph() #转化为图结构 for node in pointList: G. add _ node( node) |
| GF. add _ node( node) for link in linkList: G. add _ edge( link[0], link[1]) GF. add _ edge( link[1], link[0]) return G, GF def dfs(GF): #GF的 root为人为添加的序号最大的根 root= len(GF. nodes)-1 T= nx. dfs _ tree(GF, root) for n in GF. nodes(): fa. append(0) dfn. append(n) global rak rak= list(T) #所有节点 for i in range(0, len( fa)): dfn[ rak[i]]=i for i in list(T. edges): #所有边 fa[i[1]]=i[0] # print( dfn) # print( rak) # print( fa) def find(v): #还未被遍历 ifv== bel[v]: return v tmp= find( bel[v]) if( dfn[ sdom[ val[ bel[v]]]]< dfn[ sdom[ val[v]]]): val[v]= val[ bel[v]] bel[v]= tmp return bel[v] def tarjanFDT(): #初始化 val和 sdom for i in range(0, len( dfn)): val. append(i) sdom. append(i) bel. append(i) idom. append(i) #从大到小遍历 dfs树 for i in range( len( dfn)-1,0,-1): # dfs序最大的点u u= rak[i] #获取GF原图中所有u的前驱 neighbors=G. neighbors(u) |
for v in neighbors:
find(v)
if( dfn[ sdom[ val[v]]]< dfn[ sdom[u]]):
sdom[u]= sdom[ val[v]]
# print( sdom)
sdomGF= nx. DiGraph()
forii n range(0, len( sdom)):
sdomGF. add node(i)
sdomGF. add edge( sdom[i], i)
bel[u]= fa[u]
u= fa[u]
neighbors=sdomGF. neighbors(u)
for v in neighbors:
find(v)
if sdom[ val[v]]==u:
idom[v]=u
else:
idom[v]= val[v]
for i in range(0, len( dfn)):
u= rak[i]
if idom[u]!= sdom[u]:
idom[u]= idom[ idom[u]]
global idomGF
for i in range(0, len( idom)):
idomGF. add node(i)
idomGF. add edge( idom[i],i)
# nx. draw networkx(sdomGF, with labels= True)
# plt. show()
# nx. draw networkx(idomGF, with labels= True)
# plt. show()
def getInGF():
#遍历 GF所有点
for i in range(0, len(GF. nodes)):
#初始化:0标识入度为0
inGF. append(0)
for edge in GF. edges:
inGF[ edge[1]]=1
def addGFRoot():
# print( len(GF. nodes))
GF. add node( len(GF. nodes))
forii n range(0, len(inGF)):
if inGF[i]==0:
GF. add edge( len(GF. nodes)-1,i)
# nx. draw networkx(GF, with labels= True)
# plt. show()
if name ==' main ':
#读 attachment3. evs
linkList= read csv3("./ data/attachment3. csv")
pointList=[]
for i in range(0,607):
pointList. append(i)
#原始有向无环图G,反向图GF
G, GF = subgraph(pointList, linkList)
#获取GF 入度为0的所有点
getInGF()
#为GF添加根节点
addGFRoot()
#获取G的前向支配树,也就是GF的支配树,存储在 idomGF中(即FDT)
dfs(GF)
tarjanFDT()
#对比G原图和FDT图,寻找在G但不在FDT中的边,得到CDG
for edgeG in G. edges:
edgeGf=(edgeG[1], edgeG[0])
#标识是都存在相同,初始化为0
flag=0
for edgefdt in idomGF. edges:
if edgeGf== edgefdt:
flag=1
break
else:
continue
if flag--0:
cdg. append(edgeG)
f= open("./ data/ control dependance less equal. txt", "w")
f. writelines( str( cdg))
f. close()
print( len( cdg))
print( cdg)