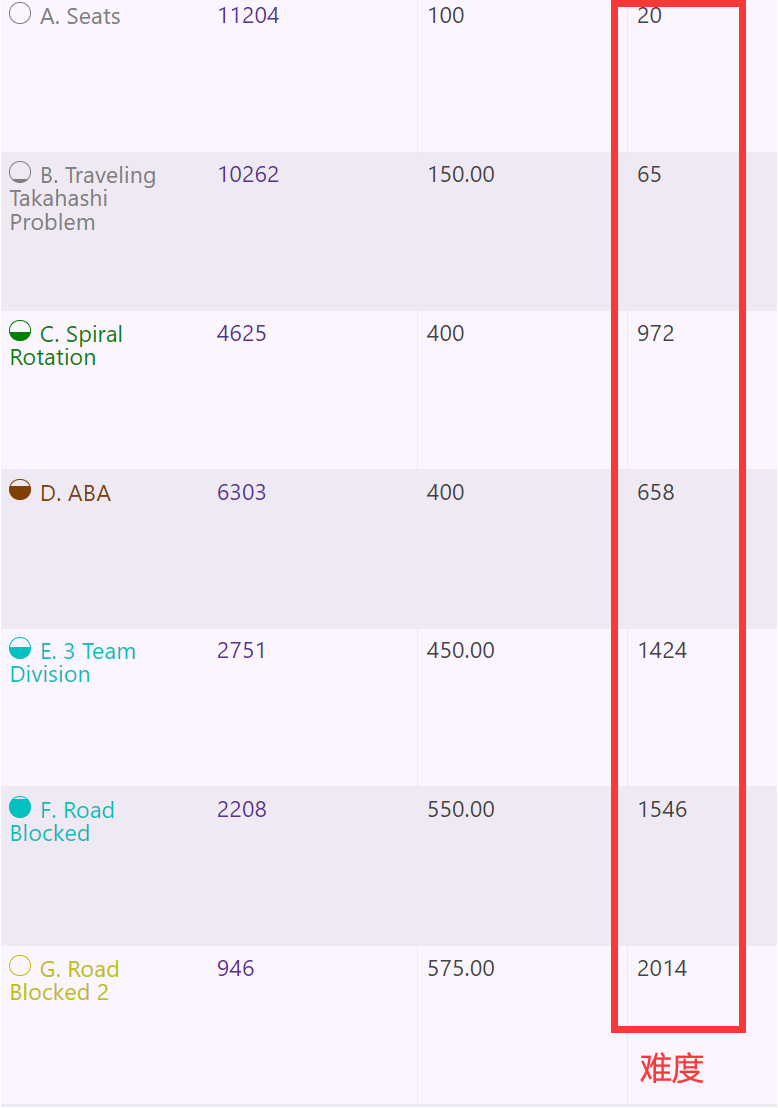
【模板】最长公共子序列
题目描述
给出 1 , 2 , … , n 1,2,\ldots,n 1,2,…,n 的两个排列 P 1 P_1 P1 和 P 2 P_2 P2 ,求它们的最长公共子序列。
输入格式
第一行是一个数 n n n。
接下来两行,每行为 n n n 个数,为自然数 1 , 2 , … , n 1,2,\ldots,n 1,2,…,n 的一个排列。
输出格式
一个数,即最长公共子序列的长度。
样例 #1
样例输入 #1
5
3 2 1 4 5
1 2 3 4 5
样例输出 #1
3
提示
- 对于 50 % 50\% 50% 的数据, n ≤ 1 0 3 n \le 10^3 n≤103;
- 对于 100 % 100\% 100% 的数据, n ≤ 1 0 5 n \le 10^5 n≤105。
题解
普通的LCS解(会TLE or MLE)
这题最开始我想着模版LCS,所以就默写了一个 真模版 LCS上去,(模版LCS问题这里就不讲了,个人觉得是一种数字三角形的变形题目)
def Solution1():
N = int(input())
Nums1 = [0] + list(map(int, input().strip().split()))
Nums2 = [0] + list(map(int, input().strip().split()))
dp = [[0 for _ in range(N+1)] for _ in range(N+1)]
for i in range(1, N+1):
for j in range(1, N+1):
dp[i][j] = max(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]+1 if Nums1[i] == Nums2[j] else 0)
print(dp[N][N])
Solution1()

我擦,懵了,这特么什么情况,不是模版题吗???
转换成LIS问题
我去查看了几篇题解,这才明白这道题的情况
首先我们看看LIS问题:
举例:
4 5 3 1 6 7 2
求上面这个序列的最长上升子序列
怎么求?
正常的想法就是用最长上升子序列的方法求,贪心解
(
O
(
n
l
o
g
n
)
)
(O(nlogn))
(O(nlogn)),或者dp解
(
O
(
n
2
)
)
(O(n^2))
(O(n2)),学过这方面的一般都是懂的,
但是求最长上升子序列问题还有一种思路
求最长上升子序列其实是求最长公共子序列
可能看到这有点懵了
继续举例:
4 5 3 1 6 7 2
1 2 3 4 5 6 7
求上面两个序列的最长公共子序列
我们发现,第一个序列的所有上升子序列,也一定是第二个序列的子序列,因为第二个序列就是1到7的单调排列。故而求最长的上升子序列,也是求最长的公共子序列。也就是说LIS问题可以转换成LCS问题。同理,这种情况的LCS问题也可以转换成LIS问题来解决。那么和这题有什么关系呢?
这题给了这样的一个神奇的限制条件:
接下来两行,每行为 n n n 个数,为自然数 1 , 2 , … , n 1,2,\ldots,n 1,2,…,n 的一个排列。
所以两个序列的数字总数一样为n, 而且是1到n的一种排列
举例:
3 2 1 4 5
5 4 3 2 1
我们假设有这样的一种大于小于情况:5<4<3<2<1
欸,那么上面的最长上升子序列就是3 2 1了!!
看明白了吗?
当我们把Nums2中下标小的数字看成小的数,下标大的数字看成大的数,那么Nums2就成了一种单调递增序列,而且是全排列的
所以就把刚刚上面那种情况复原出来了,也就是说LCS问题可以转换成LIS问题来解决。
下面给出关于这题的LIS贪心解(LIS的dp解不行)
def Solution2():
N = int(input())
Nums1 = list(map(int, input().strip().split()))
Nums2 = list(map(int, input().strip().split()))
# 将Nums2转换成 1 2 ... 13 14 ... 100 101的单调上升序列
idx = [0 for _ in range(N+1)]
for i in range(N):
idx[Nums2[i]] = i + 1
# 在Nums2中,形式上下标大的数比下标小的数大
# 转换成求Nums1的最长上升子序列问题
f = []
LenF = 0
for i in range(N):
left, right = 0, LenF
# 左闭右开
while left < right:
mid = left + right >> 1
# 如果 形式上 f[mid] < Nums1[i] (在idx上表示就是 idx[f[mid]] < idx[Nums1[i]])
# 去f的右边找更大的数,直至 形式上 Nums1[i] <= f[mid]
if idx[f[mid]] < idx[Nums1[i]]:
left = mid + 1
else:
right = mid
if len(f) <= right:
f.append(Nums1[i])
LenF += 1
else:
f[right] = Nums1[i]
print(LenF)
Solution2()