我的老师让我先做最后再交,看正确率(即以OI赛制打abc)
所以我用的小号(… …)
C 卡了老半天才出来,我把题读错了

难度:
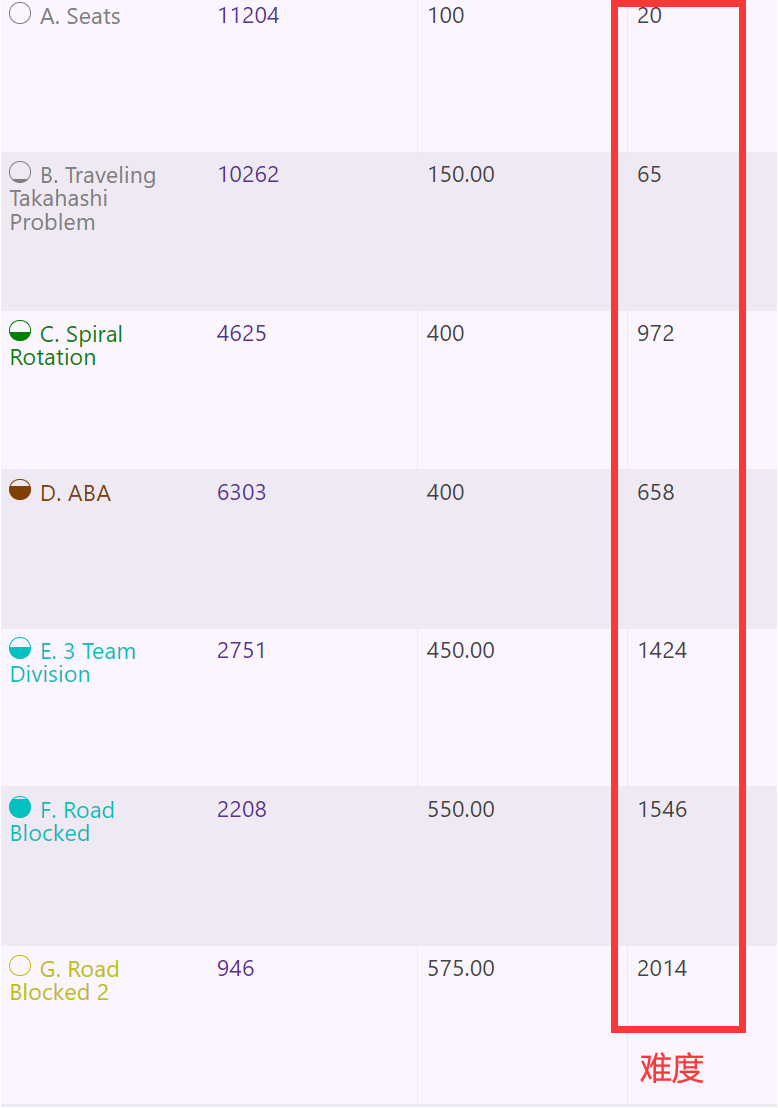
A. Seats
题意
给你一个字符串
S
S
S,仅包含 . 和 #,找出子串 #.# 的个数
思路
若下标从 0 0 0 开始,直接枚举 i ∈ [ 0 , n − 3 ] i\in [0,n-3] i∈[0,n−3] 即可
C++ 代码
#include<bits/stdc++.h>
using namespace std;
int n;
string s;
int ans;
int main(){
cin>>n>>s;
for(int i=0;i<n-2;i++){
if(s[i]=='#'&&s[i+1]=='.'&&s[i+2]=='#'){
ans++;
}
}
cout<<ans<<endl;
return 0;
}
B. Traveling Takahashi Problem
题意
给你平面上的 n n n 个点,第 i i i 个点坐标为 ( x i , y i ) (x_i,y_i) (xi,yi),现在需要从原点 ( 0 , 0 ) (0,0) (0,0) 出发,按顺序经过每个点,并回到原点 ( 0 , 0 ) (0,0) (0,0),问最终走过的距离。
注:从 ( x i , y i ) (x_i,y_i) (xi,yi) 到 ( x j , y j ) (x_j,y_j) (xj,yj) 的距离是 ( x j − x i ) 2 + ( y j − y i ) 2 \sqrt{(x_j-x_i)^2+(y_j-y_i)^2} (xj−xi)2+(yj−yi)2
思路
记录上次停留的位置,按顺序模拟即可
C++ 代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
long double ans;
int n;
int sqr(int x){
return x*x;
}
signed main(){
cin>>n;
int curx=0,cury=0;
for(int i=1;i<=n;i++){
int a,b;
cin>>a>>b;
ans+=sqrt(sqr(a-curx)+sqr(b-cury));
curx=a,cury=b;
}
ans+=sqrt(sqr(curx)+sqr(cury));
cout<<fixed<<setprecision(20)<<ans<<endl;
return 0;
}
C. Spiral Rotation
题意
有一个
n
∗
n
n*n
n∗n 的网格(
n
n
n 为偶数),设
(
i
,
j
)
(i,j)
(i,j) 为从上往下数第
i
i
i 行,从左往右数第
j
j
j 列的格子,每格要么是 . 要么是 #
对于 i ∈ { 1 , 2 , . . . , n / 2 } i \in \{ 1,2,\ ..., \ n/2\} i∈{1,2, ..., n/2}:
- 选择数对 ( x , y ) (x,y) (x,y) ,其中 1 ≤ x , y ≤ n + 1 − i 1\le x,y \le n+1-i 1≤x,y≤n+1−i,将 ( y , n + 1 − x ) (y,n+1-x) (y,n+1−x) 的值换为 ( x , y ) (x,y) (x,y)
- 对于所有符合要求的 ( x , y ) (x,y) (x,y),同时 进行以上操作
思路
由 $(y,n+1-x) $ = ( x , y ) (x,y) (x,y) 可得: ( i , j ) (i,j) (i,j) = ( n + 1 − j , i ) (n+1-j,i) (n+1−j,i)
那么共有以下四种情况:
-
( i , j ) = ( n + 1 − j , i ) (i,j) = (n+1-j,i) (i,j)=(n+1−j,i)
-
( n + 1 − j , i ) = ( n + 1 − i , n + 1 − j ) (n+1-j,i)=(n+1-i,n+1-j) (n+1−j,i)=(n+1−i,n+1−j)
-
( n + 1 − i , n + 1 − j ) = ( j , n + 1 − i ) (n+1-i,n+1-j)=(j,n+1-i) (n+1−i,n+1−j)=(j,n+1−i)
-
( j , n + 1 − i ) = ( i , j ) (j,n+1-i)=(i,j) (j,n+1−i)=(i,j)
-
下一次就又回到了第一种
所以只要看每一个操作了多少次 $\bmod 4 $ 的余数就可以了
C++ 代码
#include<bits/stdc++.h>
using namespace std;
string s[maxn];
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>s[i];
s[i]=" "+s[i];
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
int curi=(i>k?n-i+1:i);
int curj=(j>k?n-j+1:j);
int cur=min(curi,curj)%4;
if(cur%4==0){
cout<<s[i][j];
}else if(cur%4==1){
cout<<s[n+1-j][i];
}else if(cur%4==2){
cout<<s[n+1-i][n+1-j];
}else{
cout<<s[j][n+1-i];
}
}
cout<<endl;
}
return 0;
}
D. ABA
题意
给你一个字符串 s s s,你要选出三个下标: 1 ≤ i < j < k ≤ ∣ s ∣ 1\le i<j<k\le |s| 1≤i<j<k≤∣s∣,将 s i , s j , s k s_i, s_j,s_k si,sj,sk 拼接,使得拼接起来的字符串是 回文串
思路
对于 26 26 26 个字母,分别记录每种出现在哪些位置,再统一加减
C++ 代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
vector<int> g[26];
string s;
signed main(){
int n=sz(s);
s=" "+s;
for(int i=1;i<=n;i++){
g[s[i]-'A'].push_back(i);
}
int ans=0;
for(int i=0;i<26;i++){
if(g[i].size()==0) continue;
int sum=g[i][0];
for(int j=1;j<g[i].size();j++){
ans+=(j*g[i][j]-sum-j);
sum+=g[i][j];
}
}
cout<<ans<<endl;
return 0;
}
E. 3 Team Division
题意
共有 n n n 个人,已经分成了 3 3 3 组,第 i i i 个人在 a i a_i ai 组 ( 1 ≤ a i ≤ 3 ) (1 \le a_i \le 3) (1≤ai≤3),权值为 b i b_i bi,你可以重新分组,使得每组的 权值和 相等,且 换组的人数 最少
问最少换组的人数
思路
首先可以想到 d p [ i ] [ j ] [ k ] [ l ] dp[i][j][k][l] dp[i][j][k][l] 表示:前 i i i 个里面,第一组权值和为 j j j,第二组权值和为 k k k ,第三组权值和为 l l l
那么如何优化?去掉最后一维
因为前 i i i 个人权值和一定,所以直接用总和减去 j + k j+k j+k 就得到了 l l l
C++ 代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int inf=2e15;
const int maxn=105;
const int maxk=1505;
int n;
int pos[maxn],v[maxn];
int dp[maxn][maxk][maxk];
int sum[maxn];
signed main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>pos[i]>>v[i];
sum[i]=sum[i-1]+v[i]; //计算前缀和
}
if(sum[n]%3!=0){//特判:只有和为3的倍数才能分成3组
cout<<-1<<endl;
return;
}
for(int i=0;i<=n;i++){//初始化dp数组
for(int j=0;j<=sum[i];j++){
for(int k=0;k<=sum[i]-j;k++){
dp[i][j][k]=inf;
}
}
}
dp[0][0][0]=0;
for(int i=1;i<=n;i++){
for(int j=0;j<=sum[i];j++){
for(int k=0;k<=sum[i]-j;k++){
if(j>=v[i]){
dp[i][j][k]=min(dp[i-1][j-v[i]][k]+(pos[i]!=1),dp[i][j][k]);
}
if(k>=v[i]){
dp[i][j][k]=min(dp[i-1][j][k-v[i]]+(pos[i]!=2),dp[i][j][k]);
}
if(sum[i]-j-k>=v[i]){
dp[i][j][k]=min(dp[i-1][j][k]+(pos[i]!=3),dp[i][j][k]);
}
}
}
}
int ans=dp[n][sum[n]/3][sum[n]/3];
if(ans==inf){
cout<<-1<<endl;
}else{
cout<<ans<<endl;
}
return 0;
}