由于量子不确定性和量子态的测量过程而引入的随机波动,量子噪声不可避免。
经典噪声
想象一下,一个比特存储在硬盘驱动器上, 它与普通计算机相连,该比特从状态0或1开始,经过长时间,散乱的磁场很可能会导致比特被干扰,使其翻转。

图1 长时间存储后,硬盘中的一个比特有可能会以概率p翻转
可以用一个方程简洁地描述硬盘中单比特的行为。假设p0和p1是比特分别处于状态0和1的初始概率。令q0和q1为噪声发生后相应的概率。设X为该比特的初始状态,Y为该比特的最终状态,于是总概率为:
(1)
其中条件概率称为转换概率。我们把它写出来有
(2)
经典系统中一个稍复杂的噪声例子。想象一下,我们正在尝试构建一个经典电路来执行一些计算任务。不幸的是,一些用来构建电路的组件是有缺陷的。我们的电路包含一个输入比特X,紧接着对它施加两个(有故障的)非门,产生中间比特Y和最终的比特Z。假设第二个门与第一个门是否正常工作是相互独立的,这看起来是合理的。这种假设--连续噪声过程各自独立地产生作用--在许多情况下在物理上是合理的。它会引发一种被称为马尔可夫过程的特殊类型的随机过程X→Y→Z。物理上,马尔可夫性这种假设对应于引起第一个非门中的噪声环境独立于引起第二个非门中的噪声环境,一种可能的情形是,逻辑门在空间中相隔很远的距离。
总之,经典系统中的量子噪声可以用随机过程理论来解释。通常马尔可夫过程也是一个很好的假设。对于单阶段过程,输出概率通过等式与输入概率
相联系。
(3)
其中E是转移概率的矩阵,我们把它称为演化矩阵。因此,系统的末态与初态线性地联系起来。这种线性特性在量子噪声中也有,其中用密度矩阵代替了概率分布。
演化矩阵E必须具备哪些属性呢?要求如果是有效的概率分布,那么也必须是有效的概率分布。满足这个条件结果等价于对E的两个条件。首先,E的所有条目必须是非负的。这被称为正定性要求。否则就有可能在
中出现负概率。其次,E的所有列必须总和为1,这被称为完备性要求。假设这不成立。想象一下,假如第一列之和不为1。让
在第一个条目为1,而在其他地方都为零,我们看到
在此情况下不是有效的概率分布。
总而言之,经典噪声的关键特征如下:输入和输出概率之间存在线性关系,由所有项非负(正定性)且列总和为一(完备性)的转移矩阵来描述。涉及多个阶段的经典噪声过程由马尔可夫过程描述,前提是噪声由独立的环境引起。这些关键特征中的每一个在量子噪声理论中都有重要的类似物。
量子操作
基本的量子操作包括酉运算与测量。 量子操作中的酉演化和测量是量子力学中描述量子系统动态和状态变化的两大核心过程
带有物理动机的公理 算子和表示
与环境耦合的系统
1. 量子操作的酉演化(Unitary Evolution)
量子系统的酉演化描述了量子系统在闭合系统中的时间演化。它遵循薛定谔方程,保持系统的量子态规范化,并且是可逆的。
1.1 酉算符(Unitary Operator)
一个酉算符 UUU 是一个满足以下条件的算符:
(4)
1.2 酉演化的特点
量子系统的时间演化由酉算符描述。给定量子系统的初态为
(5)
其中,是描述系统从初始时刻到时间t的酉演化算符。
酉演化具有以下特定:

1.3 薛定谔方程
量子系统的时间演化由薛定谔方程描述:
(6)
其中,H是系统的哈密顿量,描述系统的能量以及外界的相互作用。 该方程的解为:
(7)
这里的演化算符是一个酉算符,确保量子态的归一化。
2. 量子操作的测量(Quantum Measurement)
量子测量是量子力学中的另一个核心概念,它描述了对量子系统进行观测时,系统的状态发生坍缩的过程。量子测量是不可逆的,并且通常是伴随随机性发生的。
2.1 测量算符(Measurement Operator)
在量子力学中,测量与一个可观测量 O 相关联。可观测量 O 是一个自伴算符,其本征值表示测量可能得到的结果,其本征态代表系统可能坍缩到的状态。可观测量 O 的本征态 ∣ϕi〉 和本征值 λi 满足:
(8)
2.3 投影测量(Projective Measurement)
投影测量是最常见的一种量子测量。测量过程可以用一组正交投影算符 {Pi}表示,它们满足:
,
(9)
测量到结果为i的概率是:
(10)
测量后系统坍塌到投影算符作用下的状态:
(11)

3. 酉演化与测量的区别与联系
- 酉演化是量子系统在闭合系统中的演化,它是可逆的,保持量子态的相干性和规范化。酉演化在量子计算和量子算法中扮演了核心角色。
- 测量则是不可逆的过程,通常伴随着量子态的坍缩,并且结果具有随机性。测量改变了系统的状态,使其坍缩到某个测量本征态。
它们在量子计算中的联系是,量子算法通过一系列酉操作来操控量子态,最后通过测量获取结果。酉演化负责量子计算中的计算过程,而测量则负责读取最终的输出。
量子噪声
迹与偏迹(见附录三)
单量子比特操作的几何图像(使用布洛赫球描述,较为直观)
比特翻转与相位翻转(见附录一)
常见的量子噪声有:
退极化信道(Depolarizing Channel)
退极化信道是一种描述量子态受外部噪声影响而变得“混乱”的噪声模型。在这种模型中,量子比特的状态有一定概率被完全破坏,变成最大混合态,而保持其原本状态的概率则较大。


相位阻尼信道(Phase Damping Channel)
相位阻尼信道(也称为相位衰减信道)是一种描述量子态的相位信息在环境相互作用中逐渐丢失的过程。它反映了量子比特的相干性(即量子叠加态中不同分量的干涉效果)如何在与环境相互作用中衰减。


振幅阻尼信道(Amplitude Damping Channel)
振幅阻尼信道是一种描述能量耗散的噪声模型,主要用于描述系统中的激发态逐渐弛豫到基态的过程。该信道模拟了系统通过与环境的能量交换,使量子比特的振幅逐渐减小的过程。


三种噪声的总结

小结
算子和表示:一个开放系统的行为可以被建模为:
其中是操作元,如果量子操作是保迹的,那么满足
量子操作的环境模型:一个保迹的量子操作总能被看作是通过系统与初始时不关联的环境的酉相互作用产生,反过来也一样。非保迹量子操作也可能类似地处理,除了一个额外的施加在系统与环境的复合体上的投影操作,不同的结果对应于不同的非保迹量子操作。
附录
1.比特反转和相位反转是什么?
比特反转(Bit Flip)和相位反转(Phase Flip)是量子计算中的两种常见的量子错误类型,它们代表了量子比特(qubit)在不同方面的状态变化。两者的主要区别在于它们对量子比特状态的影响方式不同。
比特反转(Bit Flip)
比特反转是指量子比特的经典状态发生翻转。它类似于经典计算中的位翻转(0和1之间的切换)。在量子比特的情况下,量子比特的状态可以描述为: 如果发生比特反转错误,量子比特的状态从∣0〉变为∣1〉,或从∣1〉变为∣0〉。对于任意叠加态,这种翻转作用在经典比特部分上。例如:
- 如果量子比特的状态是∣0〉,比特反转会将其变为∣1〉;
- 如果量子比特的状态是∣1〉,比特反转会将其变为∣0〉。
数学上,比特反转可以用X门(Pauli-X门,类似于经典的NOT门)来表示:
相位反转(Phase Flip)
相位反转则影响量子比特的相位信息,而不改变其经典状态。在量子比特的状态表示中,相位是影响叠加态的干涉效果的关键因素。相位反转会使量子比特的相位发生翻转,例如将叠加态中的某个项的符号取反。
相位反转主要影响量子态中的∣1〉分量,而不会改变∣0〉分量。比如: 相位反转错误会将量子比特的状态变为:
比特反转是一个状态的改变,而相位反转时符号的改变。
2.如何纯化混合态?
量子态通常可以分为两种类型:纯态和混合态。纯态是完全确定的量子态,可以用一个单一的态矢量描述;而混合态则是多种量子态的概率混合,不能简单地用一个态矢量描述,而是用密度矩阵来表示。纯化(Purification)是一种将混合态扩展到一个更高维度的系统(通常是通过引入辅助系统)将其转换为纯态的方法。
混合态与纯态的区别
-
纯态:量子系统的状态完全确定,可以用一个态矢量
来描述。
对应的密度矩阵:
-
混合态:量子系统处于多个纯态的概率混合中,无法用单一的态矢量描述。通常用密度矩阵来表示:
其中,
是各个纯态,
是对应纯态的概率
纯态即混合态,包含基态的∣0〉和∣1〉,这两个态构成了量子比特的标准基,在物理上可以表示不同状态,例如粒子的上旋和下旋,光子的垂直偏振和水平偏振。
纯化的基本思想
纯化的目标是将混合态提升到一个更高维的纯态,即通过引入一个额外的辅助系统,使得整个系统—包括原始系统和辅助系统—处于一个纯态,而原始系统单独来看依然是混合态。这样做的意义是,通过将混合态嵌入一个更大的系统中,我们可以用纯态的数学工具(如态矢量)来处理混合态。
具体纯化方法

纯化的例子

3. 为什么需要密度算子,为什么需要取偏迹
密度算子(density operator)和偏迹(partial trace)是用于描述和处理复合量子系统及其子系统的重要工具。用于区分纯态和混合态以及分析量子系统与环境的交互。
1.1 描述混合态
在某些情况下,量子系统并不处于一个纯态,而是处于多个可能态的概率混合状态。例如,如果一个系统可能以50%的概率处于∣0〉,以50%的概率处于∣1〉,这不是一个单纯的叠加态,而是一个混合态。此时,单纯的态矢量无法描述这个系统的状态,因为系统没有确定的量子相干性。
为了表示这种混合态,我们需要用密度矩阵(或密度算子)ρ来描述。密度矩阵不仅可以描述纯态,也可以描述混合态:
- 纯态:
- 混合态:
混合态通常出现在如下场景:
- 不完全信息:当我们对系统的精确状态没有完全了解时,用密度算子表示不同可能量子态的概率组合。
- 与环境的纠缠:当系统与外部环境纠缠时,系统本身的状态是混合态。
1.2 更一般的量子态描述
密度算子不仅能够处理混合态,还能够更清晰地描述量子态的统计属性。它的优点包括:
- 概括性:它可以同时处理纯态和混合态。
- 期望值计算:通过密度矩阵,可以计算系统的任何可观测量的期望值,公式为:
- 其中O是可观测量,ρ是系统的密度矩阵。
1.3 热力学和开放量子系统
在开放量子系统(与环境交互的系统)或热力学系统中,系统通常处于混合态。由于外部环境的作用,系统的状态不能用一个确定的纯态表示。这时,密度算子可以描述系统在外部扰动下的状态。
为什么需要取偏迹?
偏迹(partial trace)通过对复合系统中某些自由度“忽略”或“消去”,来得到子系统的状态。
量子系统往往与其他系统发生纠缠或复合。例如,系统A和环境B处于纠缠态时,整个系统的状态是一个复合态。但在很多情况下,我们只关心系统A的状态,而不关心系统B。
在这种情况下,系统A的状态就是通过对复合系统的密度矩阵取系统B的偏迹得到的:
例如当A和B系统纠缠,

系统A的状态是一个混合态,而不是纯态。这说明量子纠缠导致了子系统状态的混合性。
4.量子过程层析
量子过程层析是一种用于完全表征未知量子操作(或量子过程)的技术。它的目的是通过实验测量,确定量子操作(例如量子门或量子演化)的完整数学描述。
量子过程表示

量子过程层析的基本步骤
1.1 选择输入态
为了完全表征量子过程 ,首先要准备一组不同的输入量子态。这组量子态必须是该系统的线性完备集,即它们能完全张成系统的希尔伯特空间。对于一个 d 维的量子系统,一般需要准备
个不同的输入态。
对于单量子比特系统,可以选择以下常见的四个状态作为输入态:

对于多量子比特系统,输入态数量随着系统维度成平方增长。
1.2 作用量子操作
将每一个准备好的输入量子态送入待测的量子操作,经过量子操作后,这些输入态将演化为新的量子态
。
1.3 测量输出态
在得到每一个输入态的输出态后,通过量子态层析(QST)技术对这些输出态进行测量,确定输出态的密度矩阵。对于每一个输入态 ,测量其对应的输出态
。
1.4 重构量子过程
通过分析所有输入态和对应输出态的信息,利用以下公式进行求解,重构量子过程 :
其中, 是重构的过程矩阵(Choi矩阵),σm和 σn是一组线性完备的算符基(例如 Pauli 基)。
通过测量不同输入态和输出态的结果,求解过程矩阵,从而完全描述该量子操作的行为。
2. 过程矩阵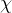
过程矩阵是量子过程
的一个完全描述,它包含了该量子操作如何作用于所有可能的输入量子态的信息。它的维度是
,其中 dd是系统的维度。例如,对于一个单量子比特系统,
是一个4×4 的矩阵。
在量子过程层析中,测量实验的数据用于估计矩阵中的各个元素。得到
矩阵后,我们就可以通过它来预测该量子过程对任意输入态的作用。
量子过程层析一些主要的挑战包括:
- 输入态的制备:需要能够精确地制备一组线性完备的输入态。
- 测量误差:由于测量噪声,输出态的测量可能不够精确。
- 维度扩展:对于高维量子系统,所需的输入态和测量数量迅速增长,使得实验的复杂度急剧上升。