太原理工大学计算机控制技术实验之积分分离PID控制实验

实验原理

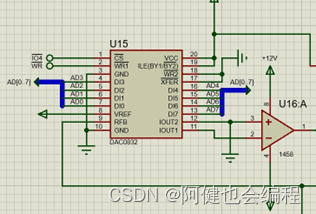
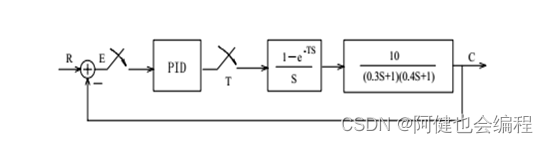上图是一个典型的PID 闭环控制系统方框图，其硬件电路原理及接线图可设计如下，图中画“○”的线需用户在实验中自行接好，对象需用户在运放单元搭接。
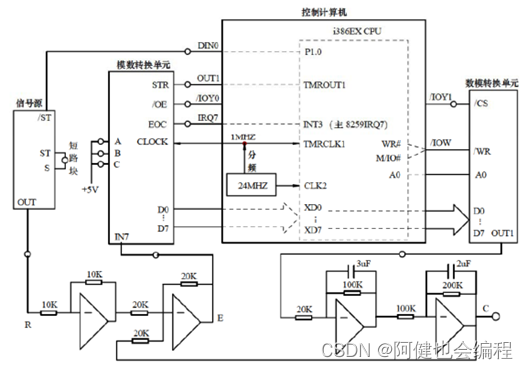上图中，控制计算机的“OUT1”表示386EX 内部1＃定时器的输出端，定时器输出的方波周期＝定时器时常，“IRQ7”示386EX 内部主片8259 的7号中断，用作采样中断，“DIN0”表示386EX 的I/O 管脚P1.0，在这里作为输入管脚用来检测信号是否同步。这里，系统误差信号E 通过模数转换单元“IN7”端输入，控制机的定时器作为基准时钟 (初始化为10ms)，定时采集“IN7”端的信号，并通过采样中断读入信号E 的数字量，并进行PID计算，得到相应的控制量，再把控制量送到数模转换单元，由“OUT1”端输出相应的模拟信号，来控制对象系统。
本实验中，采用位臵式PID算式。在一般的PID控制中，当有较大的扰动或大幅度改变给定值时，会有较大的误差，以及系统有惯性和滞后，因此在积分项的作用下，往往会使系统超调变大、过渡时间变长。为此，可采用积分分离法PID 控制算法，即：当误差e(k)较大时，取消积分作用；当误差e(k)较小时才将积分作用加入。图3是积分分离法PID控制实验的参考程序流程图。

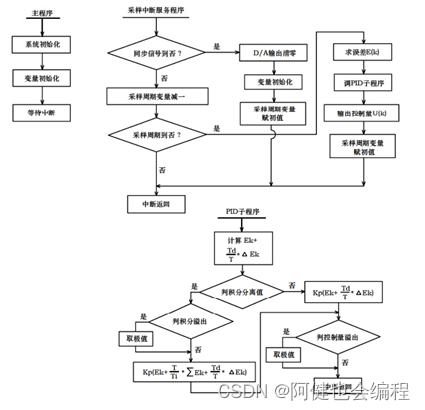
实验参考程序：请参照随机软件中的example 目录中的ACC3-2-1.ASM。
为了便于实验参数的调整，下面讨论PID 参数对系统性能的影响：
(1)增大比例系数KP一般将加快系统的响应，在有静差的情况下有利于减小静差。但过大的比例系数会使系统有较大的超调，并产生振荡，使系统稳定性变坏。
(2)增大积分时间参数TI 有利于消除静差、减小超调、减小振荡，使系统更加稳定，但系统静差的消除将随之减慢。
(3)增大微分时间参数TD 有利于加快系统响应，使超调量减小，系统稳定性增加，但系统对扰动的抑制能力减弱，对扰动有较敏感的响应。
在调整参数时，可以使用凑试法。参考以上参数对控制过程的影响趋势，对参数实行“先比例，后积分，再微分”的步骤。
(1)首先整定比例部分。将比例系数KP 由小变大，并观察相应的系统响应，直到响应曲线超调小、反应快。如果系统没有静差，或者静差小到允许的范围内，那么只需比例调节器即可。
(2)如果在比例调节的基础上系统的静差不能满足要求，则须加入积分作用。整定时首先置积分时间TI 为一较大值，并将第一步整定得到的比例系数KP 缩小 (如80％)，然后减小积分时间，使静差得到消除。如果动态性能 (过渡时间短) 也满意，则需PI 调节器即可。
(3)若动态性能不好，则需加入微分作用。整定时，使微分时间TD 从0 变大，并相应的改变比例系数和积分时间，逐步凑试，直到满意结果。
由于PID 三个参数有互补作用，减小一个往往可由几个增大来补偿，因此参数的整定值不唯一，不同的参数组合完全有可能得到同样的效果。

实验内容

1、参考流程图3编写实验程序，检查无误后编译、链接。
2、按照实验线路图2接线，检查无误后开启设备电源。


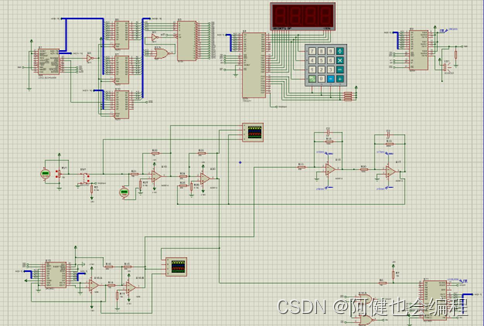
3、调节信号源中的电位器及拨动开关，使信号源输出幅值为2V，周期10S 的方波。确定系统的采样周期以及积分分离值。
4、装载程序，将全局变量TK(采样周期)、EI(积分分离值)、KP(比例系数)、TI(积分系数)和TD(微分系数)加入变量监视，以便实验过程中观察和修改。
5、运行程序，将积分分离值设为最大值7FH(相当于没有引入积分分离)，用示波器分别观测输入端R和输出端C。
6、如果系统性能不满意，用凑试法修改PID参数，直到响应曲线满意，并记录响应曲线的超调量和过渡时间。
7、修改积分分离值为20H，记录此时响应曲线的超调量和过渡时间，并和未引入积分分离值时的响应曲线进行比较。
8、将6和7中的较满意的响应曲线分别保存，在画板、PHOTOSHOP中处理后粘贴到WORD中，方便形成实验报告。

实验结果

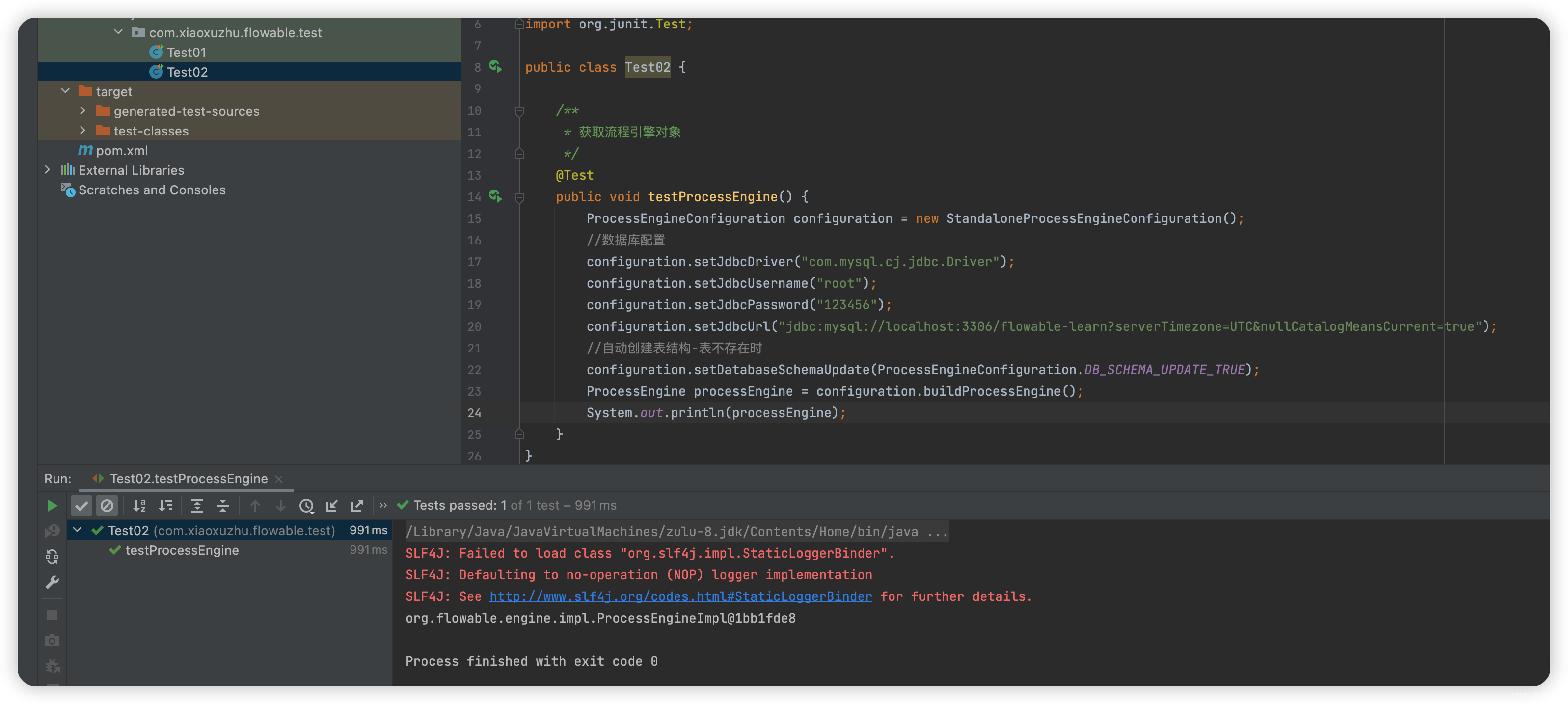
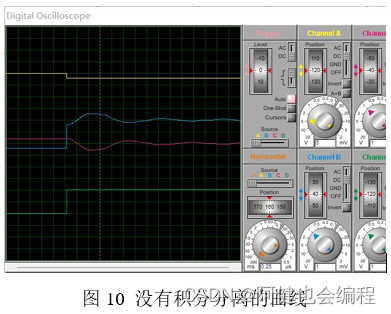
（1）修改积分分离值为7FH(相当于没有引入积分分离)，运行仿真，观察到波形如下程序中积分分离值变量是IBAND，所以需要将这个变量改成7FH

程序中会进行偏差幅值判断if(ABS(EK)>IBAND),就会进入积分分离的程序

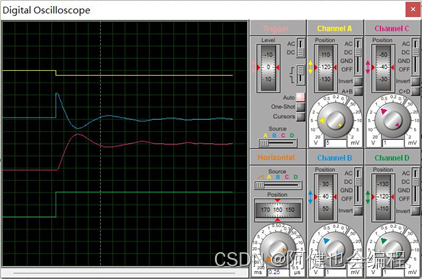
黄色：反相后的阶跃信号曲线
蓝线：偏差信号曲线
红线：最终的输出信号曲线
绿线：给定的阶跃信号曲线

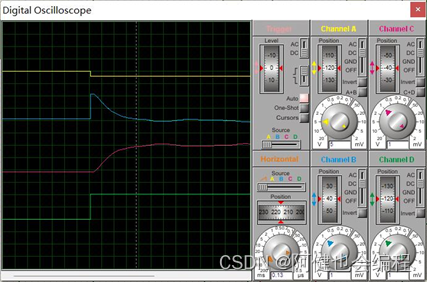
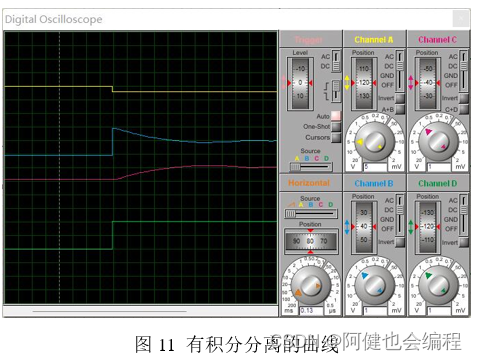
（2）修改积分分离值为20H(相当于引入积分分离)，运行仿真，观察到波形如下程序中积分分离值变量是IBAND，所以需要将这个变量改成20H

思考题

1) 试结合实验原理图和模电知识，根据组成被控对象的两个运算放大器及电阻电容参数，推导对象的传递函数，需要过程
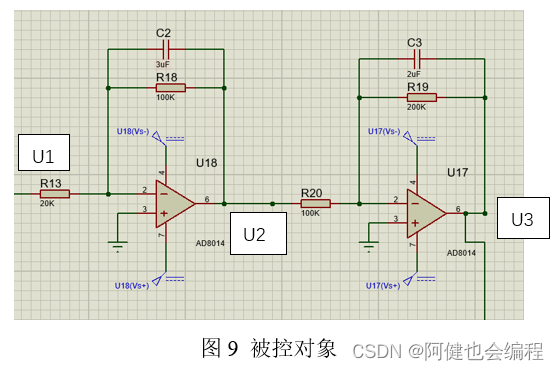
U_1/R_13 =-(U_2/R_18 +C_2 (dU_2)/dt)
S变换后
U_1/R_13 =-(U_2/R_18 +C_2 U_2 s)
则, U_2=1/(R_13 C_2 s+R_13/R_18 ) U_1
代入R_13=20k,R_18=100k,C_2=3uF，则
U_2/U_1 =5/(0.3s+1)
同理，得
U_2/R_20 =-(U_3/R_19 +C_3 U_3 s)
代入R_20=100k,R_19=200k,C_3=2uF，则
U_3/U_2 =2/(0.4s+1)
所以，最终传函为G（s）= U_3/U_1 = U_3/U_2 *U_2/U_1 = 10/((0.3s+1)(0.4s+1))

2)试将第二个运算放大器的电容参数改为3微法，重新推导对象传递函数，并进行试验过程。
将第二个运算放大器的电容参数改为3微法,即C_3=3uF，则重新带入，得

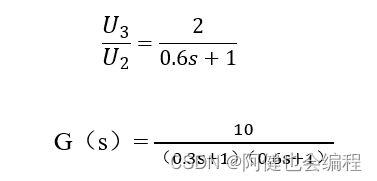
3) 实验中采样周期对PID控制结果有什么影响？
采样周期越小，数字模拟越精确，控制效果越接近连续控制。对大多数算法，缩短采样周期可使控制回路性能改善，但采样周期缩短时，频繁的采样必然会占用较多的计算工作时间，同时也会增加计算机的计算负担，而对有些变化缓慢的受控对象无需很高的采样频率即可满意地进行跟踪，过多的采样反而没有多少实际意义。
但是采样周期过大，会因为采样点过稀而丢失被采集的模拟量中的重要信息，会产生较大误差，会使PID控制失效。

4）积分分离阈值对超调量有什么影响？
当误差值比较大时，取消积分作用，以免由于积分作用使得系统稳定性降低，超调量增大；当被控量接近目标值时（即误差较小时），引入积分控制，以消除净差，提高控制精度。
如果阈值取得过大，达不到积分分离作用，超调量依旧很大，如果阈值取得过小，则只有PD控制，那么系统超调减小了，但是系统无法消除静差。