文章链接:https://arxiv.org/pdf/2410.04671
项目链接:https://github.com/MiracleDance/CAR
亮点直击
- CAR是首个为自回归模型家族设计的灵活、高效且即插即用的可控框架。
- CAR基于预训练的自回归模型,不仅保留了原有的生成能力,还能在有限资源的情况下实现可控生成——所用数据量不到预训练所需数据的10%。
- 设计了一个通用框架来捕捉多尺度的控制表示,这些表示具有鲁棒性,并能无缝集成到预训练的基础模型中。
- 大量实验表明,CAR在各种条件信号下实现了精确的细粒度视觉控制。CAR有效地学习了这些条件的语义,能够在训练集中未见过的类别上实现鲁棒的泛化。

总结速览
解决的问题:
当前的视觉生成模型主要有两种技术路径:扩散模型和自回归模型。扩散模型在生成控制上表现出色,但自回归模型虽然具备强大的生成能力和可扩展性,控制性和灵活性方面仍然未被充分探索。
提出的方案:
提出了一种名为可控自回归建模(CAR) 的全新框架,该框架可作为插件,整合条件控制机制到多尺度潜变量建模中,允许在预训练的视觉自回归模型中进行高效的控制生成。CAR逐步细化并捕捉控制表示,并将其注入到预训练模型的每个自回归步骤中,以引导生成过程。
应用的技术:
- 多尺度潜变量建模:用于捕捉和细化控制表示。
- 预训练视觉自回归模型:在预训练模型的基础上注入控制,逐步指导生成。
- 条件控制机制:整合到自回归生成的每个步骤中,以实现细粒度控制。
达到的效果:
- 在各种条件下实现了出色的控制能力。
- 在图像质量上优于以往的方法。
- 与预训练模型相比,CAR在实现良好泛化能力的同时显著减少了训练资源需求。
- CAR是首个针对预训练自回归视觉生成模型的控制框架。
方法
可控自回归建模(CAR),旨在探索自回归模型在可控图像生成任务中的潜力。将任务定义如下:给定一个条件控制图像 C ∈ R 3 × H × W C \in R^{3 \times H \times W} C∈R3×H×W,其中 H H H 和 W W W 代表图像的高度和宽度,我们的目标是生成一个与指定视觉条件对齐的可控图像 I ∈ R 3 × H × W I \in R^{3 \times H \times W} I∈R3×H×W。总体目标可以表述为建模条件分布 p ( I ∣ C ) p(I | C) p(I∣C)。
首先介绍视觉自回归建模中“下一尺度预测”范式的基础概念。接着解释了CAR框架如何通过多尺度潜变量建模控制视觉生成。通过应用贝叶斯推理,我们识别出CAR的学习目标是获取一个鲁棒的控制表示。最后详细讨论了控制表示的表达以及网络优化策略。
自回归建模的基础知识
传统的自回归模型采用“下一个token预测”的方法,将图像离散化并展平为序列 ( x 1 , x 2 , . . . , x T ) (x_1, x_2, ..., x_T) (x1,x2,...,xT),其中 T T T 是图像特征图的高度和宽度的乘积。每个token x t x_t xt 基于前面的tokens ( x 1 , x 2 , . . . , x t − 1 ) (x_1, x_2, ..., x_{t-1}) (x1,x2,...,xt−1) 进行预测。最终的token序列被量化并解码以生成图像。
然而,最近的一项研究(Tian et al., 2024)指出,这种范式可能导致数学不一致性和结构退化,对于生成高度结构化的图像而言,这并非最优。为了解决这个问题,它引入了一种全新的视觉自回归建模范式(VAR),从“下一个token预测”转变为“下一尺度预测”。在VAR中,每个单元预测不同尺度下的完整token图。生成过程从 1 × 1 1 \times 1 1×1 尺度的token图 r 1 r_1 r1 开始,VAR依次预测一系列多尺度token图 ( r 2 , . . . , r K ) (r_2, ..., r_K) (r2,...,rK),分辨率逐渐增加。生成过程表达为:
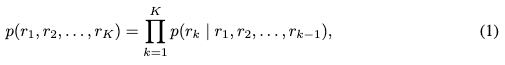
其中 r k ∈ [ V ] h k × w k r_k \in [V]^{h_k \times w_k} rk∈[V]hk×wk 代表第 k k k 级的token映射,尺寸为 h k h_k hk 和 w k w_k wk,并且基于之前的token映射 ( r 1 , r 2 , . . . , r k − 1 ) (r_1, r_2, ..., r_{k-1}) (r1,r2,...,rk−1) 进行条件预测。 r k r_k rk 中的每个token都是从VQVAE码本 V V V 中选取的索引,VQVAE通过多级量化进行训练,并在不同尺度之间共享。
可控视觉自回归建模
如下图2所示,CAR框架通过建模条件分布 p ( I ∣ C ) p(I | C) p(I∣C) 来实现可控图像生成。目标是最大化 p ( I ∣ C ) p(I | C) p(I∣C) 的似然,确保生成的图像 I I I 符合由条件图像 C C C 指定的视觉条件。
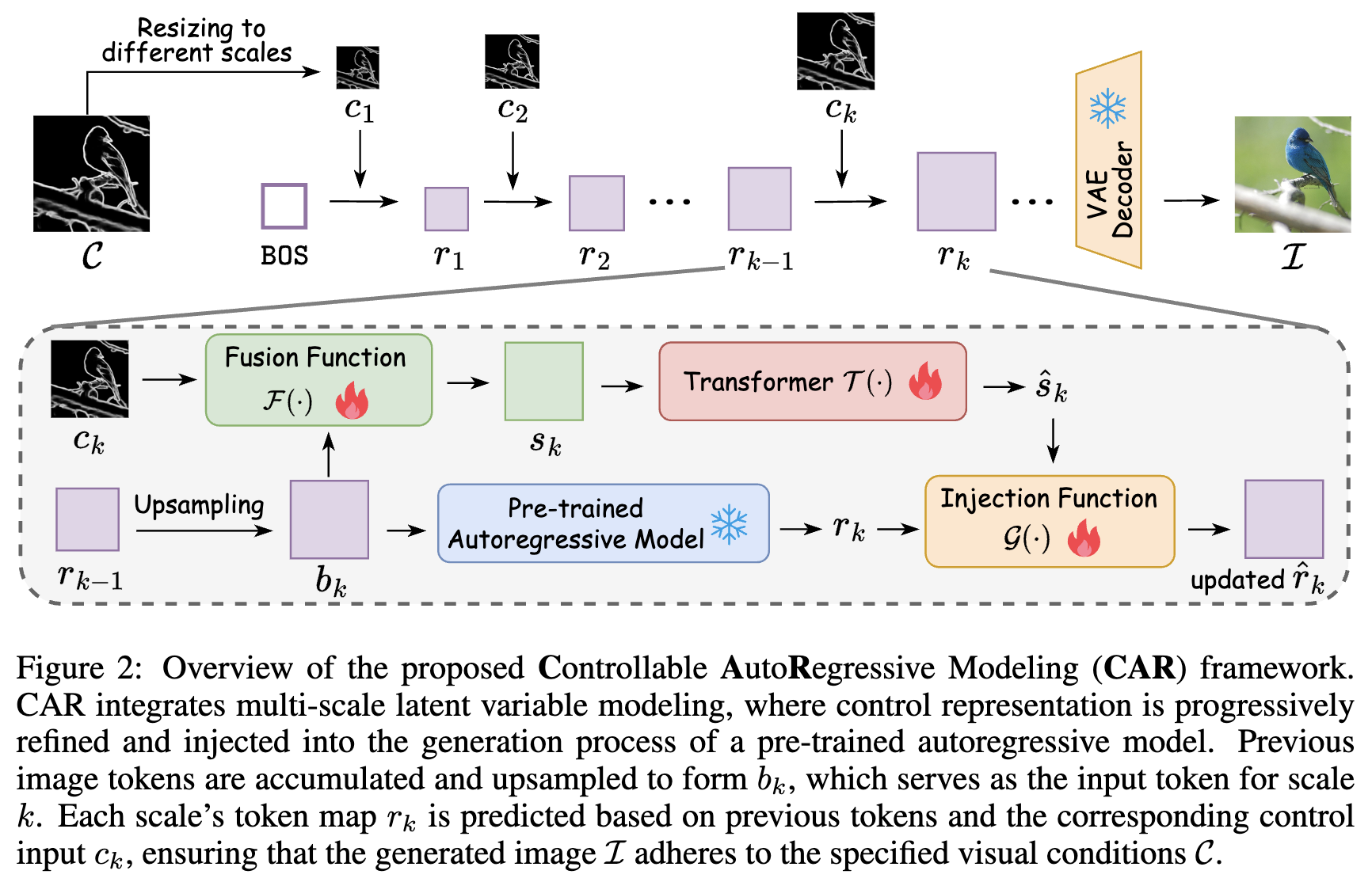
遵循VAR的“下一尺度预测”范式,CAR模型采用了多尺度潜变量框架,其中每个尺度的潜变量(token图)捕捉逐步更高分辨率的图像结构。控制信息提供了额外的观测,用于辅助推断每个尺度的潜变量。
多尺度条件概率建模
假设潜变量框架中共有
K
K
K 个尺度,CAR模型以多尺度的方式生成图像
I
I
I,通过在每个尺度上将条件分布
p
(
I
∣
C
)
p(I | C)
p(I∣C) 分解为条件概率的乘积来实现:
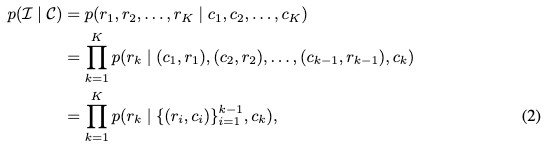
其中 r k ∈ R h k × w k r_k \in \mathbb{R}^{h_k \times w_k} rk∈Rhk×wk 是第 k k k 尺度的图像token图,而 c k ∈ R h k × w k c_k \in \mathbb{R}^{h_k \times w_k} ck∈Rhk×wk 是从控制图像 C C C 中派生的对应控制图。每个token图 r k r_k rk 的生成条件是之前的token图 ( r 1 , r 2 , . . . , r k − 1 ) (r_1, r_2, ..., r_{k-1}) (r1,r2,...,rk−1) 以及控制信息 ( c 1 , c 2 , . . . , c k ) (c_1, c_2, ..., c_k) (c1,c2,...,ck)。这种多尺度条件建模确保了每个尺度的控制信息在递归和分层的过程中引导生成过程,逐步细化图像token图的潜在表示。
后验近似
在CAR框架中,如公式2所示,前一尺度的图像和控制token图
(
{
r
i
,
c
i
}
i
=
1
k
−
1
)
(\{r_i, c_i\}_{i=1}^{k-1})
({ri,ci}i=1k−1) 以及当前尺度的控制token图
c
k
c_k
ck 构成了当前尺度图像token图的后验近似。这意味着
r
k
r_k
rk 是通过利用这个后验近似的信息生成的。从贝叶斯的角度来看,CAR模型的目标是在每个尺度上,给定控制信息,近似图像token的后验分布:
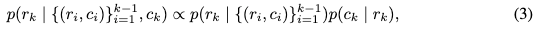
其中, p ( r k ∣ { ( r i , c i ) } i = 1 k − 1 ) p(r_k | \{(r_i, c_i)\}_{i=1}^{k-1}) p(rk∣{(ri,ci)}i=1k−1) 表示从之前的token图中跨尺度学习到的自回归先验, p ( c k ∣ r k ) p(c_k | r_k) p(ck∣rk) 则表示在给定当前图像token图 r k r_k rk 的情况下观察到控制token图 c k c_k ck 的似然。
基于上述贝叶斯推理,可以明确识别出CAR的学习目标是优化 c k c_k ck,使得该控制表示与图像表示 r k r_k rk 对齐。该目标可以通过神经网络进行学习,由提供的图像数据集中的真实 r k r_k rk 进行监督,使网络逐步逼近后验分布。
控制表示和优化
控制表示表达
VAR 从之前所有尺度积累图像token
{
r
i
}
i
=
1
k
−
1
\{r_i\}_{i=1}^{k-1}
{ri}i=1k−1,并对其进行插值以匹配分辨率
h
k
×
w
k
h_k \times w_k
hk×wk,然后形成用于第
k
k
k 尺度推理的输入,记为
b
k
b_k
bk。在CAR框架中,在每个尺度
k
k
k,通过融合输入的图像token图
b
k
∈
R
h
k
×
w
k
×
d
b_k \in \mathbb{R}^{h_k \times w_k \times d}
bk∈Rhk×wk×d 和控制图
c
k
∈
R
h
k
×
w
k
×
d
c_k \in \mathbb{R}^{h_k \times w_k \times d}
ck∈Rhk×wk×d 来注入控制信息,从而形成一个组合表示。

其中 F ( ⋅ ) F(\cdot) F(⋅) 是一个由参数 θ F \theta_F θF 表示的融合函数。该融合机制确保 s k s_k sk 包含了生成的图像特征和控制条件。通过利用 s k s_k sk 来预测 r k r_k rk,将控制信息纳入生成过程中,确保生成的token图符合控制条件 c k c_k ck,从而提供细粒度的引导。
为了确保有效提取控制表示并整合控制信息,融合后的表示 s k s_k sk 被向量化,并通过一系列Transformer层进行变换,产生精炼的条件先验,以引导每个尺度 k k k 的图像生成。形式上, s k s_k sk 通过学习到的映射 T ( ⋅ ) T(\cdot) T(⋅) 转化为向量化表示 s ^ k \hat{s}_k s^k,具体如下:

其中 T ( ⋅ ) T(\cdot) T(⋅) 由CAR的Transformer参数 θ T \theta_T θT 表示,它被设计为与VAR的Transformer并行的分支。 T ( ⋅ ) T(\cdot) T(⋅) 中的块对向量化的控制表示执行自注意力操作,通过建模控制信息中的依赖关系,提取相关的条件先验。
一旦提取出精炼的条件先验 s ^ k \hat{s}_k s^k,它将被注入到由预训练的VAR预测的图像token图 r k r_k rk 中, r k r_k rk 代表第 k k k 尺度的潜在图像特征。该注入过程通过一个由参数 θ G \theta_G θG 表示的注入函数 G ( ⋅ ) G(\cdot) G(⋅) 来实现, G ( ⋅ ) G(\cdot) G(⋅) 结合了 s ^ k \hat{s}_k s^k 和 r k r_k rk,确保控制信息调制生成的图像token。

其中, r ^ k \hat{r}_k r^k 表示更新后的token图,结合了控制信息。该机制使模型能够在多尺度控制信息的基础上逐步调节生成过程,从而生成在各个尺度上连贯并符合外部视觉条件 C C C 的图像。
网络优化
为了使生成的图像
I
I
I 与控制条件
C
C
C 对齐,我们最小化模型的条件分布
p
(
I
∣
C
;
θ
c
a
r
)
p(I | C; \theta_{car})
p(I∣C;θcar) 与真实数据分布
p
data
(
I
∣
C
)
p_{\text{data}}(I | C)
pdata(I∣C) 之间的Kullback-Leibler (KL) 散度 (Kullback & Leibler, 1951):
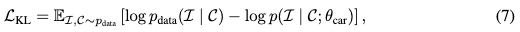
其中, θ c a r \theta_{car} θcar 表示我们CAR框架中的可学习参数,具体为 { θ F , θ T , θ G } \{\theta_F, \theta_T, \theta_G\} {θF,θT,θG}。由于 p data ( I ∣ C ) p_{\text{data}}(I | C) pdata(I∣C) 相对于 θ c a r \theta_{car} θcar 是常数,最小化 L K L L_{KL} LKL 相当于最大化对数似然 log p ( I ∣ C ; θ c a r ) \log p(I | C; \theta_{car}) logp(I∣C;θcar)。
利用融合后的表示 s k s_k sk,条件分布 p ( I ∣ C ; θ c a r ) p(I | C; \theta_{car}) p(I∣C;θcar) 可以被分解为:
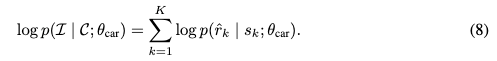
最大化这个对数似然函数的过程确保生成的token图 r ^ k \hat{r}_k r^k 与真实的 r k r_k rk 紧密匹配,同时与之前的token保持一致,并符合封装在 s k s_k sk 中的控制条件。这一过程有助于学习更有效的控制表示,如在方程3中的后验近似所概述的,确保生成的图像遵循控制条件 C C C 的同时保留预训练VAR的原始生成能力。
实验
实验设置
模型架构设计
作者采用预训练的VAR作为基础模型,在训练过程中对其进行冻结,以保留其生成能力并减少训练成本。对于可学习模块
{
θ
F
,
θ
T
,
θ
G
}
\{\theta_F, \theta_T, \theta_G\}
{θF,θT,θG},尝试了多种选择,并根据实验结果选择最佳设计方案。对于融合函数
F
(
⋅
)
F(\cdot)
F(⋅),使用卷积编码器从控制输入
c
k
c_k
ck 中提取语义特征,并将其添加到基础模型输入
b
k
b_k
bk 中。对于
T
(
⋅
)
T(\cdot)
T(⋅),设计了一系列类似于GPT-2的Transformer模块,其深度为预训练基础模型的一半。对于
G
(
⋅
)
G(\cdot)
G(⋅),通过连接将
s
^
k
\hat{s}_k
s^k 注入基础模型输出
r
k
r_k
rk 中,随后应用LayerNorm来规范化两个领域特征的分布,并进行线性变换以调整通道维度。
数据集
在 ImageNet数据集上进行实验。首先,为训练集伪标记了五个条件:Canny 边缘、深度图、法线图、HED 图和草图,允许 CAR 在不同的条件控制下分别进行训练。从总共 1000 个类别中随机选择 100 个用于训练 CAR,并在剩余的 900 个未见类别上进行评估,以评估其可泛化的可控性。
评估指标
利用 Fréchet Inception Distance (FID)、Inception Score (IS)、精准度和召回率指标来评估生成结果的质量。还与现有的可控生成方法(如 ControlNet和 T2I-Adapter)比较推理速度。
训练细节
将预训练的 VAR 深度设置为 16、20、24 或 30,并使用 VAR 的前半部分的权重初始化控制 Transformer
T
(
⋅
)
T(\cdot)
T(⋅),以加速收敛。CAR 模型在 8 个 NVIDIA V100 GPU 上训练 100 轮,推理速度在单个 NVIDIA 4090 GPU 上进行评估。
定量评估
与以前方法的比较
将 CAR 模型与两个经典的可控生成基线 ControlNet 和 T2I-Adapter 进行了比较。为确保公平,我们在 ImageNet 数据集上重新训练了这两个模型,并对每个模型在所有五个条件注释上分别进行训练。如下表 1 所示,CAR 显示出显著的改进,FID 分别在 Canny、深度、法线、HED 和草图条件下减少了 3.3、2.3、2.3、3.0 和 5.1,相较于 ControlNet。IS 指标也观察到类似的改进。将这些收益归因于自回归模型的最新进展,这些模型通过在生成过程中逐步扩大分辨率,超越了扩散模型的图像生成能力。除了图像质量外,还比较了推理速度,CAR 的速度比 ControlNet 和 T2I-Adapter 快五倍以上,进一步凸显了 CAR 在实际应用中的效率优势。总体而言,这些令人鼓舞的定量结果表明,CAR 可以作为一种比基于扩散模型的 ControlNet 更高效、可扩展的可控生成范式。
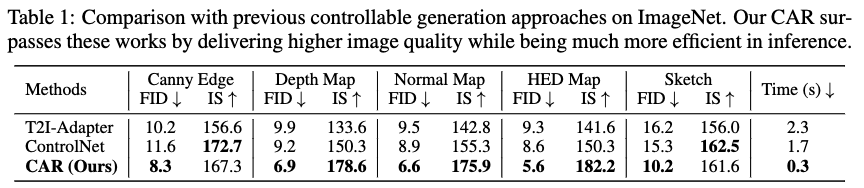
不同类型条件的评估值得注意,HED 图、深度图和法线图显示出相对较优的指标,这可能归因于输入条件的清晰性和明确的目标。这些因素为模型提供了更精确的指导,提升了高质量图像的生成。相比之下,草图条件往往比较简单,仅由基本轮廓构成,视觉细节较少,使其可控性较差,导致模型生成更自由。这可能导致图像质量波动。
规模法则
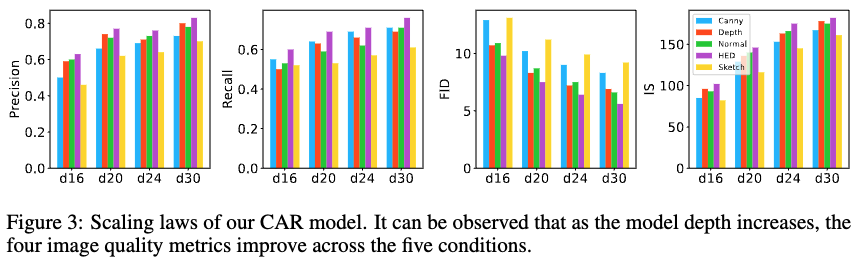
评估 CAR 模型在其深度增加时的图像质量。如下图 3 所示,随着模型深度的增加,CAR 在五种不同条件下生成更高质量的图像,表现出更低的 FID 指标以及更高的 IS、精准度和召回率,这与自回归生成建模的规模法则一致。在 HED 图、深度图和法线图中观察到最高的指标,而 Canny 边缘和草图则相对较低,这与表 1 的观察结果一致。
用户研究
研究者们邀请了 30 位参与者进行用户研究,以评估CAR 在与之前的方法 ControlNet 和 T2I-Adapter 的生成性能比较。对于五种类型的条件,输入 30 张条件图像,并为每种方法生成相应的结果,每种方法生成 150 个结果。对于每个条件输入,参与者需要根据三个标准选择最佳结果:1)图像质量,2)条件保真度,3)图像多样性。如下表 2 所示,CAR 在这三个方面均优于 ControlNet 和 T2I-Adapter,证明了所提出的可控自回归建模的有效性。

消融研究
整体可控性和图像质量
下图 4 展示了CAR 模型根据给定的条件控制生成高质量和多样化的结果。各种条件输入的视觉细节在生成的图像中得到了有效反映,确保了图像与其对应条件之间的强对齐。值得注意的是,展示的类别不在训练期间使用的 100 个类别之内,但 CAR 仍然能对这些未见类别实现精确控制,这表明CAR 学会了从给定的条件控制中提取一般语义信息,而不是对训练集进行过拟合。这一优势突显了CAR 框架的跨类别泛化能力和强大的可控性。

数据分布分析
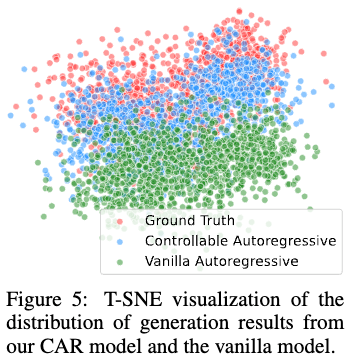
从数据分布的角度分析 CAR 的可控性。具体而言,HED 图被用作一种条件,引导图像生成过程,这一条件是从真实图像中提取的。我们采用一种不可控的传统自回归模型来生成比较样本。我们应用 t-SNE可视化所有生成图像的嵌入特征的前两个主成分。这些嵌入特征是使用 HED 图提取方法的主干提取的。
如下图 5 所示,传统自回归模型的生成分布与真实图像之间存在显著的不对齐,因为传统模型缺乏条件控制信息。相比之下,CAR 模型生成结果的分布与真实图像密切对齐,表明我们的样本准确捕捉了 HED 图的视觉细节,使 HED 嵌入特征更接近真实图像。这突显了CAR 模型增强了基于提供的条件控制 C 生成结果的可控性和准确性。
消融研究
在 ImageNet 验证集上进行消融研究,以探索 CAR 框架中每个组件(包括 F(·)、T(·) 和 G(·))不同功能选择的影响。
F(·) 的不同功能选择
探讨了不同方法引入条件控制 ck 以形成 sk 在 F(·) 中的影响。具体而言,比较了两种策略:1)使用 VAR 模型的预训练 VQ-VAE 编码器直接将条件图像映射到不同尺度的标记图;2)我们的方法,通过像素级调整条件图像至不同尺度,使用共享的可学习卷积编码器进行控制特征提取。
结果如表 3 所示,可学习编码器在 IS 分数上显示出显著改善,表明图像质量得到提升。我们推测,预训练的 VQ-VAE 编码器设计用于图像重建,可能无法有效捕捉图像语义,因此不太适合提取控制语义。图 6 的可视化结果也证明了这一点,使用 VQ-VAE 编码器的生成图像存在失真和质量差的问题。
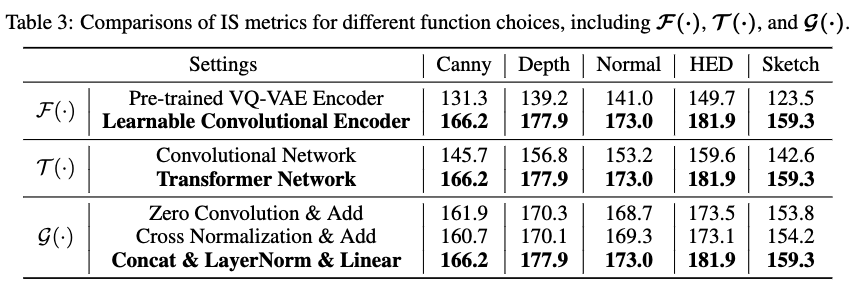

T(·) 的不同功能选择
我们设计了 T(·) 的编码器以提取准确有效的控制表示 ˆsk。具体而言,我们比较了两种架构:1)简单卷积网络;2)GPT-2 风格的 Transformer。下表 3 和图 6 显示,Transformer 相比简单卷积网络基线在图像质量上显著更高,这归因于其强大的表示能力。同时,基于 Transformer 的编码器与预训练自回归模型的架构相匹配,可能导致更接近的分布,增强后续注入过程。
G(·) 的不同功能选择
我们比较了不同的注入函数 G(·),在预训练自回归模型中将控制表示 ˆsk 注入图像表示 rk,以更新图像表示 ˆrk。具体而言,我们比较了三种技术:1)对控制表示应用零卷积(Zhang et al., 2023),然后加上控制和图像特征;2)应用交叉归一化,使用图像表示的均值和方差归一化控制表示,然后将这两个特征相加;3)我们的方法,将两个表示进行拼接,应用可学习的 LayerNorm 进行归一化,然后进行线性变换以调整通道维度。如上面表 3 所示,无论在加法之前是否应用零卷积和交叉归一化,添加图像和控制特征都会导致 IS 指标下降。这表明这些操作导致的图像质量降低,与我们的方法相比,生成结果在图像质量和自然性上表现较差。我们将此归因于两种不同领域表示的不兼容性。尽管交叉归一化试图对齐领域间的分布差异,但这种操作是不够的。因此,拼接这两个表示,再进行 LayerNorm,更有效地协调条件特征和主干特征,从而解决数据分布中的差异。
结论
本文提出了可控自回归建模(CAR),该模型建立了一种新颖的控制 VAR 生成的范式。CAR 捕捉了强大的多尺度控制表示,这些表示可以无缝集成到预训练的自回归模型中。实验结果表明,CAR 在可控性和图像质量方面均优于现有方法,同时降低了所需的计算成本。CAR 代表了自回归视觉生成的一个重要进展,为各种可控生成任务提供了一种灵活、高效且可扩展的解决方案。
讨论与未来工作
尽管所提出的 CAR 框架在可控视觉生成方面表现出色,但仍面临 VAR 模型固有的一些限制。具体而言,依赖于顺序token预测有时会限制模型的效率,特别是在处理长图像序列或需要在高分辨率下进行精细控制时。CAR 中使用的多尺度注入机制也可以扩展,以探索替代注入策略,例如基于注意力的或自适应注入,以进一步增强控制精度。此外,尽管当前设计在递归方式中优秀地注入了控制信号,但扩展框架以处理更复杂的任务,如视频生成,仍然是未来工作的一个开放挑战。
参考文献
[1] CAR: Controllable Autoregressive Modeling for Visual Generation