摘要
本文基于滑模控制、反步控制和传统PID控制,设计了针对四旋翼无人机的轨迹跟踪控制系统。通过对比这三种控制策略在四旋翼无人机轨迹跟踪中的表现,分析了各自的优缺点和适用场景。仿真结果表明,滑模控制具有更强的鲁棒性,反步控制在响应速度上具有优势,而传统PID控制方法相对简单易实现但精度略逊一筹。
理论
四旋翼无人机的运动控制是一个复杂的非线性系统问题,传统PID控制策略在某些线性场景下有着较好的效果,但在面对复杂轨迹跟踪任务时,受非线性因素和外界干扰影响较大。为了提高控制系统的鲁棒性和跟踪精度,本文引入了滑模控制和反步控制策略。
-
滑模控制:通过设计滑模面,使得系统状态能够快速到达并保持在该面上,进而实现对系统的不确定性和外部扰动的鲁棒控制。
-
反步控制:通过将控制目标逐步分解,逐步设计虚拟控制量,使系统从高阶逐步稳定到低阶,最终达到全局控制目标。
-
传统PID控制:经典的比例-积分-微分控制器,通过调整三个参数,调节系统的误差响应。
实验结果
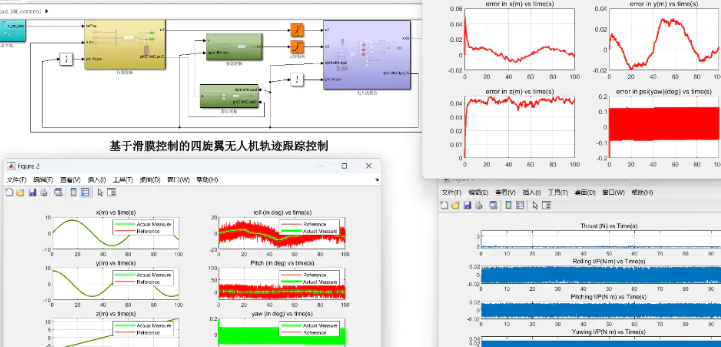
通过Matlab仿真,对比了三种控制策略的轨迹跟踪性能。以下为部分结果:
-
在X轴、Y轴和Z轴的轨迹跟踪精度对比中,滑模控制表现出了最小的误差波动,反步控制的误差次之,传统PID控制的误差相对较大。
-
反步控制在系统响应时间方面优于滑模控制,PID控制方法的响应时间相对较慢。
-
对于抗干扰能力,滑模控制具有显著优势,能够更好地应对外部扰动。
部分代码
% 四旋翼无人机轨迹跟踪PID控制仿真代码
% 定义系统参数
Kp = [1.2, 1.2, 1.5]; % 比例增益
Ki = [0.1, 0.1, 0.1]; % 积分增益
Kd = [0.3, 0.3, 0.3]; % 微分增益
% 初始化变量
X_ref = 10; Y_ref = 10; Z_ref = 10; % 参考轨迹
X = 0; Y = 0; Z = 0; % 初始位置
dt = 0.01; % 时间步长
t = 0:dt:10; % 仿真时间
% PID 控制器
for i = 1:length(t)
% 误差计算
e_x = X_ref - X(i);
e_y = Y_ref - Y(i);
e_z = Z_ref - Z(i);
% PID 控制计算
u_x = Kp(1) * e_x + Ki(1) * sum(e_x) * dt + Kd(1) * (e_x - X(i)) / dt;
u_y = Kp(2) * e_y + Ki(2) * sum(e_y) * dt + Kd(2) * (e_y - Y(i)) / dt;
u_z = Kp(3) * e_z + Ki(3) * sum(e_z) * dt + Kd(3) * (e_z - Z(i)) / dt;
% 更新位置
X(i+1) = X(i) + u_x * dt;
Y(i+1) = Y(i) + u_y * dt;
Z(i+1) = Z(i) + u_z * dt;
end
% 绘制结果
figure;
plot3(X, Y, Z);
xlabel('X'); ylabel('Y'); zlabel('Z');
title('PID控制的四旋翼无人机轨迹跟踪');
参考文献
❝
Slotine, J. J. E., & Li, W. (1991). Applied Nonlinear Control. Prentice-Hall.
Isidori, A. (1995). Nonlinear Control Systems. Springer.
Khalil, H. K. (2002). Nonlinear Systems. Prentice Hall.
Madani, T., & Benallegue, A. (2006). "Backstepping Control for a Quadrotor Helicopter". In IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS).
Utkin, V. I. (1992). Sliding Modes in Control Optimization. Springer-Verlag.
(文章内容仅供参考,具体效果以图片为准)