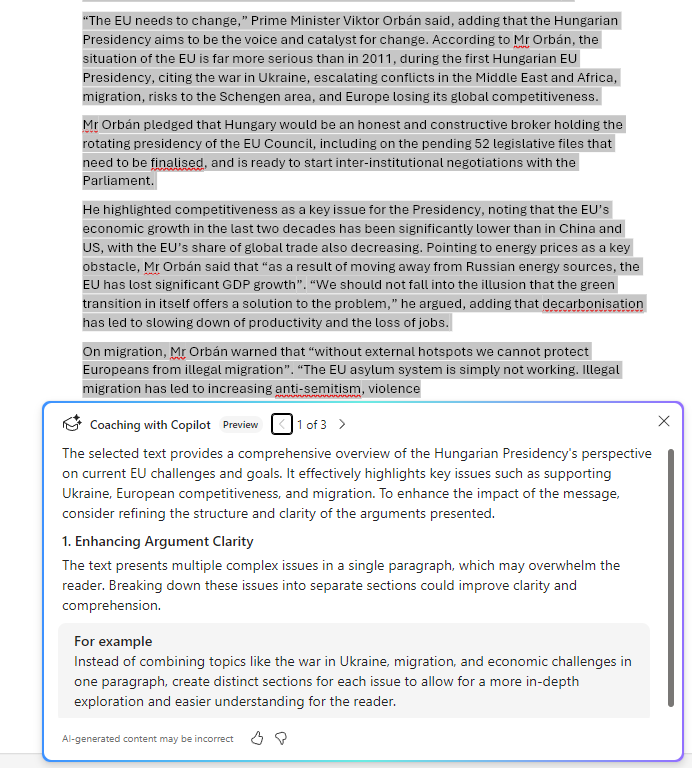
上图三种神经网络：标准、卷积（用于图像）、循环（序列化数据、时序数据）

数据类型：结构化（表格）、非结构化（语言、图片、文本）

二分类问题：

0、1判断问题，输入数据，判断是0或者1

逻辑回归：

• 输入数据x（可能是个n维向量），输出预测值。
• 表示标签（预测值）为1的概率
• 如果x是n维向量，约定逻辑回归参数w也是一个n维向量，参数b是实数。

线性回归的方法，但是在二分类问题上效果不好，因为我们想要得到的值是0或者1，但是线性回归得到的数值可能很大。

因此应用Sigmoid函数

逻辑回归的目标是学习参数w，b，使得更好估计输出标签为1的概率。

优化逻辑回归的代价函数：

通常使用平方错误来衡量Loss Function：

这个损失函数在逻辑回归中一般不用，因为当我们研究参数时，问题变成非凸问题，优化问题有多个局部最优解，梯度下降方法也无法找到全局最优解。

逻辑回归损失函数：（产生凸像最优问题）针对单个样本

全部训练数据集的Loss function总和的平均值即为训练集的代价函数（Cost function）

我们的目标是学习w,b使得代价函数最小，为了找到最优参数，往往是、初始化参数，对于逻辑回顾，几乎所有的初始化都是有效的，通常用0

梯度下降法：

参数更新

逻辑回归中如何计算导数实现梯度下降：

多个样本上的梯度下降：

代价函数的对于w的导数，可以看作每一个样本的导数和再平均