动态规划步骤:
- 状态表示。所谓状态表示就是 dp 表里的值表示什么含义,那么状态表示怎么找呢? a. 题目要求 b. 经验(以某一个位置为结尾 / 起点) + 题目要求 c. 分析问题的过程中发现重复子问题
- 状态转移方程。dp[ i ] 等于什么
- 初始化。保证填表的时候不越界
- 填表顺序。保证填写当前状态时,所需要的状态已经计算过了,初始化之后,下标的映射关系要一致
- 返回值。根据题目要求和状态表示进行返回
1. 不同路径
62. 不同路径

状态表示:以 dp[i][j] 为结尾,走到 dp[i][j] 位置时一共有几种方式
状态转移方程:
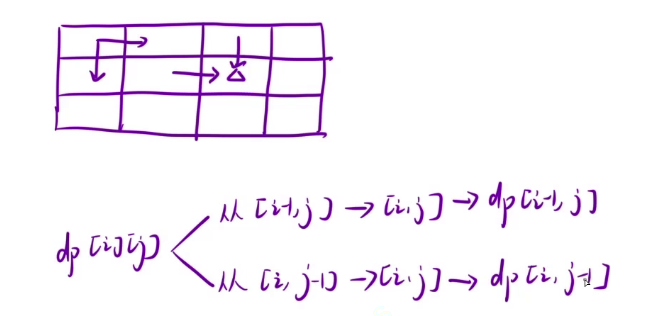
走到 (i , j) 位置时,它只可能是从上面的格子和左边的格子过来的,走到这两个格子之后再走一步就到 (i , j) 了,所以走到 (i, j) 位置的方式就是把走到上面的格子和左边的格子的方案数加起来,也就是 dp[i - 1][j] + dp[i][j - 1]
初始化:填 dp 表的时候,由于需要用到上边和左边的格子,填最上面的一行和最左边的一列时会越界,为了避免越界可以把 dp 表多开一列和一行,并且根据题目要求把这一行和一列赋上合适的值,以此确保能够正确的对 dp 表进行赋值
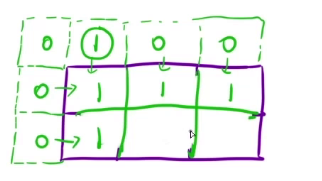
填表顺序:从上往下,从左到右
返回值:多开一行和一列之后返回的就是 dp[m][n],也就是要求的走到这个位置的方案数
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m + 1][n + 1];
dp[0][1] = 1;
for (int i = 1; i < dp.length; i++) {
for (int j = 1; j < dp[0].length; j++) {
dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
}
}
return dp[m][n];
}
}2. 不同路径 II
63. 不同路径 II

这题和上一题不同的就是加入了障碍物
状态表示:以 dp[i][j] 为结尾,走到 dp[i][j] 位置时一共有几种方式
状态转移方程:
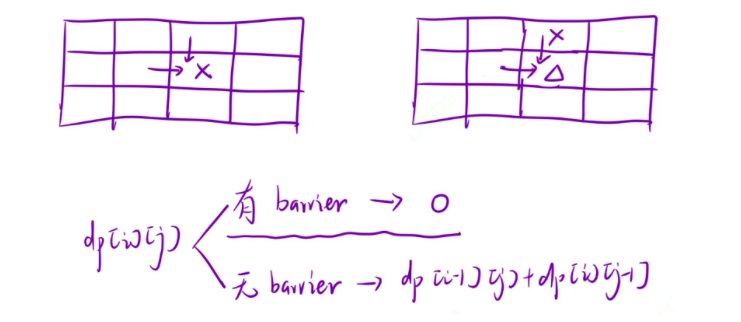
还是和上一道题一样,走到 (i , j) 位置时,它只可能是从上面的格子和左边的格子过来的,如果说有障碍物的时候,那么走到那个格子的方案数就是 0 ,如果 (i , j) 位置本身就是障碍物,也就是无论哪个格子都不能到达,dp[i][j] 也就是 0 ,其它情况正常相加即可
初始化:和上一题一样
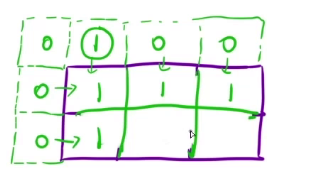
填表顺序和返回值都和上一题一样
下标的映射关系需要注意一下,由于这题在填 dp 表的时候需要判断当前位置是否是障碍物,所以需要通过遍历 arr 的下标进行填表,由于 dp 表多开了一行和一列,所以填表的时候下标都需要加一,或者是遍历 dp 表的下标,对 arr 进行减一
class Solution {
public int uniquePathsWithObstacles(int[][] arr) {
int[][] dp = new int[arr.length + 1][arr[0].length + 1];
dp[0][1] = 1;
for(int i = 0;i < arr.length;i++){
for(int j = 0;j < arr[0].length;j++){
if(arr[i][j] == 1){
dp[i+1][j + 1] = 0;
}else{
dp[i + 1][j + 1] = dp[i][j + 1] + dp[i + 1][j];
}
}
}
return dp[arr.length][arr[0].length];
}
}3. LCR 166. 珠宝的最高价值
LCR 166. 珠宝的最高价值

状态表示:到达 (i , j) 位置时可以获得珠宝的最大值
状态转移方程:其实和上面的题都非常类似,只能从上边的格子和左边的格子到达 (i , j) 位置,取这两个的最大值再加上 (i , j) 位置的价值即可
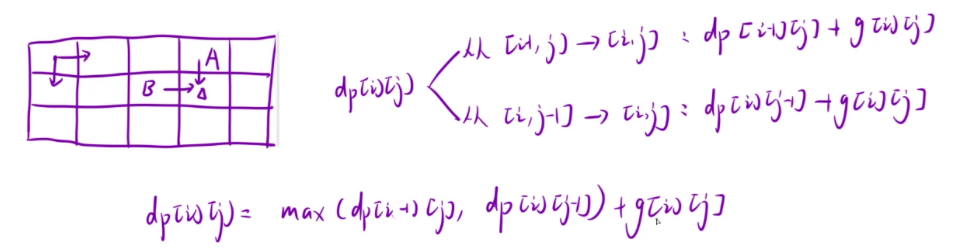
初始化:也和前面类似,为了不影响原来的值,把多开的一行和一列全设为 0 就行,同时也需要注意下标的映射关系
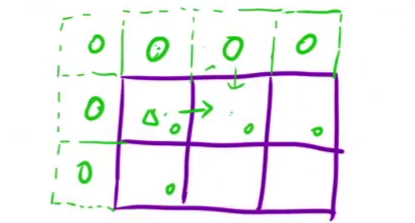
填表顺序:从上到下,从左到右
返回值:dp[m][n]
class Solution {
public int jewelleryValue(int[][] frame) {
int m = frame.length,n = frame[0].length;
int[][] dp = new int[m + 1][n + 1];
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
dp[i + 1][j + 1] = Math.max(dp[i][j + 1],dp[i + 1][j]) + frame[i][j];
}
}
return dp[m][n];
}
}4. 931. 下降路径最小和
931. 下降路径最小和

状态表示:dp[i][j] 表示到达 (i , j) 时的下降路径最小和
状态转移方程:(i , j) 位置只能由上面的位置和左上,右上的位置到达,求出三者的最小值再加上当前位置的值就是当前位置的路径最小和
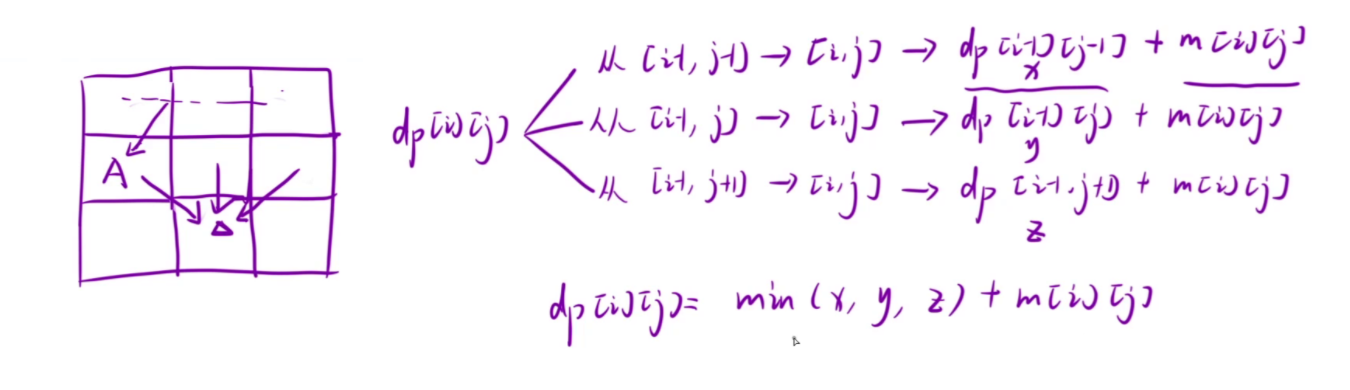
初始化:这次初始化所用到的数据就需要额外再多开一行和两列,
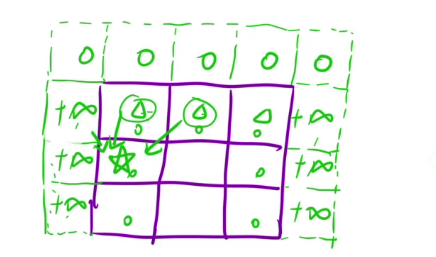
填表顺序:从上往下
返回值:最后一行的最小值
class Solution {
public int minFallingPathSum(int[][] matrix) {
int m = matrix.length,n = matrix[0].length + 1;
int[][] dp = new int[m + 1][n + 1];
for(int i = 1;i < m + 1;i++){
dp[i][0] = dp[i][n] = Integer.MAX_VALUE;
}
for(int i = 0;i < m;i++){
for(int j = 0;j < matrix[0].length;j++){
dp[i+1][j+1] = Math.min(Math.min(dp[i][j],dp[i][j + 1]),dp[i][j + 2]) + matrix[i][j];
}
}
int res = Integer.MAX_VALUE;
for(int i = 1;i < n;i++){
res = Math.min(res,dp[m][i]);
}
return res;
}
}5. 最小路径和
64. 最小路径和

这一题和珠宝最大和是非常相似的,不过就是这里要求最小的路径和
状态表示:dp[i][j] 表示到达 (i , j) 时的最小路径和
状态转移方程:
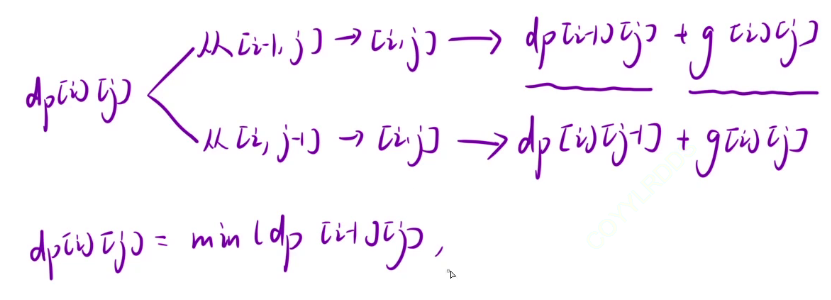
初始化:
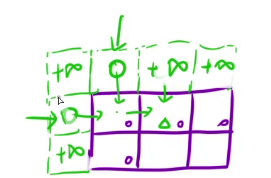
返回值:dp[m][n]
class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length,n = grid[0].length;
int[][] dp = new int[m + 1][n + 1];
for(int i = 0;i < m + 1;i++){
for(int j = 0;j < n + 1;j++){
dp[i][j] = Integer.MAX_VALUE;
}
}
dp[1][0] = dp[0][1] = 0;
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
dp[i+1][j + 1] = Math.min(dp[i + 1][j],dp[i][j+1]) + grid[i][j];
}
}
return dp[m][n];
}
}6. 地下城游戏
174. 地下城游戏
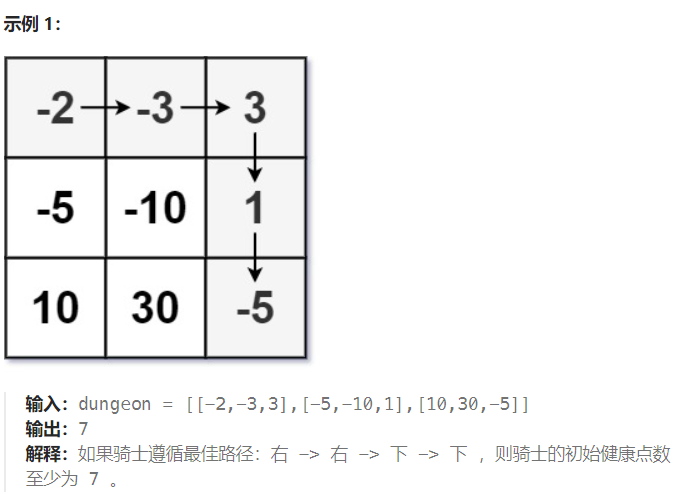
状态表示:根据之前的经验就是以 (i , j) 位置为结尾或者为开始
先来看以 (i , j) 位置为结尾的方式,此时就是从起点出发,到达 (i , j) 所需的最低初始健康点数,但是这个点的值还会受到右边和下边的影响的,如果说再走到右边或者下边就死了那这个健康点数就不对,所以这种方式退不出状态转移方程
接下来看另一种方式,以(i , j) 位置为开始到达终点所需的最低初始健康点数
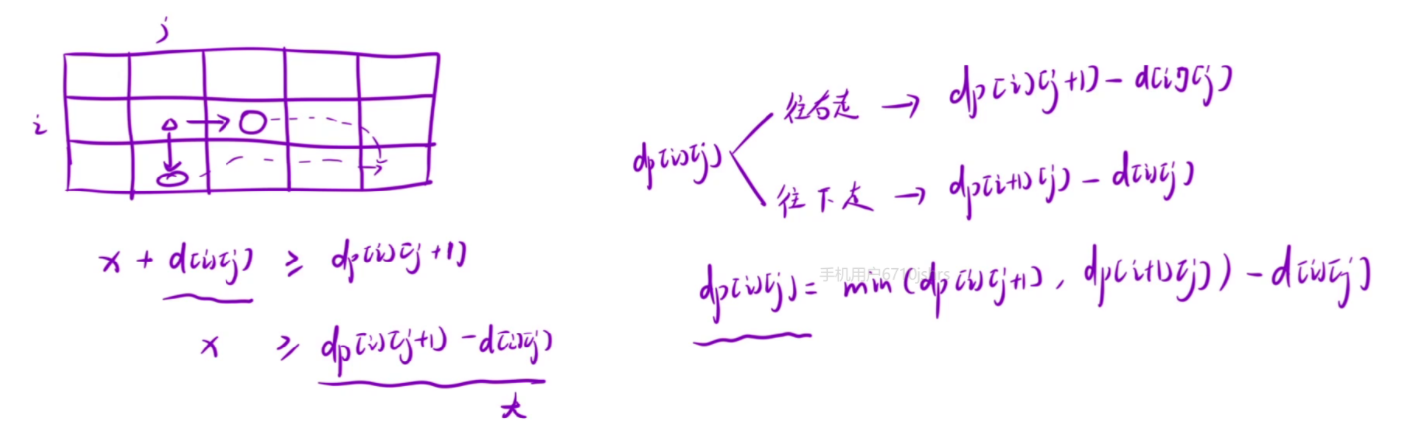
假设 dp[i][j] = x,如果说接下来可以走到右边或者下边,那么就需要令 x + dungeon[i][j] 的值大于右边或者下边的 dp 值,也就是从这个位置出去之后的血量需要大于下一步所需的最低健康点数,由于是最低,那么就不用是大于了,等于就可以了,接下来再求出是右边所需最低还是下边所需最低即可
但是结果可能会是一个负数,如果说当前位置回了一大口血,超过了下一步所需的最低血量,那么减出来的就是负数,也就是 dp[i][j] 是一个负数加上回的血 dungeon 就能通过,这是不合理的,所以当是负数的话就设置为 1
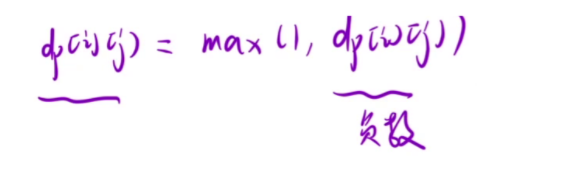
初始化:这次受到影响的是最后一行和最右边的一列
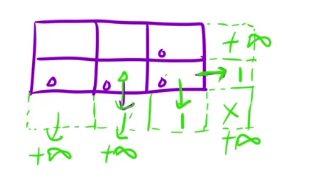
填表顺序:由于填 dp[i][j] 的时候需要用到右边和下边的值,所以需要先从右往左,再从下往上
返回值:返回 dp[0][0] 即可
class Solution {
public int calculateMinimumHP(int[][] dungeon) {
int m = dungeon.length, n = dungeon[0].length;
int[][] dp = new int[m + 1][n + 1];
for (int j = 0; j < dp[0].length; j++) {
dp[m][j] = Integer.MAX_VALUE;
}
for (int i = 0; i < dp.length; i++) {
dp[i][n] = Integer.MAX_VALUE;
}
dp[m][n - 1] = 1;
dp[m - 1][n] = 1;
for (int i = m - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
dp[i][j] = Math.min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];
dp[i][j] = Math.max(1, dp[i][j]);
}
}
return dp[0][0];
}
}