可以解决大部分区间上面的修改以及查询的问题，例如1.单点修改，单点查询，2.区间修改，单点查询，3.区间查询，区间修改，换言之，线段树能解决的问题，树状数组大部分也可以，但是并不一定都能解决，因为线段树的扩展性比树状数组要强.

先简单了解一下树状数组的结构有个大致印像

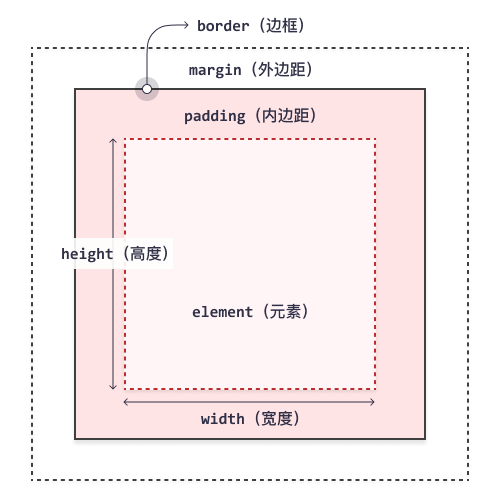
树状数组很像前缀和结合树形结构的实现方式，对于t[x]来说是一种变异的前缀和，它所表示的是[x-len + 1, x]这个范围的和，而len就是上图左侧的标注的对应值。（len的代表的什么又怎么求下面会详细描述）

根据上面解释的t[x]的含义，想必善于观察的同学已经发现了t[x]在图中的特点，我们可以举个栗子来归纳一下

根据连线关系可以得到如下关系:

t[4] = t[2] + t[3] + a[4]

t[6] = t[5] + a[6]

t[8] = t[4] + t[6] + t[7] + a[8]

t[3] = a[3]

t[5] = a[5]

t[7] = a[7]

是不是规律有点呼之欲出的感觉，我们发现：

• x为奇数时总等于a[x]

• x为2的倍数时t[x]就为它的所有子节点（t[]）加上a[x]的和。

所以我们想要快速求出t[x]就必须知道它有哪些子节点，这时候我们就需要引入一种特别的运算方法lowbit(x)，我们就是通过lowbit来求len的值

lowbit(x)的描述如下：求的是x的二进制表示下的最低位的1和此位后的0组成的值，如x = 4（100）时得到的就是100（4）；当x = 6(110)时得到的就是10（2）；x = 7(111)时得到的就是1（1）

而求解方法也很简单就是x&-x（x按位与上取反后的x），假如x=4, 因为最低位1后面都是0，所以取反后最低位1会变0，后面的0都会变1（0100 --> 1011 ），然后再+1就得到了-x（1100），接下来按位与：

    0100

& 1100

= 0100

就得到最后我们要的值。（不明白的可以先看看负数的二进制表示和按位与运算）

最后我们知道 len = lowbit(x){return x&-x;}

对于sum[7] = t[4] + t[6] + t[7]，而我们发现7-lowbit(7)=6，6-lowbit(6)=4，4-lowbit(4)=0，用x-lowbit(x)就能找到下一个需要的区间，同理x+lowbit(x)就能找到父节点。

到这里我们就可以总结一下t[x]的求法了

int lowbit(int x) {
	return x & -x;
}

//求和
int getSum(int x) {//往前找
	int sum = 0;
	for(int i = x; i > 0; i -= lowbit(i)){
		sum += t[i];
	}
	return sum;
}

//更新t[]
void update(int x, int val) {//往后找，找父节点
	for(int i = x; i<= bound ; i += lowbit(i)) {
		t[i] += val;
	}
}

void init() {
    int a[] = {0,2,3,4,1,6,4,7,8};//从下标为1开始
    for(int i = 1; i < a.length; i++) {
        update(i, x);
    }
}



//1.单点修改，单点查询
int main() {
	init();
    //单点修改
    update(x,y);//下标为x的值改变y;
    //单点查询  
    getSum(k);
}

//2.区间修改，单点查询
int main() {
	init();
    //区间修改  [m,n]改变y
    for(int i = m; i <= n; i++) {
        update(i, y);
    }
    //单点查询  
    getSum(k);
}

//3.区间查询，区间修改
自己动手尝试一下吧