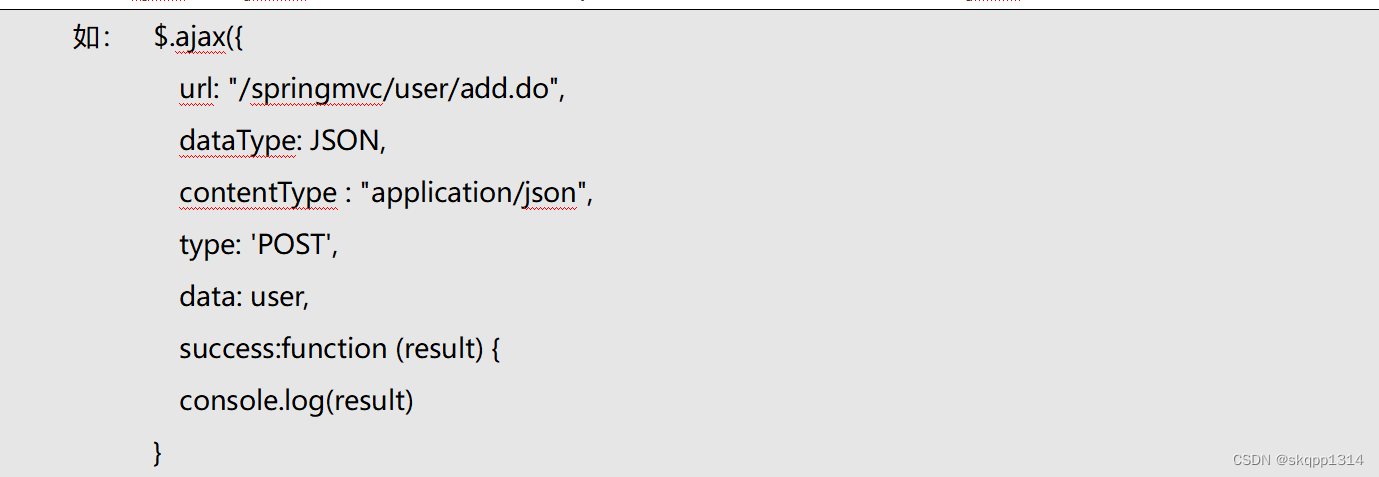
一.二叉树的存储
1.存储结构
存储结构:顺序存储或者是类似于链表的链式存储
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式
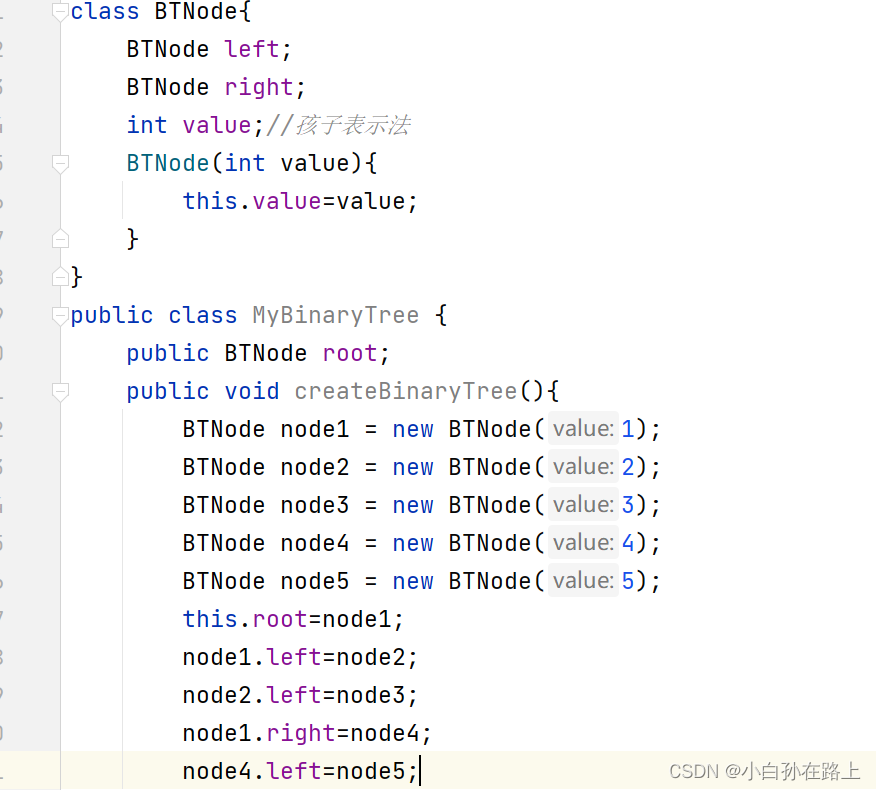
// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点2.创建一颗二叉树
二叉树是:
- 空树
- 非空:根节点,根节点的左子树、根节点的右子树组成

3.二叉树的性质
1.度为0的节点的个数比度为2 的节点个数多一个

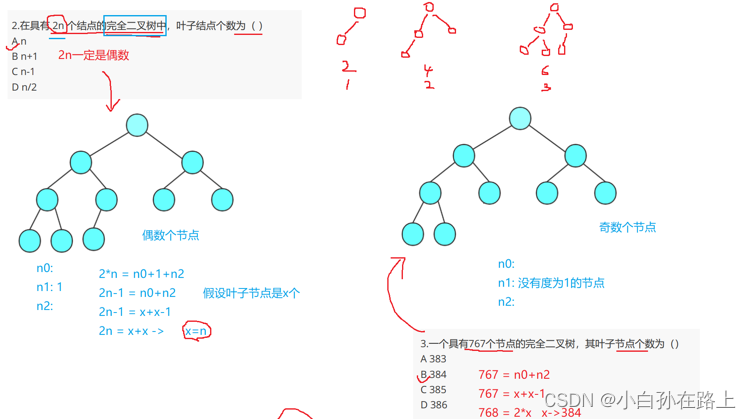
2.具有n个结点的完全二叉树的深度k为log2(n+1)上取整
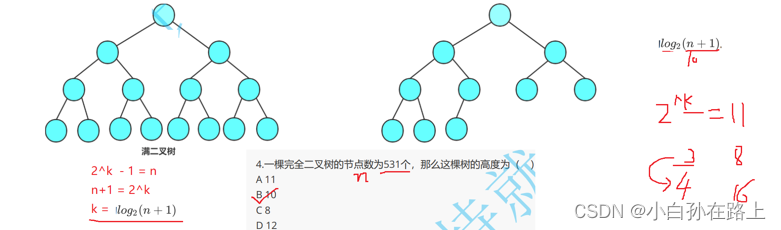
二的9次方为512.所以k一定是10/只是没有放满

二.二叉树的遍历
最简单的方式就是遍历。所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题(比如:打印节点内容、节点内容加1)。 遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算之基础。
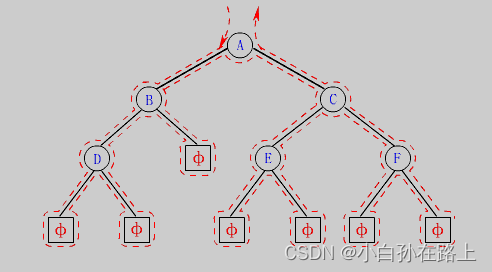
1. NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。
2. LNR:中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。
3. LRN:后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点。
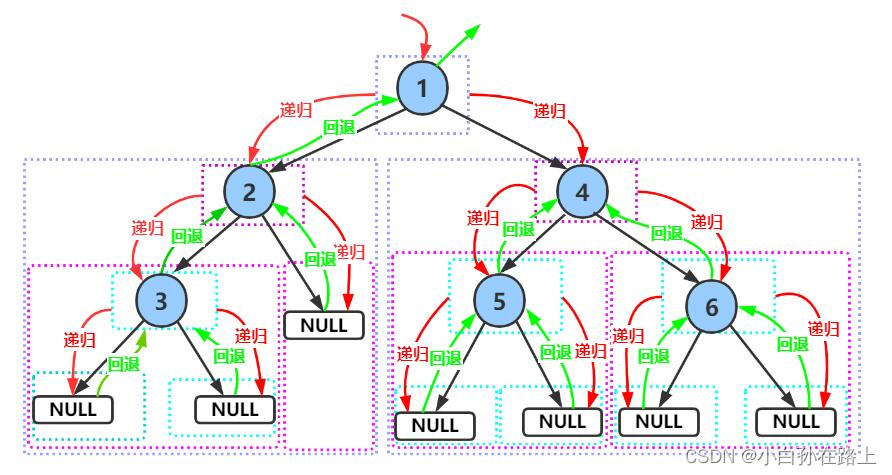
shift+F6可以把所有的更改 ctrl+r
4.层序遍历


1.子问题思路
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list=new ArrayList<>();
if(root==null){
return list;
}
list.add(root.val);
List<Integer> listleft= preorderTraversal(root.left);
list.addAll(listleft);
List<Integer> listright= preorderTraversal(root.right);
list.addAll(listright);
return list;
}
}2.遍历思路
class Solution {
List<Integer> list=new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {
if(root==null){
return list;
}
list.add(root.val);
preorderTraversal(root.left);
// list.add(root.val);
preorderTraversal(root.right);
// list.add(root.val);
return list;3.迭代思路
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list=new ArrayList<>();
Stack<TreeNode> stack=new Stack<>();
while(root!=null||!stack.isEmpty()){
while(root!=null){
list.add(root.val);
stack.add(root);
root=root.left;
}
root=stack.pop().right;
}
return list;
}
}将左边的值或者根节点放入栈中,依次弹出找右子树,如果右子树没有或者栈还有东西就还要继续往右边找,直到栈弹完剩下的或者找到新 的右子树.
三.二叉树有关习题
1.前n层和公示:2的n-1

2.排序二叉树
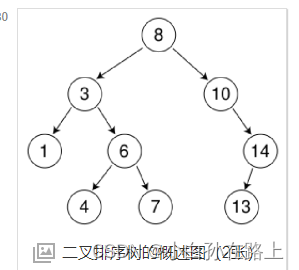

3.






![[附源码]计算机毕业设计JAVA基于JSP的美妆购买网站](https://img-blog.csdnimg.cn/e075b65117d14da698e27586ed4c5211.png)