OOOPS：零样本实现360度开放全景分割，已开源

全景图像捕捉360°的视场（FoV），包含了对场景理解至关重要的全向空间信息。然而，获取足够的训练用密集标注全景图不仅成本高昂，而且在封闭词汇设置下训练模型时也受到应用限制。为了解决这个问题，论文定义了一个新任务，称为开放全景分割（Open Panoramic Segmentation，OPS）。在该任务中，模型在源领域使用视场受限的针孔图像进行训练，而在目标领域使用视场开放的全景图像进行评估，从而实现模型的零样本开放全景语义分割能力。此外，论文提出了一种名为OOOPS的模型，结合了可变形适配器网络（Deformable Adapter Network，DAN），显著提高了零样本全景语义分割的性能。为了进一步增强从针孔源领域的失真感知建模能力，论文提出了一种新的数据增强方法，称为随机等矩形投影（Random Equirectangular Projection，RERP），该方法专门旨在预先处理物体变形。OOOPS模型结合RERP在OPS任务上超越了其他最先进的开放词汇语义分割方法，在三个人工全景数据集WildPASS、Stanford2D3D和Matterport3D上证明了其有效性，特别是在户外WildPASS上提升了+2.2%的性能，在室内Stanford2D3D上提升了+2.4%的mIoU。

来源：晓飞的算法工程笔记公众号，转载请注明出处

论文: Open Panoramic Segmentation

论文地址：https://arxiv.org/abs/2407.02685
论文代码：https://junweizheng93.github.io/publications/OPS/OPS.html

Introduction

全景成像系统在最近几年显著发展，这促进了多种全景视觉应用的产生。由于全面的360°视场，全天候全景图在感知周围环境时提供了更丰富的视觉线索，在广泛的场景理解任务中，使环境数据的捕获更加完整和沉浸，这对深入的场景理解至关重要。这种广角视角超越了针孔图像的有限范围，显著增强了计算机视觉系统在各种应用中感知和解析环境的能力。尽管与针孔图像相比，利用全景图像在计算机视觉应用中的好处显而易见，但必须不断考虑一些值得注意的挑战，具体如下：

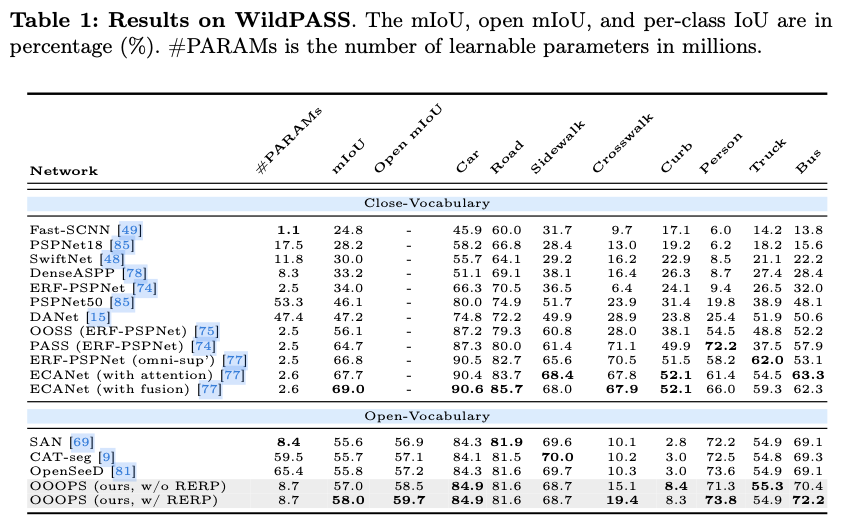
更广的视场挑战。例如，图1a展示了随着视场扩大，最先进的开放词汇语义分割方法的性能下降情况，即从针孔图像到360°全景图像。在这一过程中，观察到了超过 $12\%$ 的mIoU性能下降，表明了狭窄与宽广图像之间的语义和结构信息巨大差异所带来的挑战。
类别的限制。传统的封闭词汇分割任务范式仅提供有限数量的标注类别，这无法处理现实应用中不可估量的类别数量。图1b展示了封闭词汇分割与开放词汇分割之间的区别。与封闭词汇设置（第一行）相比，开放词汇设置（第二行）不受数据集类别数量的限制。在封闭词汇设置中，仅识别四个预定义的类别（以不同颜色突出），相对而言，开放设置中的每个全景像素都有其自有的语义意义，尽管数据集中没有对这些类别进行标注。

为了进一步释放全景图像的巨大潜力，有三个关键问题亟待解决：

如何通过单张图像获得整体感知？
如何突破现有全景数据集中有限可识别类别的障碍，以便下游视觉应用能够从无限制的信息视觉提示中受益？
如何应对全景标签的稀缺？

基于上述三个问题，论文提出了一项新任务，称为开放全景分割（Open Panoramic Segmentation，OPS），旨在全面解决这些挑战，更好地利用全景图像所带来的优势。新任务范式如图1c所示。开放全景分割任务考虑到三个问题的三个重要元素，“开放”的概念是三重的：全天候全景图像（开放视场），无限制的可识别类别范围（开放词汇）。此外，模型是在源域中使用针孔图像训练，而在目标域中评估使用全景图像（开放域）。考虑到密集标注的针孔分割标签与全景标签相比成本较低，因此开放不同领域是具有成本效益的。请注意，OPS与领域自适应（Domain Adaptation，DA）不同。在DA的训练背景下，数据的利用包括源域和目标域，而在OPS中，整个训练过程中完全依赖于仅来源于源域的数据。

除了新任务，论文提出了一种名为OOOPS的新模型，以应对OPS任务中提到的三个与开放性相关的挑战。该模型由一个冻结的CLIP模型和一个关键组件——可变形适配器网络（Deformable Adapter Network，DAN）组成，后者具有两个重要功能：(1) 高效地将冻结的CLIP模型适配到全景分割任务中，(2) 解决全景图像中的物体变形和图像失真。更具体而言，DAN的关键组件——新型可变形适配器操作符（Deformable Adapter Operator，DAO）旨在应对全景失真。为了提高模型对针孔源域失真感知的能力，论文进一步引入了随机等距投影（Random Equirectangular Projection，RERP），专门设计用来解决物体变形和图像失真。针孔图像被分割成四个图像块，并随机打乱。接着，在打乱后的图像中引入了等距投影，这是一种将球体映射到全景平面上的常用方法。OOOPS模型搭配RERP在WildPASS、Stanford2D3D和Matterport3D上分别超越了其他最先进的开放词汇分割方法，mIoU提高了+2.2% 、+2.4%和+0.6%。

总结来说，论文提出了以下贡献：

引入了一项新任务，称为开放全景分割（open panoramic segmentation，简称OPS），包括开放视场（Open FoV）、开放词汇（Open Vocabulary）和开放领域（Open Domain）。模型在源域中使用视场受限的针孔图像以开放词汇设置进行训练，而在目标域中使用视场开放的全景图像进行评估。
提出了一种名为OOOPS的模型，旨在同时解决三个与开放性相关的挑战。提出了一个可变形适配器网络（Deformable Adapter Network，DAN），用于将冻结的CLIP模型的零样本学习能力从针孔领域转移到不同的全景领域。
一种新颖的数据增强策略，称为随机等矩形投影（Random Equirectangular Projection，RERP），专门为所提出的OPS任务设计，进一步提高了OOOPS模型的准确性，在开放全景分割任务中实现了最先进的性能。
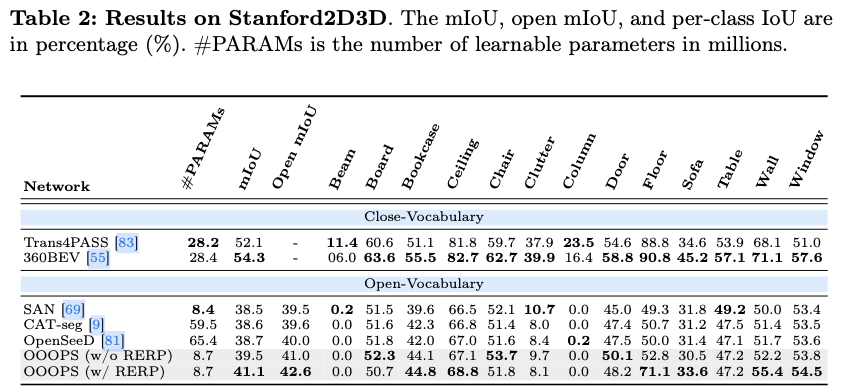
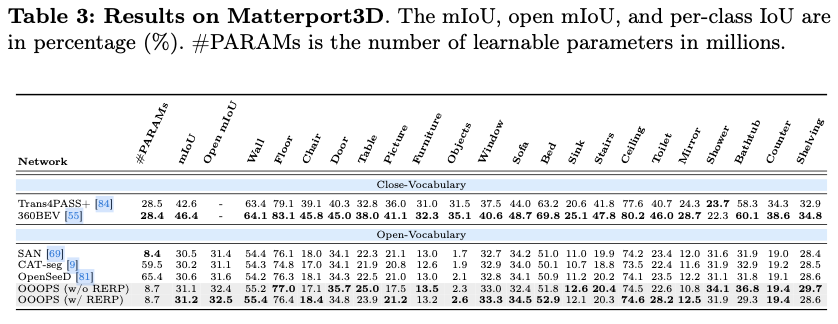
为了对OPS进行基准测试，在室内和室外数据集（WildPASS、Stanford2D3D和Matterport3D）上进行了全面评估，涉及超过10个近词汇和开放词汇的分割模型。

Methodology

Open Panoramic Segmentation

开放全景分割（OPS）任务旨在解决三个具有挑战性的问题：

狭窄的视场（FoV）
类别范围的限制
全景标签的匮乏

OPS对上述问题给出了三个解答：

开放视场
开放词汇
开放领域

OPS任务范式如图1c所示。模型在狭窄视场的针孔源领域中以开放词汇的设置进行训练，而在宽视场的全景目标领域中进行评估。

Model Architecture

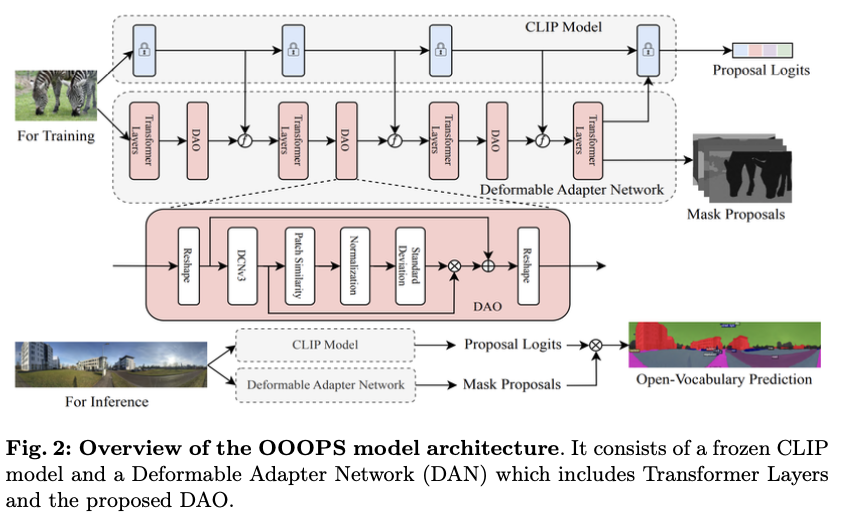
基础模型可以通过使用适配器高效地转移到下游任务。为了提高全景建模能力，论文设计了OOOPS模型。如图2所示，它由一个冻结的CLIP模型和一个提出的可变形适配器网络（DAN）组成，后者结合了多个变换层和新颖的DAO。特征融合发生在CLIP和DAN的中间层之间。DAN的两个输出之一包含掩膜提议，而另一个则作为深度监督指导，帮助CLIP生成提议的logits。

在训练阶段，针孔图像被输入到OOOPS中，生成掩膜提议和用于损失计算的提议logits。在推理阶段，全景图像被输入到OOOPS中，通过掩膜提议与相应提议logits的乘积生成分割预测。冻结的CLIP对于OOOPS的零样本学习能力是必要的。

Deformable Adapter Network

可变形适配器网络是多个变换层与提出的DAO的结合。由于全景图像中存在失真，这在利用信息丰富的全景图像时是一个巨大的挑战。论文深入探讨了可变形设计和采样方法，如APES和MateRobot，提出了DAO以应对全景图像的失真和物体变形。

Revisiting DCN Series

开创性工作DCN可以赋予传统CNN空间变形感知的能力。给定一个具有 $K$ 个采样位置的卷积核，设 $\mathbf{w}_k$ 和 $\mathbf{p}_k$ 分别表示第 $k$ 个位置的权重和预设偏移。例如， $K{=}9$ 且 $\mathbf{p}_k {\in} \{(1,1), \ldots, (-1,-1)\}$ 定义了一个膨胀率为 $1$ 的 $3{\times}3$ 卷积核。让 $\mathbf{x}(\mathbf{p})$ 和 $\mathbf{y}(\mathbf{p})$ 分别表示输入特征图 $\mathbf{x}$ 和输出特征图 $\mathbf{y}$ 在位置 $\mathbf{p}$ 的特征。DCN的公式化为：

$\begin{equation} \mathbf{y}(\mathbf{p}) = \sum^K_{k=1}\mathbf{w}_k\mathbf{x}(\mathbf{p}+\mathbf{p}_k+\Delta\mathbf{p}_k), \end{equation}$

其中 $\Delta\mathbf{p}_k$ 是第 $k$ 个位置的可学习偏移。尽管DCN能够捕捉空间变形，但在计算局部特征时，每个采样位置被视为相同。DCNv2的提出增加了一个称为调制标量的附加项。具体而言，DCNv2可以表示为：

$\begin{equation} \mathbf{y}(\mathbf{p}) = \sum^K_{k=1}\mathbf{w}_k\mathbf{m}_k\mathbf{x}(\mathbf{p}+\mathbf{p}_k+\Delta\mathbf{p}_k), \end{equation}$

其中 $\mathbf{m}_k$ 是第 $k$ 个位置的可学习调制标量。受Transformer的启发，DCNv3提出了一种分组操作，进一步增强了DCNv2的变形感知能力。DCNv3可以用以下公式表示：

$\begin{equation} \mathbf{y}(\mathbf{p}) = \sum^G_{g=1}\sum^K_{k=1}\mathbf{w}_g\mathbf{m}_{gk}\mathbf{x}_g(\mathbf{p}+\mathbf{p}_k+\Delta\mathbf{p}_{gk}), \end{equation}$

其中 $G$ 表示聚合组的总数。DCNv4与DCNv3类似，能够实现相似的性能，同时显著减少运行时间。

Deformable Adapter Operator (DAO)

在处理全景图中的畸变时，DCNv3和DCNv4未能满足变形感知的要求。因此，提出了DAO来利用以下表达式解决全景图像中的畸变问题：

$\begin{equation} \mathbf{y}(\mathbf{p}) = \mathbf{s}(\mathbf{p})\sum^G_{g=1}\sum^K_{k=1}\mathbf{w}_g\mathbf{m}_{gk}\mathbf{x}_g(\mathbf{p}+\mathbf{p}_k+\Delta\mathbf{p}_{gk}), \end{equation}$

其中 $\mathbf{s(\mathbf{p}})$ 是位置 $\mathbf{p}$ 处的可学习显著标量。DAO继承自DCNv3，提出了一个额外的项，称为显著标量，以指示全景图中每个像素的重要性。值得注意的是，DCNv3和DCNv4共享相同的数学表达式，但根据设计DAO之前的实验，DCNv3更为稳健。因此，论文选择将DCNv3作为DAO的一部分，而不是DCNv4。

如图2所示，通过DCNv3输出的特征图依次经过Patch相似性层、归一化层和标准差层，以形成显著图。这种设计的直觉是简单明了的：图像中的显著像素是那些与其邻近像素有显著区别的像素，例如边缘像素。如果一个图像块中的所有像素都不同，则该块内像素相似性的标准差将高于包含相似像素的块，从而导致更高的显著标量。

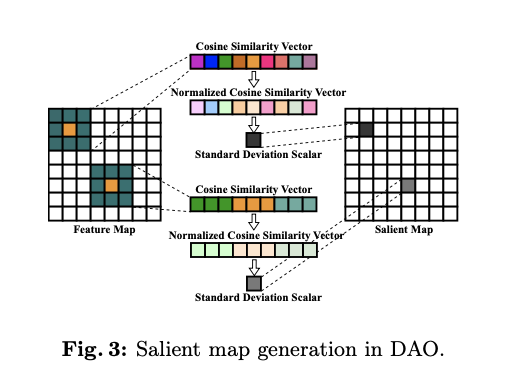
图3更详细地解释了显著图的生成过程。给定一个特征图，DAO首先计算中心像素与卷积核内所有像素之间的余弦相似度，例如，图3中的 $\times 3$ 卷积核内的 $9$ 个像素，结果是一个 $9$ 维的余弦相似度向量。然后对该向量应用Softmax归一化。随后，DAO计算这个归一化余弦相似度向量的标准差，以指示中心像素的重要性。通过遍历整个特征图中的每个像素，生成一个显著图，以增强通常是图像边缘像素的显著性，在这些位置常常会发生强烈的全景畸变。

Random Equirectangular Projection

等距矩形投影（ERP）是将球体映射到全景平面最常见的方法之一，它将球面坐标转换为平面坐标，如下所示：

$\begin{align} &x = R(\lambda-\lambda_0)cos(\varphi_1), \\ &y = R(\varphi-\varphi_0), \end{align}$

其中 $\lambda$ 和 $\varphi$ 分别是要投影位置的经度和纬度。 $\varphi_1$ 是标准纬线。 $\lambda_0$ 和 $\varphi_0$ 分别是地图的中央子午线和中央纬线。 $R$ 是球体的半径。 $x$ 表示投影位置在地图上的水平坐标， $y$ 表示垂直坐标。

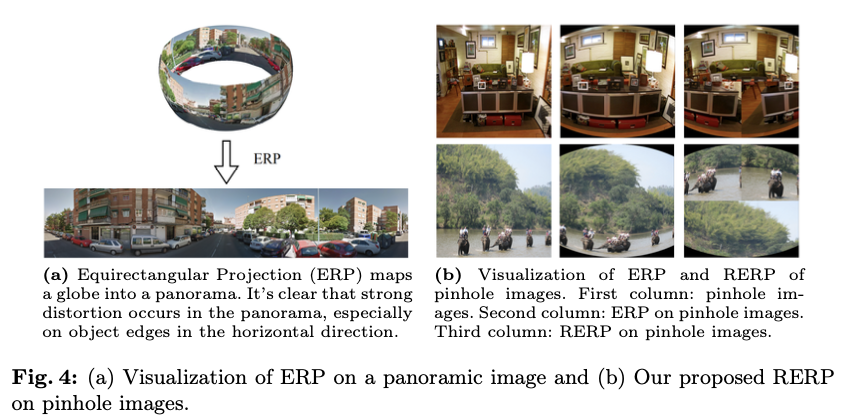
图4a可视化了全景平面上的等距矩形投影。可以观察到，在等距矩形投影后，全景图中出现了强烈的畸变，例如，直线被转换为曲线。为了进一步提高性能，论文在针孔图像上提出了随机等距矩形投影（RERP），因为OPS任务要求模型使用针孔图像进行训练，而不是全景图像。

将针孔图像分成四部分，并随机打乱图像块,随后对无畸变的针孔图像应用等距矩形投影。图4b可视化了经过随机等距矩形投影（RERP）后的针孔图像。第一列是未进行任何数据增强的针孔图像。第二列是未进行随机打乱的针孔图像上的等距矩形投影（ERP）。最后一列是论文提出的随机等距矩形投影（RERP）。可以观察到，在经过RERP后的针孔图像中也出现了类似全景的畸变。随机打乱用于增强鲁棒性并促进泛化。