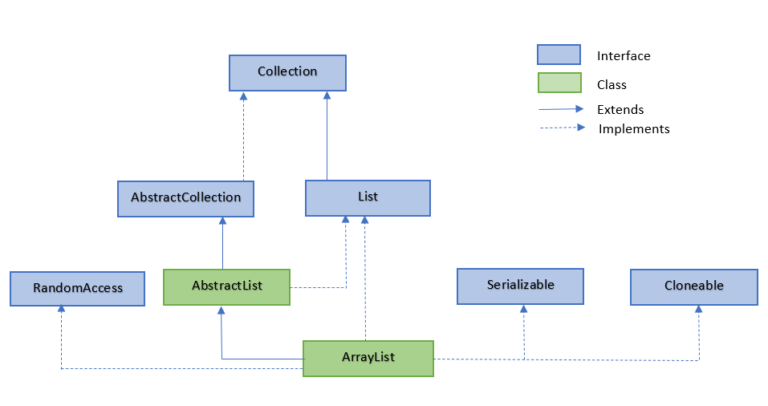
首先区分概念

“度为m的树”指的是至少有一个结点的度是m，一定是非空树

“m叉树”指的是允许所有的结点都小于m，且可以是空树

常见考点：

度为m的树的第i层最多有个结点  （对于m叉树也相同）

第一层m的0次方

第二层m的1次方

第三层m的2次方

第四层m的3次方

 高度为h的m叉树最多有个结点

 对于高度为h的m叉树至少有h个结点（每层只有一个结点）

对于高度为h的度为m的树至少有h+m-1个结点

 对于具有n个结点的m叉树的最小高度为

不用死记硬背：推导即可

 

---

二叉树

可能存在的五种形态：空二叉树、只有左子树（右子树为空）、只有右子树（左子树为空）、只有根节点、左右子树都有

满二叉树：一颗高度为h，且具有个结点的二叉树

·只有最后一层有叶子结点

·不存在度为1 的结点

·从根节点开始从1编号，结点i的父节点为[i/2]

完全二叉树是一种特殊类型的二叉树，其中树的所有级别都被完全填充，除了最低级别的节点从尽可能左侧填充之外。

另外可以理解为：遍历一个完全二叉树的所有结点都能在满二叉树中找到一一对应的结点，满二叉树一定是完全二叉树，但是完全二叉树不一定是满二叉树

·只有最后两层有叶子节点

·最多只有一个度为1的结点

·从根节点开始从1编号，结点i的父节点为[i/2]

·i<=[n/2]为分支结点，i>[n/2]为叶子结点  ,其中n为最大的结点数

·如果某一个结点只有一个子节点，那么其一定是左子节点

二叉排序树。左子树上的所有结点关键字都小于根节点的关键字

右子树上的所有结点的关键字都大于根节点的关键字

同时左子树和右子树又各是一颗二叉排序树

平衡二叉树。树上的任一结点的左子树和右子树的深度之差不超过1

如果一个二叉排序树是一个平衡二叉树，则其搜索效率要高很多

二叉树考点

1、设非空二叉树中度为0、1和2的结点个数分别为n0、n1和n2，如n0=n2+1(叶子结点的个数要比二分支结点的个数多1个)

2、二叉树的第i层最多有个结点

3、高度为h的二叉树最多有个结点

4、具有n个结点的完全二叉树的高度h为

5、对于一个完全二叉树，给出了结点n的个数，可以直接推算出度为0\1\2的结点个数n0\n1\n2

        推到过程： 完全二叉树最多只会有一个度为1的结点，即n1=0或1

                        n0 = n2 +1,则叶子结点和双分支结点（度为2的结点）的总和、差都是奇数

                        如果一个完全二叉树给出的总结点个数是偶数个（2k），则n0=k,n1=1,n2=k-1

                        如果一个完全二叉树给出的总结点个数是奇数个（2k-1），则n0=k,n1=0,n2=k-1

对于一个完全二叉树，给定总结点的个数num，则n0= num/2 , n2 = n0-1  ,如果num是偶数，则n1= 1 , 如果Num是奇数， 则n1 = 0;

 6、对于顺序存储的二叉树的结点i ,其

左子结点：2i

右子结点：2i+1 

父节点: [i/2]

i所在的高度h : log2(n+1)

 对于完全二叉树，总结点数n:

判断i是否有左子节点：2i<=n?

判断i是否有右子节点：2i+1<=n?

判断是否是叶子结点还是分支结点： i 与[n/2]对比

对于完全二叉树，要有结点数与分支结点数对半分割的思想：

---

二叉树遍历方式：

先序遍历：根-左-右： A-BDE-CFG

中序遍历：左-根-右：DBE-A-FCG

后序遍历：左-右-根：DEB-FGC-A

 

先序遍历：根-左-右：A-BDGE-CF

中序遍历：左-根-右：DGBE-A-FC   (G是右节点)

后序遍历：左-右-根：GDEB-FC-A

求取数的深度：

int treeDepth (BiTree T){
    if(T==NULL){
        return 0;
    }
}
    else {
        int l = treeDepth(T->lchild)
        int r = treeDepth(T->rchild)
        return l>r ? l+1 :r+1;
}

层序遍历：

思想：初始化一个队列queue,让根节点入队，如果队列Q非空，则pop一个元素并读取访问，将其指向的左子节点和右子节点插入队列，然后重复上述

struct TreeNode{
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x),left(NULL),right(NULL){}
}
void levelOrder(TreeNode* root)
{
    if(root ==NULL ) return ;
    queue<TreeNode*> q;
    q.push(root);
    while(!q.empty())
    {
        TreeNode* cur = q.front();
        q.pop();
        
        //输出当前结点的值
        cout <<cur ->val <<endl;        
    
        if(cur->left !=NULL){
            q.push(cur->left);
        }
        if(cur->right!=NULL)    
        {
            q.push(cur->right);
        }
    }
}