咱们来聊聊,啥样的预测模型才算是好模型?简单来说,就是那种在处理它从没见过的数据时,也能表现得特别棒的模型。老派的泛化理论告诉我们,要想让模型在训练集和测试集上都表现差不多,就得让模型简单点。这个简单,可以是参数少一点,还可以权重衰减,其实就是让参数的值别太大,这也是让模型保持简单性的一个好方法。还有一个概念就是平滑性,意思是说,模型对输入数据的小变化应该不那么敏感。比如在图像分类任务中,我们希望即使图像上有点随机噪声,模型也能正确地识别出来。
时间快进到1995年,有个叫克里斯托弗·毕晓普的大佬,他把这种想法变成了数学上的理论。他证明了,如果在训练时给输入数据加上点噪声,这实际上就相当于做了Tikhonov正则化。他的工作把函数需要平滑(也就是简单)的要求,和对输入扰动的抵抗力,这两者之间的数学关系给说清楚了。
然后到了2014年,Srivastava他们想出了一个绝妙的点子,就是怎么把毕晓普的想法用到神经网络的内部层。他们建议在训练的时候,在计算下一层之前,给网络的每一层都注入点噪声。他们发现,这样做可以让深层神经网络的输入输出映射更加平滑。
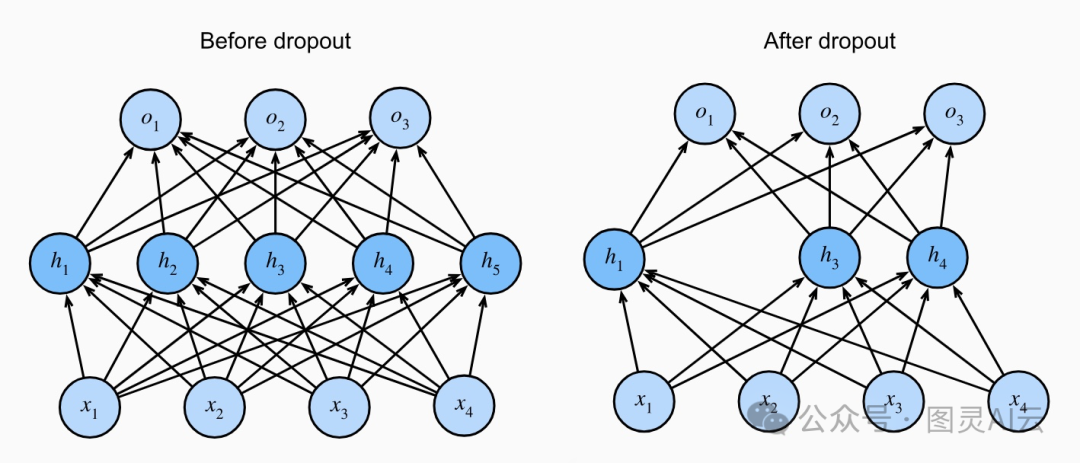
他们提出的这个点子,叫做Dropout,现在已经成了训练神经网络的标准操作了。这个操作之所以叫dropout,是因为在训练过程中,我们真的会“丢掉”一些神经元。每次迭代的时候,我们会随机把一些节点的输出置为零,这样下一层的计算就不会用到这些节点了。
直白一些,Dropout是深度神经网络里用来防止模型太复杂、记性太好的一种技巧。就像是,我们故意让网络忘记一些东西,这样它就不会把所有的训练数据都记得太死,从而在遇到新数据时能更好地适应。
简单来说,神经网络就像是一堆小团队,每个团队都忙着处理信息。但是,如果每个团队都只关注自己的工作,不跟别人合作,那整个网络处理信息的能力就会受到影响。所以,dropout就是在训练的时候,随机让一些团队暂时离线,这样剩下的团队就得学会在缺少某些信息的情况下工作。
为啥这么做呢?因为我们不想让模型只在训练数据上表现好,而是真的想让它在现实世界中也能派上用场。如果模型对训练数据记得太清楚,它可能就会忽略掉那些它没见过的新信息,这就是所谓的过拟合。Dropout就是通过让网络“忘记”一些信息,来防止这种情况发生的。
Dropout层的意思就是,在神经网络中故意忽略掉一些信息,好让模型不会过于依赖某些特定的数据点。
就好比我们的大脑,随时都在处理一大堆乱七八糟的信息,但不是所有的信息都是重要的。神经网络也是这样,它的每个单元都在忙忙碌碌地接收和发送信息,但这些信息里头,有的是关键的,有的可能就是干扰项。
数据科学家们用dropout这个技巧,就是想在模型学习的过程中,随机地让一些单元不工作,这样就能减少那些干扰项的影响。具体操作起来,他们会在神经网络的不同层用不同的策略来应用dropout:
-
输入层:这就像是神经网络的大门,原始数据就是从这儿进来的。如果有些数据跟我们要解决的问题没啥关系,就可以在这儿用dropout忽略掉。
-
中间层或隐藏层:这些层就像是神经网络的加工车间,数据进来后在这里经过一系列的处理。但是,这些处理的结果并不都是最终答案,很多都只是半成品。因为这些半成品里头可能包含了不少噪声,所以数据科学家们会在这些层用dropout来减少噪声。
-
输出层:这是神经网络给出最终答案的地方,这里的信息都是最重要的,所以通常不会用dropout。
总的来说,dropout就是数据科学家们用来提高模型泛化能力,避免过拟合的一种手段。通过dropout,可以让模型更加专注于学习那些真正重要的信息。
Dropout的实际例子和用场挺多的,我给你举两个例子来说明它是咋回事:
-
太空信号监听:想象一下,有个组织专门监控从宇宙深处传来的声音,他们想找的是那些重复的、有规律的信号,因为这可能意味着外星生命的存在。他们把收集到的声音信号送到神经网络里进行分析。在分析前,科学家们会先筛掉那些听起来乱七八糟、没啥规律的声音。同时,他们还会在神经网络的中间处理环节,故意忽略掉一部分数据,这样可以减少计算量,加快找出结果的速度。
-
生化公司研发新材料:再比如,有一家生化公司想研发一种全新的塑料。他们已经知道需要哪些基本元素来组成这种塑料,但具体的配方还不知道。为了节省研究时间和计算资源,他们用了一个神经网络来筛选全球的相关研究资料,但这个网络只关注那些直接和这种分子及其元素有关的研究,其他不相关的信息都会被自动过滤掉。这样做的好处是,他们的AI模型就不会出现过拟合,也就是不会因为数据太杂太乱而做出错误的预测。
最后来聊聊大型语言模型里怎么用dropout来帮忙模型学得更好?
首先,咱们得决定在哪里加dropout。通常是在词嵌入完了之后、每个处理层(比如Transformer或RNN)之后,有时候甚至在输出前也会加一点。
接下来,得挑个合适的dropout率,这个得靠试。一般这个率在0.1到0.5之间,每层可能还不一样,有时候中间那些层可能需要更大一点。
然后,得多做实验,用交叉验证来看看不同的dropout率哪个最好。这个过程可以用些自动化的工具来帮忙。
训练的时候,每次都得随机让一些神经元不工作,但测试的时候就全用上,这样模型就能好好表现了。
如果是特别大的模型,可能得多用点dropout,因为大模型容易记住太多东西,不太容易适应新情况。
dropout还可以和其他方法一起用,比如让权重小一点或者用更多的数据,这样模型能更好地适应各种情况。
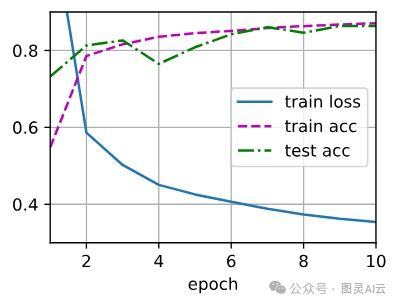
训练的时候得看着点,比如损失是不是小了,准确率是不是高了,这些都是dropout有没有用的信号。
还可以用些工具来搞清楚dropout到底是咋帮忙的。
最后,训练和测试的时候dropout得保持一致,别一会儿用一会儿不用的。
用dropout就是为了让模型别太死记硬背,碰到新情况也能应对。这个得好好调调,确保它真能帮上忙,但又不会让模型学得太差。
接下来,我们分别用mxnet,pytorch 及 tensorflow 来简单以代码的方式来从头开始实现一下,注意不保证代码的完整性,只做参考。
要实现单层的dropout函数,我们必须根据层的维度从伯努利(二元)随机变量中抽取尽可能多的样本,其中随机变量以概率(1-p)取值(1)(保留)和概率(p)取值(0)(丢弃)。一种简单的实现方法是首先从均匀分布(U[0, 1])中抽取样本。然后我们可以保留对应样本大于(p)的节点,丢弃其余的。
在下面的代码中,我们实现了一个dropout_layer函数,它以概率dropout丢弃张量输入X中的元素,然后按照上述描述重新缩放剩余部分:将幸存者除以1.0-dropout。
from mxnet import autograd, gluon, init, np, npx
from mxnet.gluon import nn
from d2l import mxnet as d2l
npx.set_np()
def dropout_layer(X, dropout):
assert 0 <= dropout <= 1
# 在这种情况下,所有元素都被丢弃
if dropout == 1:
return np.zeros_like(X)
# 在这种情况下,所有元素都被保留
if dropout == 0:
return X
mask = np.random.uniform(0, 1, X.shape) > dropout
return mask.astype(np.float32) * X / (1.0 - dropout)
import torch
from torch import nn
from d2l import torch as d2l
def dropout_layer(X, dropout):
assert 0 <= dropout <= 1
# 在这种情况下,所有元素都被丢弃
if dropout == 1:
return torch.zeros_like(X)
# 在这种情况下,所有元素都被保留
if dropout == 0:
return X
mask = (torch.rand(X.shape) > dropout).float()
return mask * X / (1.0 - dropout)
import tensorflow as tf
from d2l import tensorflow as d2l
def dropout_layer(X, dropout):
assert 0 <= dropout <= 1
# 在这种情况下,所有元素都被丢弃
if dropout == 1:
return tf.zeros_like(X)
# 在这种情况下,所有元素都被保留
if dropout == 0:
return X
mask = tf.random.uniform(
shape=tf.shape(X), minval=0, maxval=1) < 1 - dropout
return tf.cast(mask, dtype=tf.float32) * X / (1.0 - dropout)
我们可以在一些示例上测试dropout_layer函数。在下面的代码行中,我们以概率0、0.5和1通过dropout操作传递我们的输入X。
X = np.arange(16).reshape(2, 8)
print(dropout_layer(X, 0))
print(dropout_layer(X, 0.5))
print(dropout_layer(X, 1))
X= torch.arange(16, dtype = torch.float32).reshape((2, 8))
print(X)
print(dropout_layer(X, 0.))
print(dropout_layer(X, 0.5))
print(dropout_layer(X, 1.))
X = tf.reshape(tf.range(16, dtype=tf.float32), (2, 8))
print(X)
print(dropout_layer(X, 0.))
print(dropout_layer(X, 0.5))
print(dropout_layer(X, 1.))
接下来,定义模型参数,我们可以使用Fashion-MNIST数据集。下面定义了一个具有两个隐藏层,每个隐藏层包含256个单元的MLP。
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
W1 = np.random.normal(scale=0.01, size=(num_inputs, num_hiddens1))
b1 = np.zeros(num_hiddens1)
W2 = np.random.normal(scale=0.01, size=(num_hiddens1, num_hiddens2))
b2 = np.zeros(num_hiddens2)
W3 = np.random.normal(scale=0.01, size=(num_hiddens2, num_outputs))
b3 = np.zeros(num_outputs)
params = [W1, b1, W2, b2, W3, b3]
for param in params:
param.attach_grad()
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
num_outputs, num_hiddens1, num_hiddens2 = 10, 256, 256
这个时候,可以定义模型了。
下面的模型在每个隐藏层的输出(激活函数之后)应用dropout。我们可以为每层分别设置dropout概率。一个常见的趋势是在接近输入层的地方设置较低的dropout概率。下面我们将第一层和第二层的dropout概率分别设置为0.2和0.5。我们确保dropout只在训练期间激活。
dropout1, dropout2 = 0.2, 0.5
def net(X):
X = X.reshape(-1, num_inputs)
H1 = npx.relu(np.dot(X, W1) + b1)
# 仅在训练模型时使用dropout
if autograd.is_training():
# 在第一个全连接层之后添加一个dropout层
H1 = dropout_layer(H1, dropout1)
H2 = npx.relu(np.dot(H1, W2) + b2)
if autograd.is_training():
# 在第二个全连接层之后添加一个dropout层
H2 = dropout_layer(H2, dropout2)
return np.dot(H2, W3) + b3
dropout1, dropout2 = 0.2, 0.5
class Net(nn.Module):
def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,
is_training = True):
super(Net, self).__init__()
self.num_inputs = num_inputs
self.training = is_training
self.lin1 = nn.Linear(num_inputs, num_hiddens1)
self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
self.lin3 = nn.Linear(num_hiddens2, num_outputs)
self.relu = nn.ReLU()
def forward(self, X):
H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
# 仅在训练模型时使用dropout
if self.training == True:
# 在第一个全连接层之后添加一个dropout层
H1 = dropout_layer(H1, dropout1)
H2 = self.relu(self.lin2(H1))
if self.training == True:
# 在第二个全连接层之后添加一个dropout层
H2 = dropout_layer(H2, dropout2)
out = self.lin3(H2)
return out
net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)
dropout1, dropout2 = 0.2, 0.5
class Net(tf.keras.Model):
def __init__(self, num_outputs, num_hiddens1, num_hiddens2):
super().__init__()
self.input_layer = tf.keras.layers.Flatten()
self.hidden1 = tf.keras.layers.Dense(num_hiddens1, activation='relu')
self.hidden2 = tf.keras.layers.Dense(num_hiddens2, activation='relu')
self.output_layer = tf.keras.layers.Dense(num_outputs)
def call(self, inputs, training=None):
x = self.input_layer(inputs)
x = self.hidden1(x)
if training:
x = dropout_layer(x, dropout1)
x = self.hidden2(x)
if training:
x = dropout_layer(x, dropout2)
x = self.output_layer(x)
return x
net = Net(num_outputs, num_hiddens1, num_hiddens2)
最后,进行训练和测试。
num_epochs, lr, batch_size = 10, 0.5, 256
loss = gluon.loss.SoftmaxCrossEntropyLoss()
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs,
lambda batch_size: d2l.sgd(params, lr, batch_size))
num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
num_epochs, lr, batch_size = 10, 0.5, 256
loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = tf.keras.optimizers.SGD(learning_rate=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)