原来机器学习这么简单—

原来机器学习这么简单——线性回归

news2024/10/9 17:41:49

引言：
在正文开始之前，首先给大家介绍一个不错的人工智能学习教程：https://www.captainbed.cn/bbs。其中包含了机器学习、深度学习、强化学习等系列教程，感兴趣的读者可以自行查阅。

一、什么是线性回归？

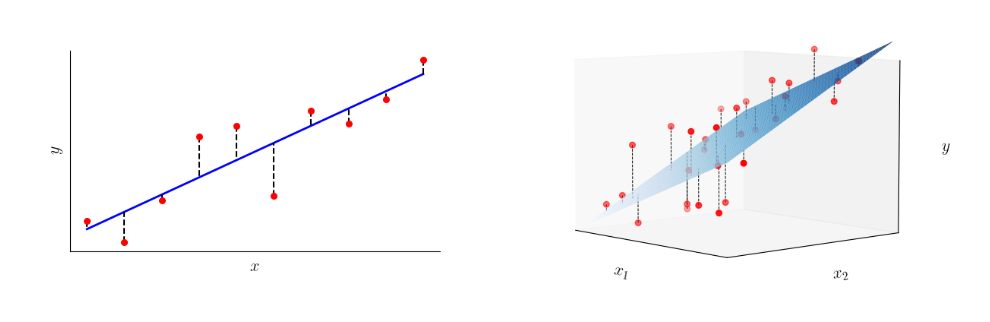
线性回归 是一种基本但极为重要的监督学习算法，广泛用于预测连续数值型数据。其主要目标是通过分析已知数据点之间的关系，找出一个能够用来预测新数据点的函数模型。在最简单的情况下，线性回归尝试找到一条直线，这条直线能够最佳地通过数据点，并最小化预测值与实际值之间的差异。

在线性回归模型中，我们通常假设因变量 $y$ 与自变量 $x$ 之间存在线性关系，这种关系可以用一个简单的数学公式表示为：

$\beta_0 + \beta_1x + \epsilon$

其中：

$y$ 是因变量（即我们想要预测的值）。
$x$ 是自变量（即我们用来预测 $y$ 的值）。
$\beta_0$ 是截距（当 $x = 0$ 时的 $y$ 值）。
$\beta_1$ 是斜率（表示 $x$ 每增加一个单位时， $y$ 的变化量）。
$\epsilon$ 是误差项（表示由于模型简化或其他未被观测到的因素所造成的偏差）。

二、线性回归的原理

线性回归的核心思想 是找到一组最优的模型参数 $\beta_0$ 和 $\beta_1$ ，使得模型的预测值与实际观测值之间的误差最小。这个过程通常通过最小化“残差平方和”（Sum of Squared Residuals, SSR）来实现。

图1 1 维和 2 维输入特征的线性模型

2.1 模型建立

首先，我们假设数据中的自变量 $x$ 和因变量 $y$ 之间存在一个线性关系，即：

$y_i = \beta_0 + \beta_1x_i + \epsilon_i$

其中， $i$ 表示数据点的索引， $\epsilon_i$ 是误差项。

2.2 残差和残差平方和

对于每个观测数据点 $i$ ，模型的预测值 $\hat{y}_i$ 与真实值 $y_i$ 之间的差异被称为残差（Residual），定义为：

$\text{残差} = y_i - \hat{y}_i$

为了评估模型的整体表现，我们计算所有残差的平方和，这个值被称为 残差平方和（Sum of Squared Residuals, SSR）：

$\sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = \sum_{i=1}^{n} (y_i - (\beta_0 + \beta_1x_i))^2$

2.3 最小二乘法

最小二乘法（Least Squares Method）是一种用来确定最优模型参数 $\beta_0$ 和 $\beta_1$ 的方法。其目标是找到参数值，使得残差平方和 $SSR$ 最小化。为了达到这一目标，我们需要对 $SSR$ 求导并找到其最小值。

首先，对 $\beta_0$ 和 $\beta_1$ 求偏导数：

$\frac{\partial SSR}{\partial \beta_0} = -2 \sum_{i=1}^{n} (y_i - \beta_0 - \beta_1x_i)$

$\frac{\partial SSR}{\partial \beta_1} = -2 \sum_{i=1}^{n} x_i(y_i - \beta_0 - \beta_1x_i)$

将这些偏导数设为零，可以得到以下两个方程：

$\sum_{i=1}^{n} (y_i - \beta_0 - \beta_1x_i) = 0$

$\sum_{i=1}^{n} x_i(y_i - \beta_0 - \beta_1x_i) = 0$

通过求解这两个方程，我们可以得到最优的 $\beta_0$ 和 $\beta_1$ 值：

$\beta_1 = \frac{n \sum_{i=1}^{n} x_i y_i - \sum_{i=1}^{n} x_i \sum_{i=1}^{n} y_i}{n \sum_{i=1}^{n} x_i^2 - (\sum_{i=1}^{n} x_i)^2}$

$\beta_0 = \frac{1}{n} \sum_{i=1}^{n} y_i - \beta_1 \frac{1}{n} \sum_{i=1}^{n} x_i$

这样一来，我们就找到了能够最佳拟合数据点的回归直线，即最优的 $\beta_0$ 和 $\beta_1$ 参数。

2.4 模型的评估

在得到模型后，我们需要评估其效果，常用的评估指标包括：

决定系数 $R^2$ ：衡量模型解释变量 $x$ 对因变量 $y$ 的解释能力，取值范围为 0 到 1，越接近 1 表明模型越好。
均方误差（MSE）：衡量模型预测值与实际值之间的平均误差平方。

三、案例分析：房价预测

我们将使用加州房价数据集（California Housing Dataset），这是一个公开的机器学习数据集，包含加利福尼亚州各地区的房屋信息，包括房价、中位数收入、住房年龄等特征。我们将通过房屋面积和中位数收入来预测房价。

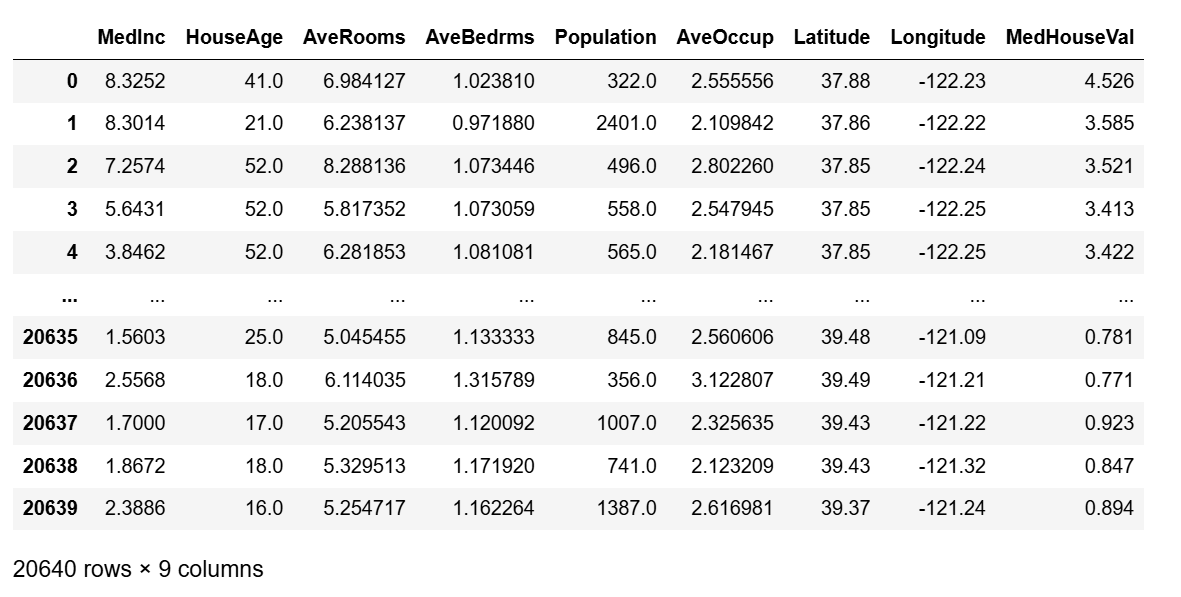
1. 导入数据集和必要的库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

# 设置字体，解决中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体字体显示中文
plt.rcParams['axes.unicode_minus'] = False  # 解决坐标轴负号显示问题

# 加载加州房价数据集
california = fetch_california_housing()
data = pd.DataFrame(california.data, columns=california.feature_names)
data['MedHouseVal'] = california.target
data

2. 创建和训练线性回归模型

# 选择特征 'MedInc' 进行建模
X = data[['MedInc', 'HouseAge', 'AveRooms', 'AveOccup']]
y = data['MedHouseVal']

# 分割数据为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 初始化线性回归模型
model = LinearRegression()

# 训练模型
model.fit(X_train, y_train)

3. 模型预测和评估

# 使用测试集进行预测
y_pred = model.predict(X_test)

# 评估模型表现
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print(f"均方误差（MSE）: {mse}")
print(f"决定系数（R^2）: {r2}")

均方误差（MSE）: 0.657451727882265

决定系数（R^2）: 0.49828508595474374

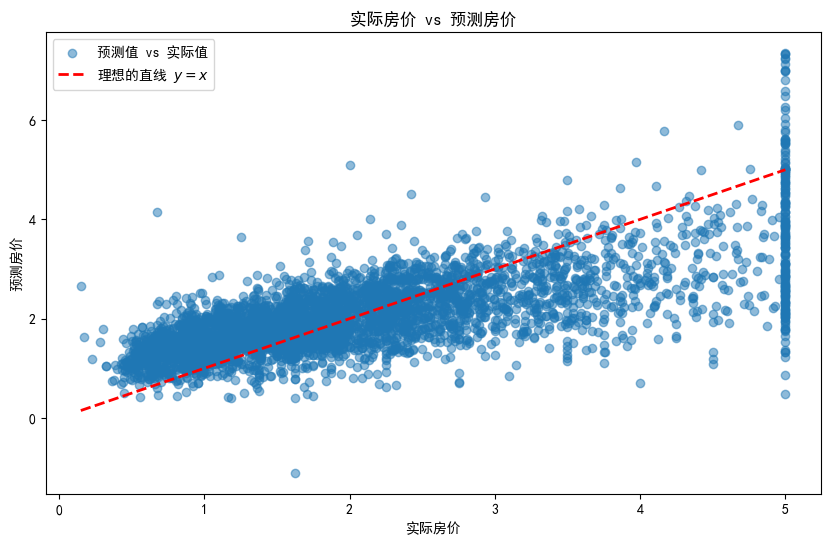
4. 结果展示

# 可视化预测值与实际值的比较
plt.figure(figsize=(10, 6))
plt.scatter(y_test, y_pred, alpha=0.5, label="预测值 vs 实际值")
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=2, label="理想的直线 $y = x$")
plt.xlabel("实际房价")
plt.ylabel("预测房价")
plt.title("实际房价 vs 预测房价")
plt.legend()
plt.show()